C1.2 Créer des suites à motif répété, des suites croissantes et des suites décroissantes comprenant des nombres rationnels, à l’aide d’une variété de représentations, y compris des expressions algébriques et des équations pour les suites croissantes et décroissantes linéaires, et établir des liens entre les différentes représentations.
Activité 1 : différentes représentations
Matériel :
- Papier quadrillé
- Crayons de couleur
À partir de l’équation c = 3r +2, l’élève sera responsable de répondre à une série de consignes. Il est important pour l’élève de pouvoir représenter les suites de différentes façons.
- Créez sur votre papier quadrillé une suite semi-concrète représentant l’équation du départ. Indiquez clairement le motif sur votre dessin. Assurez-vous d’avoir au moins 4 termes dans la suite.
- Représentez la suite dans une table de valeurs. Indiquez clairement la signification des variables utilisées.
- Tracez sa représentation graphique sur du papier quadrillé. Que remarquez-vous?
* Refaire l’activité pour une équation qui donne une suite décroissante.
Pour le retour, inviter les élèves à se regrouper en équipes afin qu’elles et ils puissent comparer leurs stratégies et réponses. Refaire la même chose en groupe-classe pour conclure.
Exemples de stratégies (disposition des carrés sur papier quadrillé)
Exemple 1
Représentation c = 3r + 2
c : nombre de carrés r : rang de la figure

Rang un : 2 carrés rouges superposés verticalement et 3 carrés verts. Superposés verticalement. Rang 2 : 2 carrés rouges superposés verticalement et 6 carrés verts. Superposés verticalement. Rang 3 : 2 carrés rouges superposés verticalement et 12 carrés verts superposés verticalement.
Exemple 2
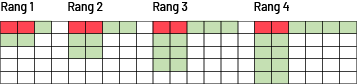
Rang un: 2 carrés rouges et 2 carrés verts en dessous des rouges et un carré vert à la droite des rouges. Rang 2: 2 carrés rouges et 4 carrés verts en dessous des rouges et 2 carrés verts à la droite des rouges. Rang 3: 2 carrés rouges et 6 carrés verts en dessous des rouges et 4 carrés verts à la droite des rouges.
Questions possibles
- Comparer les suites construites. Que remarquez-vous? Indiquez les similitudes, les différences.
- Est-ce que les règles obtenues sont identiques? Équivalentes?
Note : Lorsque simplifiées, les règles devraient être équivalentes à c = 3r+ 2.
Activité 2 : créons des suites non linéaires
Matériel : blocs, tuiles, feuilles quadrillées, logiciel traceur de courbe
Diviser les élèves en équipes. Écrire les consignes suivantes au tableau :
- Vous devez créer une suite non linéaire à l’aide du matériel à votre disposition.
- Vous devez représenter votre suite à l’aide d’une table de valeurs et d’une représentation graphique.
- Pour terminer, décrire pourquoi cette suite est non linéaire et décrire sa règle de régularité.
Faire un retour en groupe-classe. Demander à certaines équipes de présenter leur suite.
Activité 3 : une suite d’hexagones

Source : Guide d’enseignement efficace des mathématiques, de 7e à la 10e année, p. 40.
Projeter l'image ci-dessus au tableau. Les élèves doivent trouver une démarche afin de déterminer une équation pour calculer le périmètre, p, d’une chaîne de n hexagones.
Chaque équipe devrait avoir une table de valeurs indiquant le périmètre en fonction du nombre d’hexagones, et terminer avec une équation qui permet de trouver ce périmètre. Vous pouvez aussi leur demander de tracer la représentation graphique du périmètre en fonction du nombre d’hexagones.
Note : Pour les élèves ayant de la difficulté, donner des indices comment définir les variables à utiliser afin de trouver l’équation.
Faire un retour (il y a quelques possibilités) et comparer les stratégies et les réponses des élèves. Toutes les équations qui fonctionnent devraient se simplifier et donner la même équation et la même représentation graphique.
