B2.2 Recall and demonstrate addition facts for numbers up to 10, and related subtraction facts.
Skill: Recalling Addition Facts for Numbers up to 10 and Related Subtraction Facts
There are many strategies that can help students develop their arithmetic skills. Not all students use the full range of strategies; a few students use one, for example, the doubles strategy. Students abandon less effective strategies as they discover and create more effective ones.
In the primary division, students first use objects or their fingers to represent problems and then, building on these experiences, begin to use more advanced counting strategies.
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 6e année, p. 11-12.
Representation of Basic Number Facts
Using models to represent basic number facts can help students understand the meaning of basic operations and lessen their abstract nature. Many models can be developed using the materials below to build students' understanding of addition and subtraction:
- objects, such as tokens or tiles;
- visual material, such as illustrations;
- a five frame;
- a ten frame;
- meeting mats;
- two-coloured tiles;
- a number line;
- number grids.
The models help students make connections between drawings or pictures, symbols and words. Below are different models that can represent the basic 6 + 3 fact for students. Each of the four representations is appropriate. Note only that students will find it less necessary to use visual representations as they develop some automaticity in solving basic number facts.
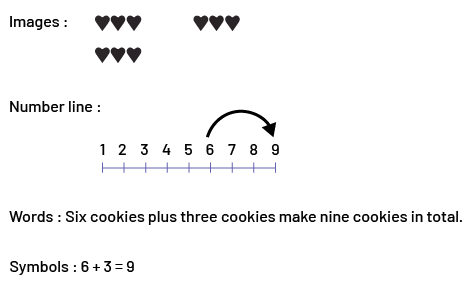
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 6e année, p. 15.
Strategies for Learning Basic Number Facts
Teachers can help students develop effective strategies for identifying basic number facts by using their reasoning and encouraging them to look for patterns and relationships among numbers. The basic number fact strategies described below build on knowledge that students already have to determine unknown facts. For example, knowing what 2 + 2 is helps students figure out what 2 + 3 is (since 3 is 1 more than 2, the answer must also be 1 more), indicating an important reasoning skill. Strategies should be taught in a problem-solving context. In this regard, one should:
- select problems that lend themselves to the use of the strategies taught;
- provide opportunities for students to model the strategy under study for themselves;
- have students practice the strategy in a meaningful context.
Students need many experiences to become familiar with grouping by tens and to establish relationships between the number 10 and other numbers before they can develop strategies for basic number facts. Recognizing the number 10 as an anchor and defining the relationships between this benchmark and the numbers 0-10 is a core concept for all students. A solid understanding of how numbers are related to 10 (for example, 8 is 2 less than 10) will enable them to discover patterns and relationships between numbers when presented with strategies focused on basic number facts. Knowing the ways in which numbers are related to each other will make it easier for them to learn strategies based on decomposing numbers.
A ten frame is an important tool that allows students to represent numbers from 0 to 10 concretely and gives them the opportunity to relate 10 to other numbers. When some of the boxes in the frame are filled in, it is possible to see the empty boxes and recognize the overall number represented. Students can work with a ten frame and tokens to illustrate numbers from 0 to 10 (a filled ten frame). Using different coloured tokens, students can identify relationships and see how they relate to the number 10 and different ways to break down the number 10. For example, if there are 8 blue tokens on one ten frame and 2 red tokens on another ten frame, students can grasp that 8 blue tokens plus 2 red tokens equals 10 tokens. Students can then concretely see the decomposition of the number 10 by changing the number of tokens of each colour by having a filled ten frame.
The strategies below are not presented in any particular order. Some students may find some strategies more useful than others, or may ignore some strategies in favour of their own. Others may find it easier to memorize facts than to rely on a strategy. Whatever the case, the teacher's primary goal is to get students to fully understand addition and subtraction.
1 More and 2 More
In the basic number facts 5 + 1 = 6, 5 + 2 = 7, 7 + 1 = 8, 7 + 2 = 9, one of the terms in each addition is 1 or 2. The strategy is based on the assumption that students easily remember the number that follows and the one that comes after.
Math Facts With 0 (1 + 0 = 1, 1 - 0 = 1)
In these basic number facts, 0 is one of the terms in each addition and subtraction. Students often overgeneralize by thinking that the answer to addition is necessarily larger and the answer to subtraction is necessarily smaller. Understanding of the concept of the identity property in addition and subtraction can be reinforced through games using flashcards and numbered cubes.
Use of Doubles
In these basic number facts, the first term and the second term (or both terms) are the same. It is beneficial for students to recognize and learn about doubles. There are only ten number facts related to doubles. Simple memorization tricks can be used to learn several doubles:
Double of 3: an insect has 3 legs on one side and 3 legs on the other (6).
Double of 4: a spider has 4 legs on one side and 4 legs on the other (8).
Double of 5: the 5 fingers of one hand and the 5 fingers of the other (10).
Double of 6: a box of a dozen eggs cut in half, 6 on one side and 6 on the other (12).
Double of 7: on the calendar, there are 7 days in a week and 14 days in two weeks.
Double of 8: There are 8 crayons in one row of a crayon box and 16 crayons in two rows.
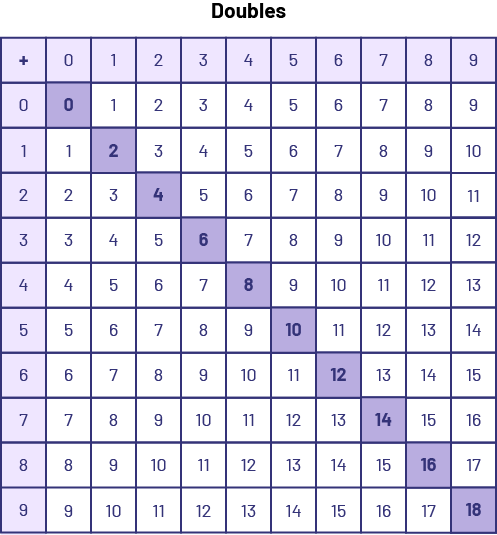
Neighbours of Doubles or Doubles Plus 1 (5 + 4 can be seen as 4 + 4, and 1 more)
In these basic number facts, one term of the addition is 1 more than the other term. Students can learn to recognize that in these additions, the answer is the same as the double of the lesser number plus 1 (5 + 4 = 4 + 4 + 1)). Students need to be proficient with doubles before they can use this strategy effectively.
Commutative Property (1 + 2 = 2 + 1)
Students who recognize the commutative property of addition can cut the amount of number facts they need to learn in half. Visual representation of facts such as 3 + 2 and 2 + 3 helps students grasp this relationship.
Subtraction as the Inverse Operation of Addition for Basic Math Facts with a Sum up to 10
Students who know their addition well and understand that subtraction is the inverse operation of addition can use this knowledge to master the related subtractions (if 5 + 2 = 7, it follows that 7 - 5 = 2). For example, consider the following problem: "Julian has 6 marbles in his bag. George gives him some more. Julian now has 10 marbles. How many marbles did George give to Julian? Faced with this problem, the student thinks: "What number added to 6 gives 10? Thus, the addition facts with which he is familiar help him to find the unknown term in the number sentence.
1 Less and 2 Less
These subtraction facts have one term of 1 or 2 less than the other term. Students can usually count backwards for the easiest number facts, such as any number from which 0, 1, or 2 is subtracted.
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 6e année, p. 14-20.