B1.7 Recognize that one half and two fourths of the same whole are equal, in fair-sharing contexts.
Activity 1: Which Game? (Represent Halves and Fourths)
Directions
Present an equal sharing scenario to the students. For example, four friends are sharing 12 carrot sticks. How many carrot sticks does each friend get?
Give 12 two-coloured counters to each student or pair of students.
Ask them to share the counters so that each student gets the same number and colour of counters.
Ask students the following questions:
- What does each of these equal groups represent? (3 carrots that each friend will get)
- How many carrots in all? (12)
- How many friends? (4)
- What part of the whole goes to each friend? (one-fourth)
- How many fourths are there? (4)
Now ask the students to flip the counters over for two of the groups to reveal the other colour.
Ask students the following questions:
- What does each of these equal groups represent now? (3 carrots that each friend will get)
- How many of the carrots are red? (6)
- How many of the carrots are white? (6)
- How many carrots in all? (12)
- What part of the whole is red carrots? (half)
- What part of the whole is white carrots? (half)
- How many halves are there? (2)
- How many fourths are in a half? (2)
Note: To recognize the different groups, write the name of the fraction in words (for example, a fourth). It is important that students associate the name of the fraction (for example, a fourth) with the number of groups or parts.
Source: inspired by Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, Numération et sens du nombre, p. 54.
Activity 2: Making Bracelets and Rings
To create beautiful bracelets and rings, four students share six strings. How many pieces of string will each student get? What do you notice?
Sample Solutions
Use a Length Model (Relational Rods) to Represent Equivalent Fractions
I choose the rods to represent the 6 strings. Since I have to divide these strings between 4 students, I divide these 6 strings into 4 equal parts using the unit cubes. I can assign a whole purple rod to each student. Each purple rod represents 1 unit or 4 one-fourths.
I have two purple rods left. I divide the two purple rods equally into 4 equal parts, one part for each student. These equal red parts are each one-half or 2 one-fourths.
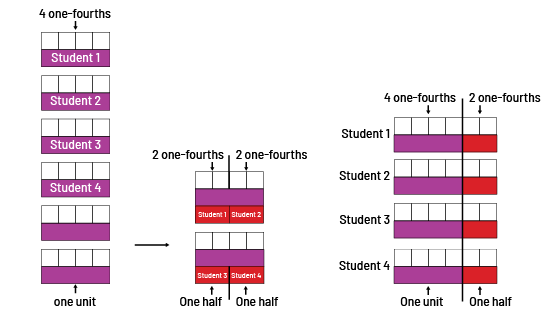
Each student is given 1 and a half strings, 1 string and two-fourths or 6 fourths to create bracelets and rings.
Source: translated from En avant, les maths! ML, Nombres, p. 6.
