B2.5 Represent and solve problems involving the multiplication of two- or three-digit whole numbers by one-digit whole numbers, and by 10, 100, and 1000, using appropriate tools, including arrays.
Activity 1: Multiply by 10, 100 and 1000
Have students solve the following problems:
- Patrick says that \(5 \times 100\) is equal to \(50 \times 10\). Is he right? Explain your answer.
- Nicole says that \(6 \times 1000\) is equal to \(60 \times 100\). Is she right? Explain your answer.
- A number is a multiple of 100, but it is not a multiple of 10. Is this possible? Explain your answer.
Source: translated from Les mathématiques...un peu, beaucoup, à la folie!, Guide pédagogique, Numération et sens du nombre 4e, Module 2, série 2, p. 206.
Activity 2: Problems to Solve
Provide students with a variety of problems to solve, including:
Equal Groups Problem (multiplication) and Combining Problem
The children had fun tracing shapes on the sidewalk. They drew 5 triangles, 7 rectangles and 3 hexagons. How many sides did they draw if the shapes did not touch each other?
Combinations Problem
Suzie is packing her suitcase. She brings 4 sweaters and 3 pairs of pants. How many different outfits can she wear?
Equal Groups Problem (multiplication) and Comparison Problem (subtraction)
Corinne wants to put 2 stickers on each page of her album. Her album has 27 pages. She has 5 packages of 12 stickers. Does she have enough stickers?
Equal Groups Problem (multiplication)
Jacob has 3 dimes and 9 nickels. How much money does he have?
Equal Groups Problem (multiplication)
How many seconds do you spend at school each day? How many seconds do you spend in a week at school?
Equal Groups Problem (multiplication)
The student council is planning a downhill ski trip. There are 24 students participating and the cost is $48 each. How much will this trip cost?
Equal Groups Problem (multiplication and division in the sense of "grouping")
We need to make sandwiches for a potluck dinner. How many sandwiches can be made with 3 loaves of bread containing 19 slices each?
Equal Groups Problem (multiplication and division in the sense of "sharing")
Four children had 3 bags of granola bars. They opened the 3 bags and decided to divide them equally between them. There are 52 granola bars in each bag. How many bars did each child get?
Equal Groups Problem (multiplication), Join Problem (addition) and Comparison Problem (subtraction)
At Sunset School, there are five Grade 3 classes. Four classes have 26 students and one has 27 students. In March, the Grade 3 students went to the museum. The teachers counted 109 students on the buses. How many students were absent?
Equal Groups Problem (multiplication) and Comparison Problem (subtraction)
Emily has 45 quarters in her money bank. She wants to buy a soccer ball for $10 (including taxes). Does she have enough money?
Multiplicative Comparison Problem
Justin did 6 times as many jumps as his little brother. His little brother did 4 jumps. How many jumps did Justin do?
Source: translated from L'@telier - Ressources pédagogiques en ligne (atelier.on.ca).
Activity 3: The Largest Product
Material
a die
Roll the die 4 times.
Write the 4 numbers on a piece of paper. Create a multiplication problem that will have the largest possible product.
Examples
If I roll 2, 5, 6, 1, which multiplication will have the greatest product? \(2\; \times \;651\;{\rm{or}}\;{\rm{216}}\; \times \;{\rm{5}}\).
If I roll 3, 3, 3, 4, which multiplication will have the greatest product? \(4\; \times \;333\;{\rm{or}}\;{\rm{3}}\; \times \;{\rm{433}}\).
Variations:
- Find the smallest product.
- Roll the die 5 times.
- Use a spinner numbered 0 to 9.
Source: translated from L'@telier - Ressources pédagogiques en ligne (atelier.on.ca).
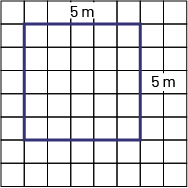
Activity 4: Multiplying With an Array
The school is preparing a "four corners" game in the playground. The dimensions of the field are 5 m by 5 m. What is the area of the playground?