GEEM - Skills and Knowledge

B2.1 Use the properties of operations, and the relationships between operations, to solve problems involving whole numbers and decimal numbers, including those requiring more than one operation, and check calculations.

Skill: Using the Properties of Operations

Understanding the properties of operations and the relationships between them supports for more flexible use of operations.

A good operation sense is based on a good knowledge of the relationships between numbers and between operations. Properties of operations are characteristics that are specific to operations, regardless of the numbers involved; as an example, addition is commutative since $3 + 5 = 5 + 3$ ; $4 + 7 = 7 + 4$ ; $1.22 + 3.51 = 3.51 + 1.22$ .

Understanding the properties of the operations allows one to develop efficient computational strategies; for example, since multiplication is distributive over addition, one can compute $5 \times 12$ by performing $(5 \times 10) + (5 \times 2)$ .

In the primary grades, students have been able to approach some of these properties intuitively. Junior students need to understand the properties of the operations presented below and learn to use them in problem solving situations.

Commutative Property

Addition and multiplication are commutative. For example, the commutative property of addition can be demonstrated as follows: there are 44 apples in one basket and 32 in another. The total number of apples will be the same whether we add the apples in the first basket to the apples in the second basket or we do the opposite. Thus, $44 + 32$ and $32 + 44$ are both equal to 76. Students should recognize that if the order of the terms of an addition are switched, the result remains the same.

We can also demonstrate the commutative property of multiplication. For example, $8 \times 3$ and $3 \times 8$ .

And $8 \times 3.5$ and $3.5 \times 8$

The two previous arrays represent the same total quantity, organized in two different ways. As a result, they illustrate two different situations. Thus, $8 \times 3$ represents 8 rows of 3 objects and $8 \times 3.5$ represents 8 rows of 3.5 objects, while $3 \times 8$ represents 3 rows of 8 objects and $3.5 \times 8$ represents 3.5 rows of 8 objects. It is important that students recognize the different representations.

An example from everyday life can also be used to illustrate this concept. For example, invite three students who have exactly one sibling to come and represent the number of children in their family in a diagram on the board. The total number of children, 6, is represented by children. (Figure 1).

Then, do the same with two children who have exactly two siblings. The total number of children, 6, is represented by children. (Figure 2).

Figure 1

Figure 2

The two number sentences, $3 \times 2 = 6$ and $2 \times 3 = 6$ , indicate the same result, even if the order of the factors is reversed. The students can then understand that three families with two children or two families with three children have the same total of six children, even though the situations are not identical.

When we use the commutative property of multiplication, we are more interested in the answer than the situation.

For example, even if we are looking for the answer to $12 \times 2$ , we can choose to calculate $2 \times 12$ if it is easier for us.

When first learning multiplication, students often think of multiplication as repeated addition. As they attempt to solve a variety of problems, they can use the commutative property of multiplication to develop a more efficient strategy for calculation.

For example, students using repeated addition would recognize that $2 \times 12$ is the same as two 12s or 12 + 12 and is simpler and takes less time to represent and calculate than $2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2$ .

An array is an excellent visual model for representing the commutative property of multiplication.

Associative Property

In the expression $15 + 13 + 17$ , it is possible to associate 13 and 17 to make $15 + (13 + 17)$ , which gives $15 + 30$ , or 45. We can also associate 15 and 13 to make $(15 + 13) + 17$ , which gives $28 + 17$ , or 45. The associative property also applies to decimal numbers. For the expression $5 + 0.75 + 0.25$ , it is possible to associate 0.75 and 0.25 to make $5 + (0.75 + 0.25)$ , which gives $5 + 1$ , or 6. We can also associate 5 and 0.75 to make $(5 + 0.75) + 0.25$ , which makes $5.75 + 0.25$ , or 6.

The associative property of multiplication [for example, $3 \times 2 \times 5$ is equal to $3 \times (2 \times 5)$ or $(3 \times 2) \times 5$ ] is not easy to understand. Certainly, it can be seen by checking the results of each expression, but this does not constitute an understanding. To understand, one can use an extension of the array model with the help of cubes.

In Figure 1, we see that there are 2 rows of 5 cubes, that is, $2 \times 5$ cubes. In Figure 2, we see 3 layers of $2 \times 5$ cubes representing $3 \times (2 \times 5)$ cubes.

One can also consider Figure 3, which illustrates 3 layers of 2 cubes, or $3 \times 2$ cubes. Figure 4 can then represent these cubes iterated 5 times, which is represented as $(3 \times 2) \times 5$ .

The associative property does not change the order of numbers in a numerical expression. We can see that $3 \times (2 \times 5)$ and $(3 \times 2) \times 5$ represent the same amount of cubes (even though each expression represents a different configuration) and that each gives the same product as $3 \times 2 \times 5$ .

Faced with a numerical expression such as $3 \times (2 \times 5) = ?$ , some students try to apply the distributive property in such a way that they calculate $(3 \times 2) \times (3 \times 5)$ , which has the effect that $2; \times 5$ is multiplied by 9, rather than by 3. In such a case, remember that the distributive property says that multiplication is distributed over addition or subtraction and explain the situation using a concrete or visual (semi-concrete) model.

The associative property and the commutative property can be combined to facilitate the evaluation of a numerical expression.

For example, to determine the value of the expression $2 \times 3 \times 5$ , one can first use the commutative property to make $2 \times 5 \times 3$ which allows us to associate the 2 and the 5, then determine that of the expression $(2 \times 5) \times 3$ . It is usually easier to calculate $10 \times 3$ than to calculate $6 \times 5$ . Similarly, to determine the value of the expression $19 + 27 + 11$ , one can determine that of $(19 + 11) + 27$ , because the 9 and the 1 are complementary and make 1 ten, the answer can more likely be obtained mentally as $30 + 27 = 57$ . By exposing students to a large number of activities, teachers can support students to understand and use the different properties effectively.

Decomposing a number into a product of factors, along with the associative property, can also be useful. For example, the number 24 can be represented by $24 \times 1, 12 \times 2, 8 \times 3, 6 \times 4$ or even by $2 \times 4 \times 3$ or $2 \times 2 \times 2 \times 3$ . To determine the value of a numeric expression such as $24 \times 5$ , students with good number and operation sense may choose to transform 24 into $12 \times 2$ and use the operations properties as follows:

\begin{array}{l} 24 \times 5 = (12 \times 2) \times 5 \\ 24 \times 5 = 12 \times 2 \times 5 \\ 24 \times 5 = 12 \times 10 \\ 24 \times 5 = 120 \end{array}

\begin{array}{l} 24 \times 5 = (12 \times 2) \times 5 \\ 24 \times 5 = 12 \times 5 \times 2 \\ 24 \times 5 = 60 \times 2 \\ 24 \times 5 = 120 \end{array}

Distributive Property

Multiplication is distributive over addition. For example, we can multiply $3 \times (5 + 6)$ and arrive at the same result as if we had performed $(3 \times 5) + (3 \times 6)$ . Multiplication is also distributive over subtraction. For example, we can multiply $3 \times (20 - 2)$ by doing $(3 \times 20) - (3 \times 2)$ .

The following example illustrates how the distributive property can be used to calculate $6 \times 8$ . In one case, we decompose the factor 8 to obtain $5 + 3$ . We then have $6 \times (5 + 3) = (6 \times 5) + (6 \times 3)$ . In the other case, we decompose the factor 6 to obtain $3 + 3$ . We then have $(3 + 3) \times 8 = (3 \times 8) + (3 \times 8)$ .

The distributive property can be used when making a calculation involving decimal numbers, such as $6.5 \times 4$ .

Here, we can decompose the factor 4 to make $2 + 2$ . We then have $6.5 \times (2 + 2) = (6.5 \times 2) + (6.5 \times 2)$ . We can also decompose the factor 6.5 to make $6 + 0.5$ . We then have $(6 + 0.5) \times 4 = (6 \times 4) + (0.5 \times 4)$ .

There is an important connection between the distributive property and the standard multiplication algorithm. For example, to calculate $3 \times 15$ , the 15 is broken down to get $(10 + 5)$ :

In the case of $13 \times 24$ , both factors are decomposed:

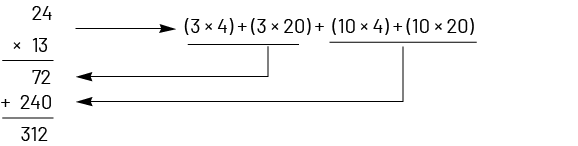
Only multiplication is distributive over addition or subtraction. However, division is partially distributive. For example, to calculate $32 \div 8$ , it is possible to decompose the dividend 32 into $16 + 16$ . We then have $(16 + 16) \div 8$ and the division by 8 is distributed over the addition. We get $(16 \div 8) + (16 \div 8) = 2 + 2$ , which is, 4. However if the divisor is decomposed, the distributive property does not work. For example, $32 \div 8 \neq (32 \div 4) + (32 \div 4)$ showing that distributivity is not a property of division.

Source: translated from Guide d'enseignement efficace des mathématiques de la 4^e à la 6^e année, Numération et sens du nombre, Fascicule 1, Nombres naturels, p. 102-105.

Properties of operations can be used to verify an answer. For example, $4 \times 9$ can first be determined using the distributive property, $2 \times 9 + 2 \times 9$ or by decomposing $4 \times 9$ into $2 \times 2 \times 9$ and using the associative property to get $2 \times (2 \times 9)$ .

Source: adapted from Ontario Curriculum, Mathematics Curriculum, Grades 1-8, 2020, Ontario Ministry of Education.

Skill: Using the Relationships Between Addition, Subtraction, Multiplication and Division

Understanding the relationships between operations allows them to be used more flexibly.

The more opportunities students have to handle operations, the more they can notice and understand the relationships between them. Students may even use addition or subtraction strategies to solve multiplication and division.

In the Primary Division, students have made connections between operations through various activities. For example, they know that addition and subtraction are inverse operations and that addition is commutative. Over time, they develop their number sense and operation sense and gradually use them before performing operations. This practice, while often informal and mental, is still essential to understanding the relationships between numbers and between operations.

Source: translated from Guide d’enseignement efficace des mathématiques de la 4^e à la 6^e année, Numération et sens du nombre, Fascicule 1, Nombres naturels, p. 97.

Addition and Subtraction

Addition and subtraction are inverse operations. Any subtraction situation can be considered as an addition situation (for example, 154 - 48 = ? is equivalent to 48 + ? = 154) and vice versa.

However, students often have difficulty solving equations such as 17 + Δ= 31 when they are learning. Many teachers encourage their students to use the inverse operation, subtraction. However, this can be a learning trick unless students understand why subtraction is a possible strategy. They must first grasp the relationship of the whole to its parts and the meaning of "difference".

For example, a number can be represented as follows:

This way of representing the relationship between a number and its parts allows us to see that subtraction is the inverse operation of addition.

Since $17 + 14 = 31 a n d 14 + 17 = 31$ , then $31 - 17 = 14 a n d 31 - 14 = 17$ . Additionally, students can see why addition is commutative $(14 + 17 = 17 + 14 = 31)$ and why subtraction is not commutative $(31 - 17 \neq 17 - 31)$ . Those who have acquired good number sense and are able to break down and regroup numbers can use their knowledge to more effectively solve equations such as $17 + Δ = 31$ understanding that we are looking for the difference between 17 and 31.

Source: translated from Guide d'enseignement efficace des mathématiques de la 4^e à la 6^e année, Numération et sens du nombre, Fascicule 1, Nombres naturels, p. 97-98.

It is also possible to represent decimal numbers as follows:

We can also use addition to perform a subtraction; this strategy is called "adding to subtract". For example, to solve $31 - 17 = ?$ , the student can add from 17 onward to 31, or $17 + ? = 31$ .

This inverse relationship can be used to perform and verify calculations.

Multiplication and Division

Multiplication and division are also inverse operations. They can also be related to the concept of the whole and its parts. In multiplication, we group the equal groups, while in division, we partition a whole into equal groups. From this relationship between multiplication and division, students can use multiplication facts to perform division. Students often misunderstand the inverse operation relationship between multiplication and division (for example, recognizing that $? \times 6 = 234$ can be thought of as $234 \div 6 = ?$ even after performing divisions and checking their calculations. It is therefore essential to regularly review the meaning of each of the operations in the context of problem solving.

Source: translated from Guide d’enseignement efficace des mathématiques de la 4^e à la 6^e année, Numération et sens du nombre, Fascicule 1, Nombres naturels, p. 98.

Multiplication represents the result of gathering equal groups of objects together while division represents the division of objects into equal groups. To understand multiplication and division, one must recognize the three types of quantities involved: the total quantity (for example, 8 flowers), the number of equal groups (for example, 4 pots), and the size of each group (for example, 2 flowers per pot).

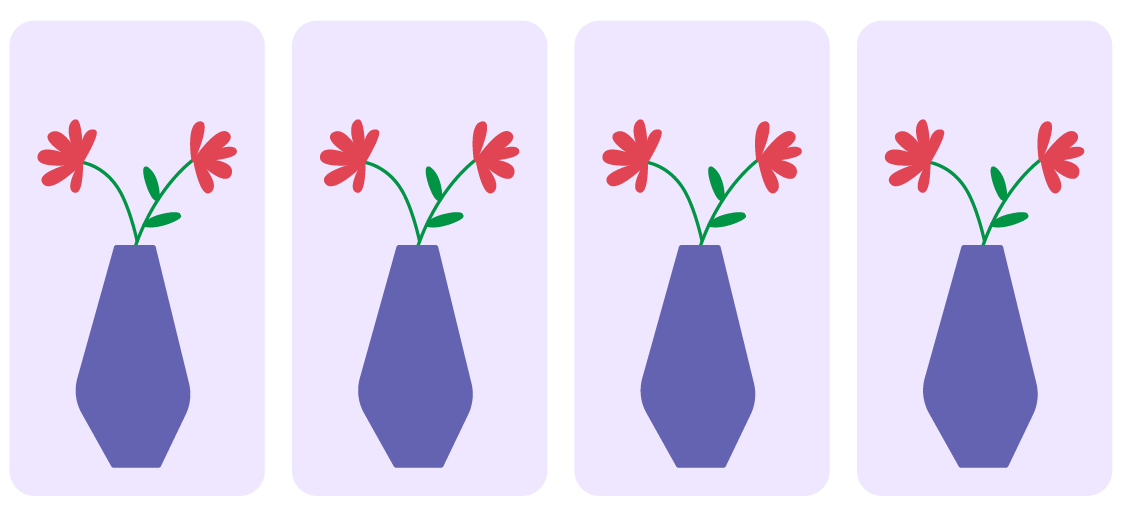
In the problems presented to students, division is too often associated with only one type, which is equal sharing. Equal grouping is usually neglected. Division has a partitive or sharing meaning when the total quantity and the number of groups are known (for example, 3 students want to share 15 apples equally and we want to find the number of apples each will receive).

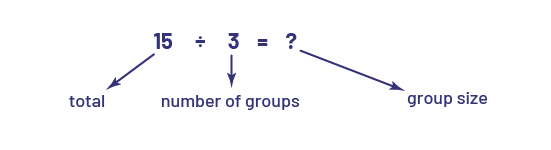
Division has a quotative measurement or grouping meaning when the total quantity and the number of items in each group (group size) are known (for example, we have 15 apples and want to put them in bags of 3; we want to find the number of bags we need).

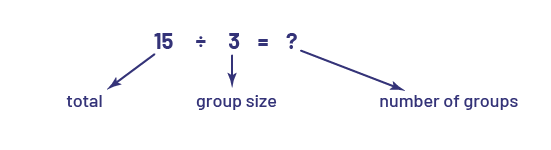
It is essential that both types of situations be addressed, as they are the basis for the integration of other mathematical concepts. It is not necessary for students to know the names of the situation types, but it is essential that they have the opportunity to solve a variety of problem types, while using a variety of strategies.

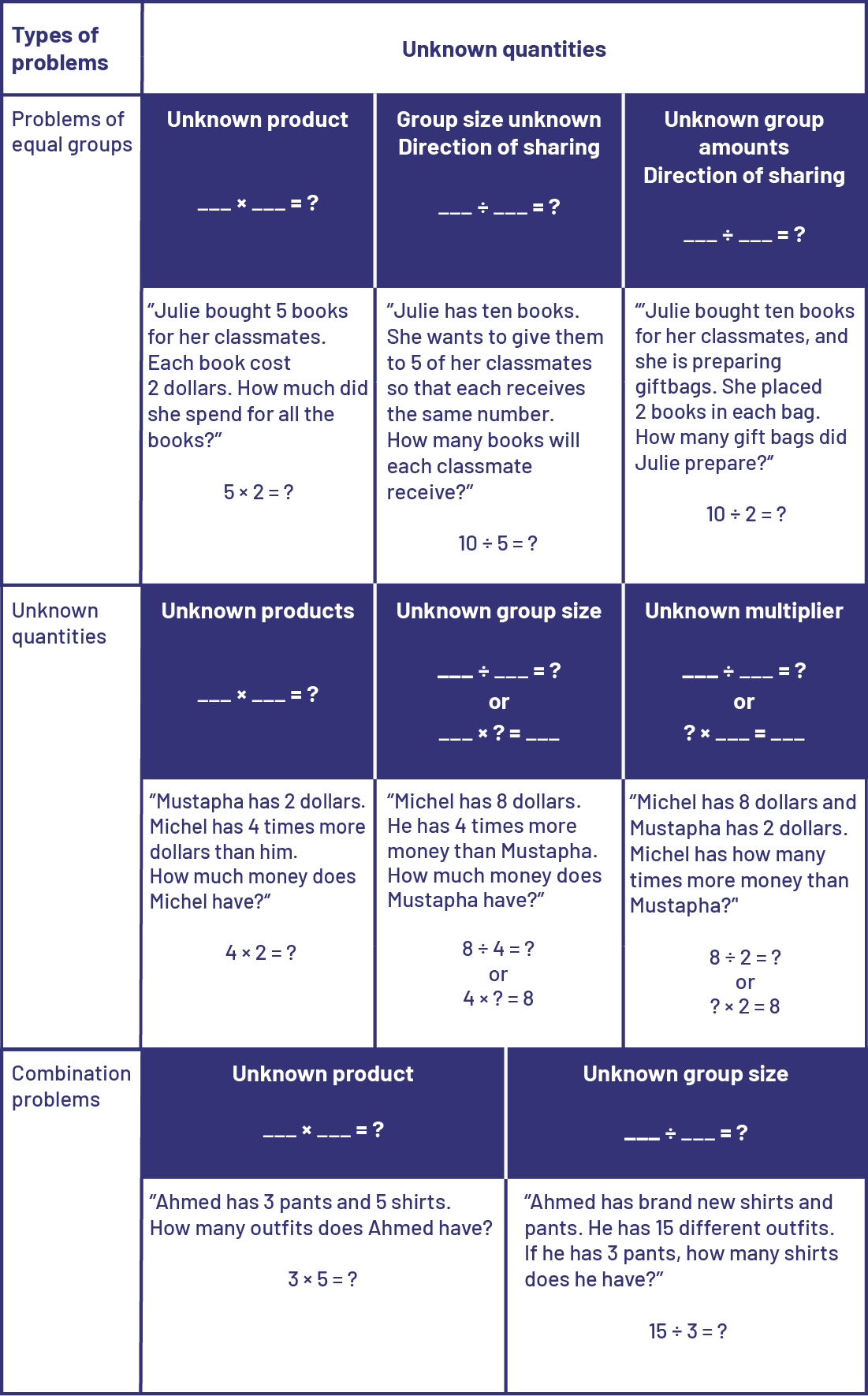
Source: translated from Guide d'enseignement efficace des mathématiques de la 4^e à la 6^e année, Numération et sens du nombre, Fascicule 1, Nombres naturels, p. 84-86.

Multiplication and Addition

The connection between multiplication and addition is often the starting point for introducing the concept of multiplication.

In the early stages of learning multiplication, students recognize when a situation presents the same quantity many times, and they use equal groups to represent the situation and repeated addition to get an answer. As students progress, it is important that they see the concept as multiplication rather than addition and learn other representations. The array, a row and column arrangement, is a powerful model for learning multiplication and provides a different perspective on multiplication.

Through solving a variety of problems and discussing strategies, students come to establish and grasp the connection between the word "times" and the "×" sign, a crucial step in developing an understanding of multiplication. Once their sense of multiplication is well established, they use the multiplication operation more regularly to obtain answers.

Source: translated from Guide d'enseignement efficace des mathématiques de la 4^e à la 6^e année, Numération et sens du nombre, Fascicule 1, Nombres naturels, p. 85-86.

Division and Subtraction

Similarly, division can be associated with repeated subtraction, but not in the same way. The product of a multiplication is equal to the sum resulting from the repeated addition, while the quotient of a division is equal to the number of repeated subtractions (for example, to calculate $20 \div 5$ , we do $20 - 5 = 15, 15 - 5 = 10, 10 - 5 = 5, 5 - 5 = 0$ ; we subtracted 4 times; therefore $20 \div 5 = 4$ ).

It takes time for students to learn these relationships. To achieve this, teachers can use hands-on activities, problem solving, and mathematical discussions that focus on the connections between operations.

Source: translated from Guide d'enseignement efficace des mathématiques de la 4^e à la 6^e année, Numération et sens du nombre, Fascicule 1, Nombres naturels, p. 98-99.

Impact of the Mathematical Operations

Each operation has an effect on the quantities involved. Depending on the operation, certain quantities increase or decrease. They can increase or decrease by a lot or a little.

Tracking the effect of operations on numbers allows students to make connections between operations and to anticipate the outcome of an operation. For example, if we subtract 8 from 160, we will notice little effect because the difference between 160 and 152 is relatively small. However, if we divide 160 by 8, the effect is large, because the resulting quotient, 20, is much smaller than 160. We can also compare the effect produced by addition to that produced by multiplication.

Compared to multiplication, addition increases a number by a small amount. For example, when the number 160 is multiplied by 8, you get 1280, whereas if you add 8 to it, you get only 168. People with good operations sense recognize the effect of operations on whole numbers, but students who are still learning are often impressed by the effect of, for example, multiplication.

One caveat is that care must be taken when generalizing, as operations on decimal numbers or fractions may have different effects than those on whole numbers.

In some cases, the effect can even be the opposite. If we multiply a whole number by another whole number, the product is greater than each of two factors (for example, if we multiply 3 by 6, the product 18 is greater than 6 and 3), whereas if we multiply a proper fraction by a whole number, the product is smaller than one of the two factors (for example, if we multiply $\frac{1}{2}$ by 6, the product one half as large as 6).

Source: translated from Guide d'enseignement efficace des mathématiques de la 4^e à la 6^e année, Numération et sens du nombre, Fascicule 1, Nombres naturels, p. 90-91.

Explore these ideas with students, having them uncover the effect of the operations. Have students work in pairs to observe the effects of the operations on the numbers, such as:

$\begin{array}{l} 160 + 8 \\ 160 - 8 \\ 160 \times 8 \\ 160 \div 8 \end{array}$

Students can use models, such as the number line to show operations.

Facilitate a mathematical discussion to bring out the effects of the different operations.

Knowledge: Properties of Operations

A property of an operation is a characteristic specific to that operation, regardless of the numbers involved.

Source: translated from Guide d'enseignement efficace des mathématiques de la 4^e à la 6^e année, Numération et sens du nombre, Fascicule 1, Nombres naturels, p. 102.

The properties of the operations are:

Commutative Property: $(3 + 5 = 5 + 3)$ and $3 \times 5 = (5 \times 3)$
Associative Property: $(2 + 9) + 11 = 2 + (9 + 11)$ and $(2 \times 9) \times 5 = 2 \times (9 \times 5)$ ;
Distributive Property: $8 \times 7 = (8 \times 5) + (8 \times 2)$ ;
Identity Principle of Multiplication: $25 \times 1 = 25$
Zero Property of Addition and Subtraction: $13 + 0 = 13$ $13 - 0 = 13$
Zero Property of Multiplication: $8 \times 0 = 0$

Knowledge: Commutative Property

An operation is commutative if its result remains unchanged when the order of its terms or factors is reversed. Addition and multiplication are commutative. For example, $27 + 63 = 63 + 27$ and $8 \times 6 = 6 \times 8$ .

Source: translated from Guide d'enseignement efficace des mathématiques de la 4^e à la 6^e année, Numération et sens du nombre, Fascicule 1, Nombres naturels, p. 102.

Knowledge: Associative Property

The associative property of addition and multiplication allows you to associate the terms or factors of an expression in different ways without changing the value of the expression. For example, $3 \times 2 \times 5 = 3 \times (2 \times 5)$ .

Source: translated from Guide d'enseignement efficace des mathématiques de la 4^e à la 6^e année, Numération et sens du nombre, Fascicule 1, Nombres naturels, p. 105.

Knowledge: Distributive Property

Multiplication is distributive over addition and subtraction.

The distributive property allows you to perform an operation on a sum or a difference of terms and obtain the same result as if the operation had been performed on each term. For example,

we can multiply $3 \times (5 + 6)$ by doing $(3 \times 5) + (3 \times 6)$ ;
we can multiply $3 \times (20 - 2)$ by doing $(3 \times 20) - (3 \times 2)$ .

Source: translated and based on Guide d’enseignement efficace des mathématiques de la 4^e à la 6^e année, Numération et sens du nombre, Fascicule 1, Nombres naturels, p. 104.

Knowledge: Zero Property of Multiplication

When multiplying any number by 0, the result is always 0 (for example, $684 \times 0 = 0 and 16.67 \times 0 = 0$ ).

Source: translated from Guide d’enseignement efficace des mathématiques de la 4^e à la 6^e année,Numération et sens du nombre, Fascicule 1, Nombres naturels, p. 107.

Knowledge: Identity Principle of Addition and Identity Principle of Multiplication

The Identity Principle of Addition states that when adding 0 to any amount, the amount stays the same (for example, $287 + 0 = 287$ and $4.5 + 0 = 4.5$ . The Identity Principle of Multiplication states that when multiplying an amount by 1, the amount stays the same (for example, $133 \times 1 = 133$ ; $432.1 \times 1 = 432.1$ .

There is no identity principle for either subtraction or division In subtraction, however, there is a Zero Principle which states that 0 subtracted from any number results in the same number, that is, n – 0 = n. Note: The number 0 has no effect when it is the 2nd term, such as for $3 - 0 = 3$ ), but this is not the case if it appears as the first term, such as for $0 - 3 \neq 3$ ). The specific wording of the principle, along with the knowledge that subtraction is not a commutative operation, should be emphasized with students. Similarly, the Identity Principle states that when dividing an amount by 1, the amount stays the same (for example, 3 ÷ 1 = 3). The number 1 has no effect when it is the divisor. Again, we must make clear to students that since division is not a commutative operation, we cannot then assume that the number 1 has no effect when it is the dividend (for example, dividing 3 by 1 results in 3, but dividing 1 by 3 does not result in 3).

Source: translated from Guide d’enseignement efficace des mathématiques de la 4^e à la 6^e année, Numération et sens du nombre, Fascicule 1, Nombres naturels, p. 107.

Knowledge: Relationships Between Addition, Subtraction, Multiplication and Division

The fundamental operations of addition, subtraction, multiplication and division are closely related despite their apparent differences.

Addition and subtraction are inverse operations.
Multiplication and division are inverse operations.
Multiplication can be associated with repeated addition.
Division can be associated with repeated subtraction.