B2.6 Represent and solve problems involving the multiplication of two-digit whole numbers by two-digit whole numbers using the area model and using algorithms, and make connections between the two methods.
Skill: Solving Problems Involving Multiplication of Two-Digit Whole Numbers by Two-Digit Whole Numbers
When solving problems, students are encouraged to use knowledge already acquired and to make connections to new learning. These connections can be broken if students are not presented with a diverse range of problems. Students who do not learn to perform calculations within problem-solving contexts may have great difficulty making these connections later. Their understanding of the abstract concept of number and its application may be blurred, and some may not be able to use computational strategies effectively to solve problems.
The use of problem-solving contexts is equally important for operations on multi-digit numbers. When students are given problems, when they are encouraged to develop an algorithm and use it flexibly, they are given the opportunity to deepen their understanding of operations. For the sake of efficiency and believing we are doing the right thing, teachers often teach an algorithm to be used to perform operations on multi-digit numbers. When a method presented to students as "the right way" to solve the problem, they make arduous efforts to understand and memorize this procedure. This often results in inefficient use of the algorithm, lack of accuracy, and limited understanding. If, on the other hand, students are encouraged to identify the meaning of a problem and to develop their own strategies to solve it, they will demonstrate more ease and more precision in their work on operations.
Source: translated from Guide d'enseignement efficace des mathématiques de la maternelle à la 6e année, Fascicule 5, p. 5.
Types of Multiplication Problems
Students develop an understanding of multiplication and number relationships by solving problems of various types.
The types of problems presented below with examples can help students see the operations of multiplication and division in a variety of ways, depending on whether they are equal group or comparison problems. The use of these different types of problems promotes students to reason their way to solutions and thus helps develop a better sense of operations.
Source: translated from Guide d'enseignement efficace des mathématiques de la maternelle à la 6e année, Fascicule 5, p. 8.
The sample written problems below contain 2 or 3 digit numbers times a 1-digit number. The structures of both types of written problems also lend themselves to numbers having more digits.
Equal Group Problem
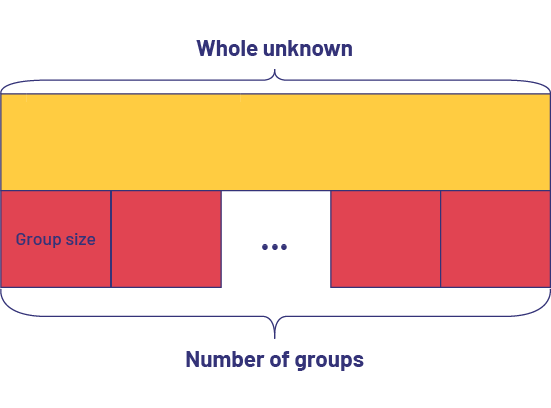
- Equal Groups: Whole (Product) Unknown (Multiplication)
The school purchased 150 books for the classes. Each one cost $5. How much did the school spend on all these books?

Decomposition of the First Factor and Distributive Property
\(\begin{align} 150 \times \;\$5\; &= (100 \times 5 ) + (50 \times 5 ) \\ &= 500 + 250 \\ &= \$750\; \end {align}\)
The school spent $750 on all of these books.
Comparison Problem
Representing the situation with relational rods or the number line helps determine the result.
- Comparison: Product Unknown
Mustapha has saved $20 in the last month. For his part, Michel saved 4 times more. How much money did Michel save?
\(4 \times \$20 = ?\)

\(\begin{align} 4 \times \$20\; &= 20 + 20 + 20 + 20 \\ &= \$80\; \end{align}\)
Michel saved $80.
Source: adapted and translated from Guide d'enseignement efficace des mathématiques de la maternelle à la 6e année, Fascicule 5, p. 10-11.
In the early stages of learning multiplication, students recognize that the situation presents the same quantity "many times" and they use equal groups to represent the situation and repeated addition to get the answer. As students progress, it is important that they begin to see multiplication as more than repeated addition and learn other representations.
The array, an arrangement of rows and columns, is a powerful model for learning multiplication and provides a different perspective on the operation.
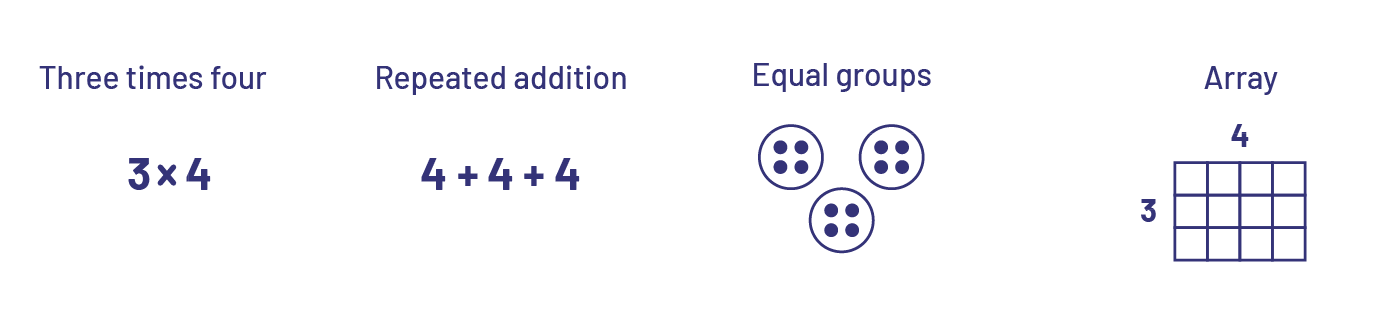
Through solving a variety of problems and discussing strategies, students come to establish and grasp the connection between the word "times" and the "×" sign, a crucial step in developing an understanding of multiplication. Students need to understand that the "×" sign can mean "groups of".
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 1, Nombres naturels, p. 85-86.
The array model can be introduced to students in a variety of ways. For example, teachers can use a student's work as a starting point and propose organizing objects into an array.
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 1, Nombres naturels, p. 134.
In a multiplication situation the number of rows and the number of columns for the array are both known. In a division situation the total number of objects is known, as well as either the number of rows or the number of columns. In order to create an array to represent a division situation, the objects are arranged into the rows or columns that are known until all the objects have been distributed evenly.
Source: Ontario Curriculum, Mathematics Curriculum, Grades 1-8, 2020, Ontario Ministry of Education.
Example
In the gymnasium, 12 rows of 15 chairs each are placed for a show. How many chairs are there altogether?

The array allows for visualization by representing each of the chairs. Students can then use repeated addition and count in increments of 15 (15, 30, 45…) to determine that there are 180 chairs in total.
Some students may choose to decompose 15 (10 and 5) and 12 (10 and 2) in order to make a connection to base ten materials (rods and small cubes). The corresponding open array is more abstract since it represents groupings of chairs rather than each chair.

The open array is easier to draw and is used to determine the total number of chairs from a sum of partial products (for example, 10 rows of 10 chairs give 100 chairs, 10 rows of 5 chairs give 50 chairs…). In total, there are \(100\; + \;50\; + \;20\; + \;10\; = \;180\) chairs. The open array can also be seen as a representation of a flat (the 100 chairs), 5 rods (the 50 chairs), 2 rods (the 20 chairs) and 10 small cubes (the 10 chairs). Students can also relate this to the concept of area (for example, 4 rectangles with areas of 100 chairs, 50 chairs, 20 chairs, and 10 chairs).
Source: translated from Guide d'enseignement efficace des mathématiques de la maternelle à la 6e année, Fascicule 5, p. 61-62.
Calculations can be done using arrays on grid paper. For example, to calculate \(16; \times \;34\):

To better calculate the number of squares, thick lines are drawn to delineate the groupings of 10 of each factor.
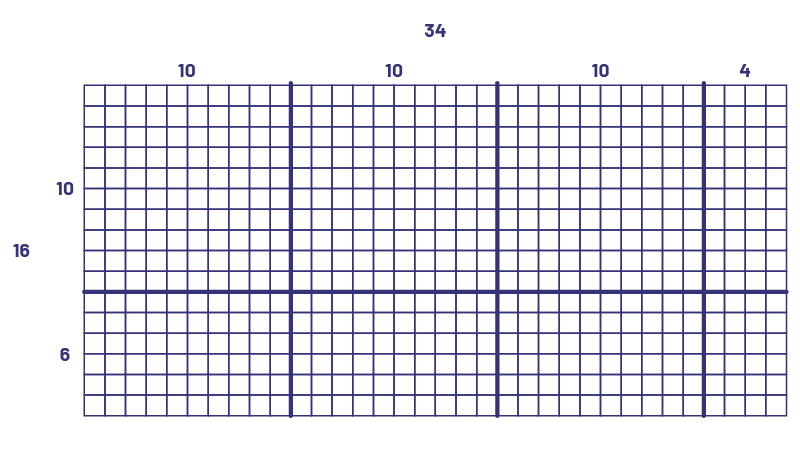
This way, you can see the 3 hundreds. To better see the tens and ones, you can also thicken some lines.
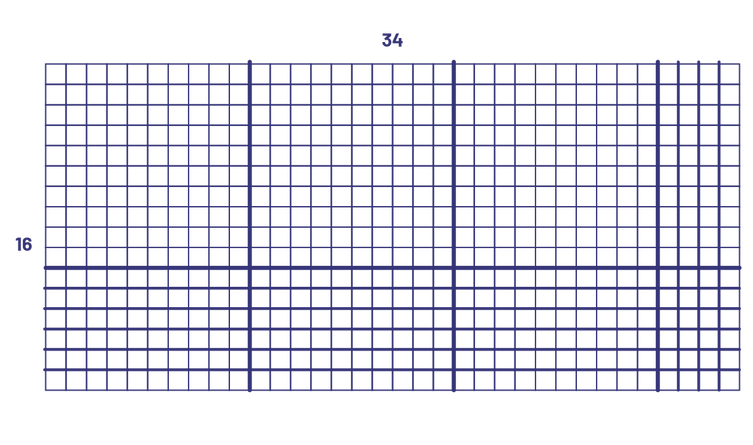
Now there are 18 tens: 4 "rods" in the upper right and then 6 "rods" + 6 "rods" + 6 "rods" in the bottom rows making a total of 22 tens. Finally, 24 ones can be seen at the bottom right. The 20 tens can be regrouped to make 2 hundreds and 20 ones can be regrouped to make 2 tens. This will result in 5 hundreds, 4 tens and 4 ones, or 544. This representation is similar to an array created with base ten blocks.
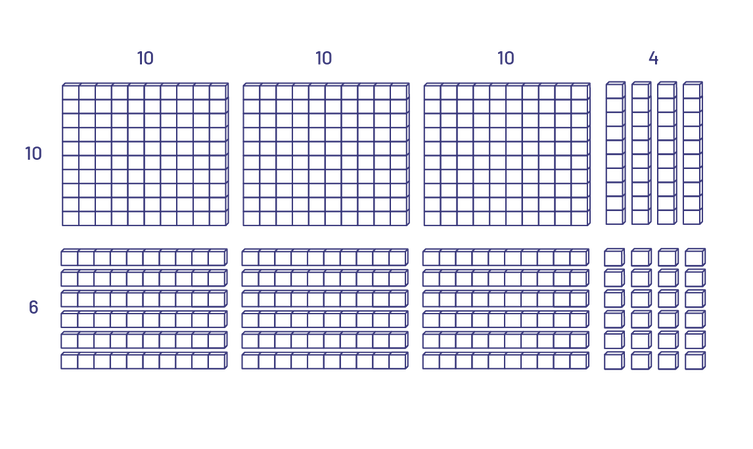
In the previous examples, every row and columns is shown. Therefore, the ones are identifiable. Over time, students can represent the same situation differently by creating various arrays where each one is not represented (open arrays). The following are other open arrays that represent \(16\; \times \;34\).
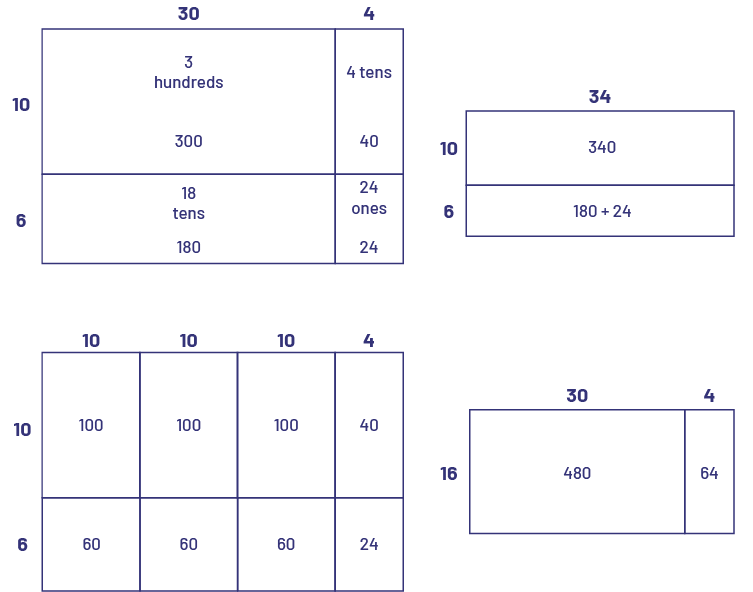
Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 1, Nombres naturels, p. 135-136.
Link Between the Area Model and the Algorithms
As students develop the ability to use open arrays and the area model and begin to understand the strategy of adding partial products related to these models, they are able to solve multiplication problems on larger numbers by breaking down each of the two factors into tens and ones. The area model is useful for representing decomposition and partial products as illustrated in the following example:
There are 35 rides at the fair. Each ride accommodates 27 people. How many people can be accommodated on all the rides?
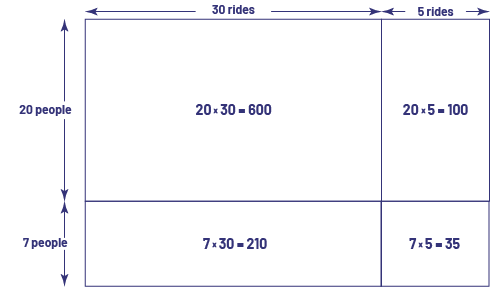
When the number 35 is decomposed into 30 and 5, and the number 27 is decomposed into 20 and 7, the product of \(35\; \times \;27\) becomes the sum of four easy-to-calculate partial products, that is \(\left( {20\; \times \;30} \right)\; + \;\left( {20\; \times \;5} \right)\; + \;\left ( {7\; \times \;30} \right)\; + \;\left( {7\; \times \;5} \right)\), for a total of 945 people.
At this time, teachers may suggest that students record these partial products in a place value chart as below:
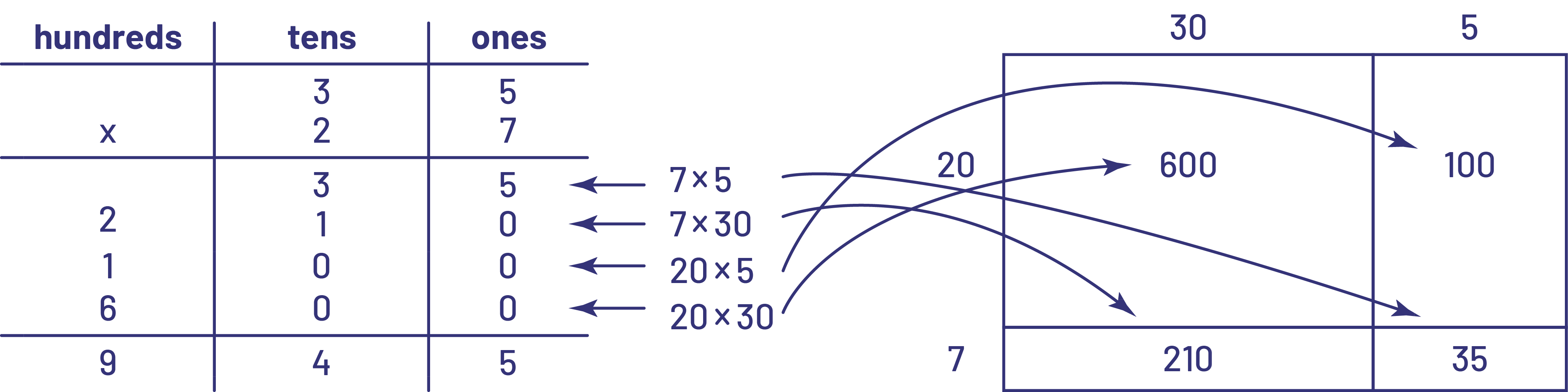
The order in which students record their partial products in the table is not important. Once students have mastered the use of a place value chart to record the partial products associated with any multiplication, teachers can introduce the standard multiplication algorithm. It is important to emphasize the connection between the steps in the algorithm and the steps in the place value table. Students will then understand that the standard algorithm for multiplication is just a quick way to reduce multiplication to a sum of partial products.

By learning and practicing multiple ways to represent operations, students develop a better conceptual understanding of multiplication and are more successful in determining the product.
Source: translated from Guide d'enseignement efficace des mathématiques de la maternelle à la 6e année, Fascicule 5, p. 63-64.
