B2.4 Represent and solve problems involving the addition and subtraction of whole numbers and decimal numbers, using estimation and algorithms.
Skill: Representing and Solving Addition and Subtraction Problems Using Strategies Including Algorithms
Learning mathematical operations takes place gradually. The starting point should be the exploration of operations in problem-solving situations. Students learn to associate situations with particular operations, which allows them to begin to make sense of the operations. Students need to use strategies based on their understanding of the context, the problem, and the operations. Students become aware that there are many ways to solve a problem and even many ways to carry out the same operation. As such, students should be asked to solve a variety of problems in order to progress towards using more effective strategies.
Contrary to the traditional practice of having students mainly learn to apply standard algorithms, learning operations should be more oriented towards understanding the operations, exploring mental strategies, and using various strategies to carry out operations. Students in the junior grades must be able to solve problems related to the operations studied using various strategies or personal algorithms.
In order to meet this expectation, students must be put in a problem-solving situation. This will allow them to develop and explore various strategies or personal algorithms.
To support students in developing effective strategies, it is important to offer them various types of problems in such a way as to allow them to grasp the multiple meanings of operations. A well-chosen problem and the application of a thoughtful strategy are more profitable than a series of mechanically completed exercises. It is therefore necessary to allocate the necessary time that will allow the students to understand and consolidate different strategies and approaches.
The exploration of strategies (including flexible algorithms) is essential to developing a robust number and operation sense. These strategies and flexible algorithms are the way for students to "play" with numbers and operations. Furthermore, these strategies that are put on paper also have the potential to translate into mental math strategies. For example, students who use a number chart or number line to perform a calculation such as \(36\; + \;52\) may later follow a similar reasoning mentally.
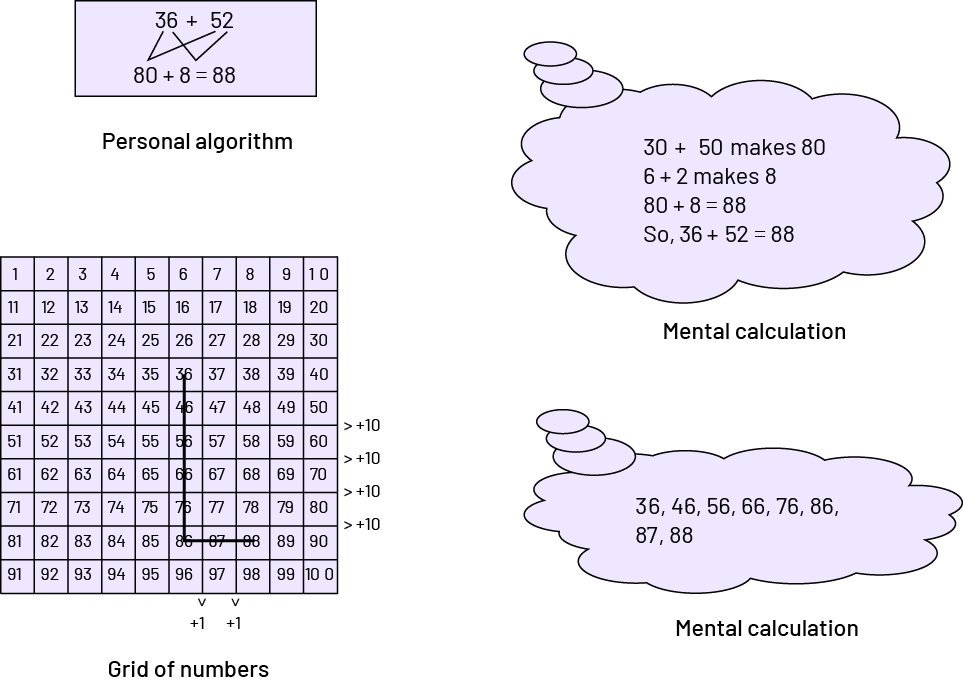
In addition, it is essential to animate mathematical conversations or discussions relating to the use of these strategies and to personal algorithms. These conversations promote the sharing of strategies and the recognition of the connections between them. Each student's personal strategies are clarified, refined and become more effective as they make connections between their and other strategies. Thus, "teachers guide the discussion by using strategies that students have used to initiate understanding of specific mathematical concepts and to direct students' progress towards effective methods" (Ministry of Education of the Ontario, 2004a, page 18).
The teacher's role is to support students in representing their thinking both visually using (semi-concrete) representations and symbolically, and to help them to see and make connections between the two. For example, a teacher might make the link between one student’s work with a concrete model and another student’s work that shows the same thinking using a symbolic representation.

Similarly, when the student physically takes 10 groups of 10 ones and realizes that it is a group of 100 ones called a hundred, a teacher might help the student notice that this concept of grouping is the same grouping which is symbolized by the writing of the number “1” above the hundreds position in the standard algorithm.

Scaffolding by teachers helps students to understand the underlying concepts associated with various operations (for example, exchanging units in subtraction). Mathematical conversations are an opportunity to present new strategies, make connections between strategies, and point or draw out efficiencies. Teachers and students could model strategies by making sure to verbalize the reasoning behind them. Later, the standard algorithm can be presented, ensuring that the students understand the underlying concepts and the reasons for the actions taken. Common algorithms should be seen by students as just another way of performing operations.
Throughout the Junior Division, it is important to present a variety of problem-solving situations, even if students have mastered several strategies for performing the various operations. This allows them to build a network of representations, skills and connections and to develop flexibility in the use of operations. Students reflect on the types of calculations to be performed (for example, estimation, exact calculation), the operations to be performed, and the effective strategies to be used depending on the situation (for example, mental calculation, usual algorithm, personal strategy).
Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 1, Nombres naturels, p. 75-78.
Written Problems: Addition and Subtraction
In addition and subtraction, quantities are changed (joined or separated), combined or compared. In order for students to understand the connections between quantities in each of these cases, it is important that they be presented with a variety of problem types.
Addition and subtraction are operations that can be used to solve problems. Therefore, it is important to avoid referring to them as "subtraction problems" or "addition problems" because it is the understanding of the situation, as well as the understanding of the operations, that leads to the choice of using addition or subtraction to solve it. Thus, students must analyze the problem, choose a strategy and apply it, just as adults do. In this context, the teacher's role is to assist students in their analysis and understanding of operations.
It is important to note that the problems presented below appear similar due to their context. However, for students, each situation represents a unique problem. It is by having experience with these various types of problems that students become proficient with addition and subtraction and knowing when to each.
Join Problems
The part-whole model can be useful for representing known and unknown values in joining problems.
The set model is useful for representing the joining of a quantity to another.
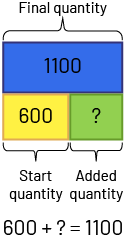
- Change situation: Result (Final quantity) unknown - Jamil has a bag of 600 candies. He buys 500 more pieces of candy. How much candy does Jamil have now?

- Change situation: Start (Initial quantity) unknown - Jamil has many candies. He buys 500 more. He now has 1100. How many pieces of candy did Jamil have to start?

- Change situation: Change (Added quantity) unknown - Jamil has a bag of 600 candies. He buys many more. He now has 1100 pieces. How much candy did Jamil buy?
Separate Problems
The part-whole model can be useful for representing known and unknown values in separating problems. The set model is useful for representing the removal of a quantity.
- Separating: Result (Final quantity) unknown. Nadia has $1500. She gives $500 to her brother. How many dollars does she have left now?

- Separating: Change (Withdrawn quantity) unknown - Nadia has $1500. She gives some to her brother. She now has $1000 left. How much money did Nadia give to her brother?

- Separating: Start (Initial quantity) unknown - Nadia had a certain amount of money. She gave $500 to her brother. She now has $1000 left. How much money did Nadia have at the beginning?

Combine (Part-Part-Whole) Problems
The part-whole model can be useful for representing known and unknown parts of the whole or the known and unknown whole in meeting problems.
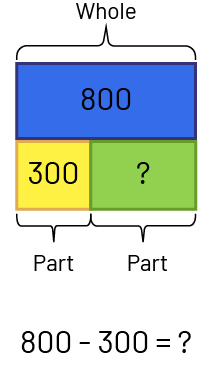
- Combining: Part unknown - The class has 800 coloured pencils, and 300 of those pencils are red. The remaining crayons are blue. How many blue crayons does the class have?
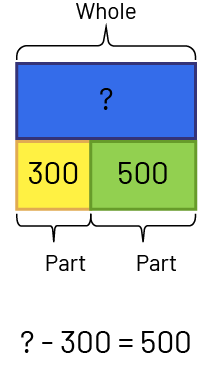
- Combining: Whole unknown - The class has a lot of coloured pencils. There are 300 red crayons and 500 blue crayons. How many crayons does the class have?
Compare Problems
The linear model can be useful for representing the difference between two numbers in comparison problems. In this example, we use relational rods and a double number line.
- Comparing: Difference unknown. Judith has $600 and Jeanne has $300. How many more dollars does Judith have than Jeanne? OR Judith has $600 and Jeanne has $300. How much less does Jeanne have than Judith?
I know that the dark green rod represents 6 (hundreds), so I placed it at the top of the number line starting at 0. I know that the lime green rod represents 3 (hundreds), so I placed it below the number line starting at 0. I compared the two rods and saw that the lime green rod is 3 (hundreds) less than the dark green rod. I found the difference or gap between the two quantities. There is a difference of $300. Judith has $300 more than Jeanne or Jeanne has $300 less than Judith.
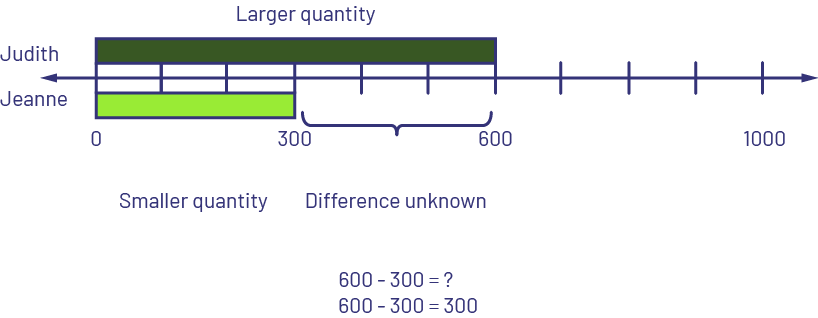
- Comparing: Larger quantity unknown - Judith has $300 more than Jeanne. Jeanne has $300. How many dollars does Judith have? OR Jeanne has $300 less than Judith. Jeanne has $300. How many dollars does Judith have?
I know that the lime green rod represents 3 (hundreds), so I placed it on top of the number line starting at 0. I took another lime green rod and placed it below the number line starting at 0 and added another lime green rod since Judith has $300 more than Jeanne. I replaced the two lime green rods with the dark green rod that represents 6 (hundreds). Judith therefore has $600.
\(?\; - \;300\; = \;300\)
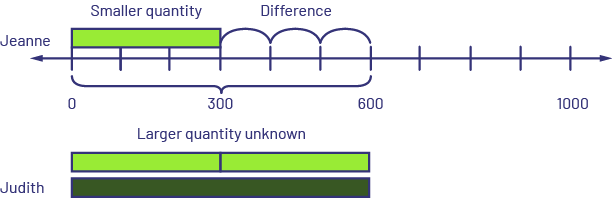
- Comparing: Smaller quantity unknown - Judith has $600 and Jeanne has $300 less than Judith. How many dollars does Jeanne have? Or Jeanne has $300 less than Judith. Judith has $600. How many dollars does Jeanne have?
I know that the dark green rod represents 6 (hundreds), so I placed it at the top of the number line starting at 0. On the number line, I counted backwards three jumps to 300 to represent that Jeanne has $300 less than Judith. I took a lime green rod, which represents 3 (hundreds), and placed it under the number line starting at 0. Jeanne has $300.
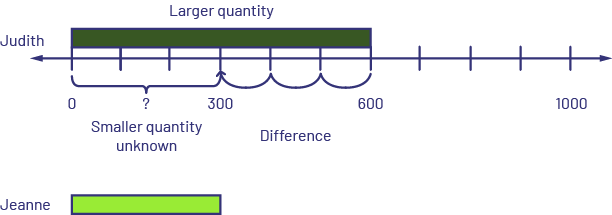
\(600\; - \;?\; = \;300\)
Source: Adapted and translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Fascicule 5, p 7-10.
Adding and subtracting problems are seen by students as active situations, easier to model and “see” as the initial quantity increases or decreases. Combining problems, however, assume a static situation because no action or change occurs, which makes them more abstract and harder to understand. Comparing problems, on the other hand, deal with the relationship between two quantities by finding the difference between them: there is therefore no action, but a comparison of one quantity with another.
Since students are regularly exposed to problems whose final quantity is sought, they solve these kinds of problems more easily. They have more difficulty solving problems in which the unknown is the starting quantity, the added quantity or the removed quantity. These variations of problems help develop a more solid understanding of addition and subtraction and the relationships between them. For example, in addition problems where the unknown value is the start quantity, students more easily see the advantages of addition (for example, \(?\; + \;12\; = \;37 \)) which makes it possible to respect the order in which the action takes place in the problem. This allows them to use a strategy (for example, counting on or counting down) to determine the start quantity. These students demonstrate their understanding of the problem and their ability to use a strategy to solve it. However, they do not demonstrate an understanding of the meaning of difference (and subtraction). If they had used the subtraction \(37\; - \;12\; = \;?\), they would have demonstrated a broader understanding of the relationships between the quantities. Having said that, when students are learning, there is no need to impose a strategy.
Requiring students to subtract will not help students who do not see the relevance of this strategy. However, if they are regularly exposed to a variety of problems and participate in the mathematical discussions that follow, they will begin to see the connections between various strategies and to learn a variety of strategies. They then become more successful.
Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 1, Nombres naturels, p. 83-84.
Relationships Between Operations
The fundamental operations of addition, subtraction, multiplication and division are closely related despite their apparent differences. The more opportunities students have to work with the operations, the more they can notice and understand the connections between them.
Addition and subtraction are inverse operations. However, when they are learning, students often have difficulty solving equations such as \(17 + \Delta = 31\). Many teachers encourage their students to use the inverse operation, namely subtraction. However, it may be learning a trick, unless students understand why subtraction is a possible strategy. They must first grasp the relationship of the whole and its parts as well as the meaning of a difference. For example, a number can be represented as follows:
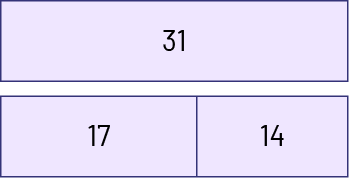
This way of representing the relationship between a number and its parts allows us to see that subtraction is the inverse operation of addition. Thus, since \(17 + 14\; = 31\) and \(14 + 17\; = 31\), then \(31 - 17\; = 14\) and \(31 - 14\; = 17\).
Additionally, students can see why addition is commutative (\(14 + 17\; = 17 + 14\)) and why subtraction is not (\(31 - 17 \ne 17 - 31\) ). Those who have acquired good number sense and are able to break down and regroup numbers can use their knowledge to more effectively solve equations such as \(17 + \;? = 31\) understanding that we are looking for the difference between 17 and 31.
Compensation Strategy
In addition to inverse operations, students can use the compensation strategy that follows from the equality relationship. This strategy involves changing the terms of an operation without changing the result and involves the conservation of the equality of quantities involved.
With this strategy, the addends for an addition expression are changed. For example, to calculate 143 + 218, the number 143 could be changed to 140 in order to facilitate the calculation. To do this, we subtract 3 from 143 and then add 3 to 218. The total number has not changed. The numerical expression becomes 140 + 221. In concrete terms, if we consider that we have 143 objects in a pile and 218 objects in a second pile, we move 3 objects from the first pile to the second pile. The total number has not changed. Therefore, \(143\; + \;218\; = \;140\; + \;221\), for a sum of 361.
Compensation is used to make an expression easier to evaluate. It can be involved adding a quantity to make a number that is easier to work with, such as a multiple of 10 or 25, and later subtracting to compensate. In the following example, we add 10 to the number 390 to make 400, which is easy to add. Then 10 is subtracted from the answer.
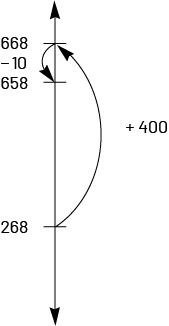
\(\begin{array}{l}268\; + \;390\; = \;?\\268\; + \;400\; = \;668\\668\; - \;10\; = \;658\\\end{array}\)
Therefore, 268 + 390 = 658
We can visualize the situation using a vertical numerical line. We can see that in this case, a number greater than that of the expression (\( + \;400\)) has been added. The desired result has thus been exceeded. We must therefore subtract the excess (\( - \;10\)).
Compensation also applies to subtraction. Since we are looking for the difference between the two terms, we modify the two terms so as to keep the same difference between them. To do this, one can add the same quantity to both terms or subtract the same quantity from both terms. For example, to calculate \(72\; - \;37\), one can add 3 to 72 to get a more familiar number, 75, while adding 3 to 37 to maintain the same difference.
\(\begin{align}72\; - \;37\; &= \;\left( {72\; + \;3} \right)\; - \;\left( {37\; + \; 3} \right)\\ &= \;75\; - \;40\\ &= \;35\end{align}\)

For this same expression, we could also compensate by subtracting 2 from each term.
\(\begin{align}72\; - \;37\; &= \;\left( {72\; - \;2} \right)\; - \;\left( {37\; - \;2} \right)\ &= \;70\; - \;35\ &= \;35\end{align}\)
We can also use compensation to subtract a larger, but friendlier number, in the mathematical expression and then compensate by adding the overage back to the difference. In the following example, 53 (3 more than needed) is subtracted from 173 to make the subtraction easier. The extra 3 that were subtracted are then added back.
\(\begin{array}{l}173\; - \;50\; = \;?\\173\; - \;53\; = \;120\\120\; + \;3\; = \;123 \end{array}\)
Therefore, \(173 - 50 = 123\)

Compensation in subtraction uses a constant difference, such that the difference between the two numbers is preserved whether a quantity is added or removed (for example, the difference between 645 and 185 is the same as that between 650 and 190 or that between 640 and 180).
A constant difference can also be used to perform operations such as subtraction with zeros (for example, \(1000 - \;354 = \;999 - \;353)\):

Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 1, Nombres naturels, p 97-101.
Computational Strategies
Personal or invented strategies offer several advantages over the traditional teaching of usual algorithms, starting with the pride and self-confidence they foster. Students who use personal algorithms make fewer mistakes because they understand what they are doing. They also improve their knowledge and understanding of the base ten number system, on which most calculation strategies are based.
Furthermore, Van de Walle and Lovin (2006) point out that research shows that students who have been able to develop personal strategies perform as well as or better than others on standardized tests.
There are size disparities between personal algorithms and usual algorithms. Personal algorithms are usually oriented in the direction of the digits, and maintain the size of the number (for example, in the addition \(323 + \;20\), one might add 2 tens to 323, which is 343). In contrast, the standard algorithms move from left to right, position to position, without attention to the size of the quantities involved (for example, in the addition \(323 + \;20\), we do: 3 ones + 0 ones are 3 ones; 2 tens + 2 tens are 4 tens…). Since a personal algorithm is the fruit of each student's imagination and understanding, it remains highly flexible, so that it can be used in a variety of situations.
In the classroom, it is suggested that several algorithms for a single operation be examined. It is essential that students understand the reasoning behind the actions in these algorithms. Over time, this allows them to choose an effective strategy depending on the context. Teachers with culturally diverse students in their classrooms can invite them to discuss at home the method their parents use to perform addition, subtraction, multiplication or division. These students can present these methods to the class, which can provide new strategies.
The standard algorithms are often presented as the main strategy for calculation. Although they are effective, they are not always appropriate. When instruction focuses on the standard algorithm, students tend to pull out a pencil and paper to solve \(300 - 15\) and often make errors related to the complex regrouping. However, it is actually more efficient to calculate this mentally as follows: \(300\; - \;10\; = \;290\), \(290\; - \;5\; = \;285\), or even think about it as getting back change. Furthermore, the standard algorithm is not the best method to use where estimation is sufficient. Therefore, it is suggested that the standard algorithm be considered as only one of many computational strategies.
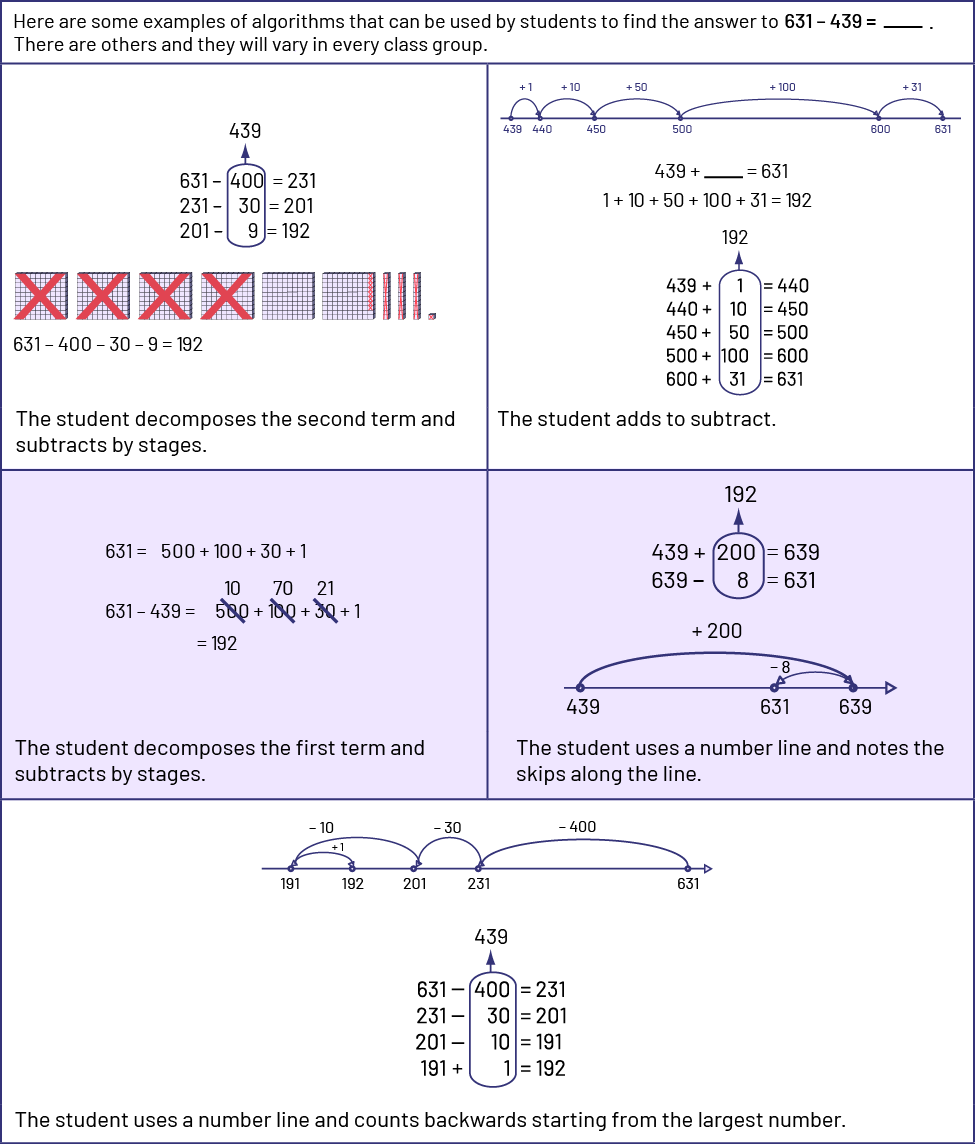
Students can solve written problems in a variety of ways. The following tables provide some examples of addition and subtraction algorithms. These are not the only ways to solve a problem, there are many others, so students should be given opportunities to reason about other ways of doing things.
Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 1, Nombres naturels, p 118-119.

Strategies to Facilitate the Understanding of Standard Algorithms
It is important to provide students with several activities to explore standard algorithms using manipulatives such as the place-value mat, interlocking cubes, ten frames, base ten blocks, number line, etc.
Teachers should provide students with many opportunities to create their own algorithms, and explain their strategies and reasoning. It is important to give students the opportunity and time to explore algorithms in great depth and engage in discussions about them. It is important to encourage students to work in pairs (one student writes down the steps while the other works with the concrete representation). Understanding the meaning of the steps in a standard algorithm develops when teachers allow students to compare it to their own algorithm in order to make connections between the two approaches, such as "add from left to right and combine".
Source: translated from Guide d'enseignement efficace de la maternelle à la 6e année, Fascicule 5, p. 56.
Adding Multi-Digit Numbers Without Grouping
Adding large numbers can be represented on a number line. For example, students could perform \(435\; + \;223\) by decomposing \(223\;\left( {200\; + \;15\; + \;8} \right)\) and adding it on to 435 as follows:
Student-Generated Algorithm
\(\begin{array}{l}435\; + \;200\; = \;635\\635\; + \;15\; = \;650\\650\; + \;8\; = \;658\end{array}\)
Usual Algorithm
\begin{array}{r}
\;\;\,435 \\
\underline{+223} \\
\;\;\,658
\end{array}
Over time, students gradually develop their sense of abstraction and can use the same strategy without using a number line but by performing the calculation mentally.
Adding Multi-Digit Numbers with Grouping
It is important for students to practice grouping 10 ones into tens, 10 tens into hundreds, and so on. They will need the support of visual representations of groupings to develop a conceptual understanding of the algorithm.
The base ten blocks help some students visualize the operation more clearly by allowing them to regroup by exchanging ten rods for a flat, for example:

Students can also use a place value mat that organizes the material by the position of the digit in the number.

The same numeric expression (\(186\; + \;156\)) can be represented using drawings. In this way, students demonstrate some level of abstraction since a drawing is used to represent 100, 10 or 1.
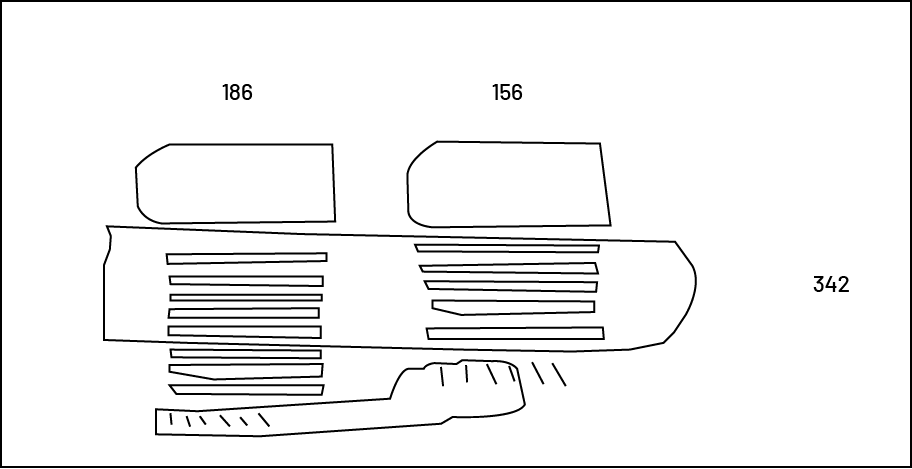
Source: Adapted and translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 1, Nombres naturels, p 122-124.
Subtraction Without Regrouping
As with addition, students often use manipulatives to perform subtraction. This strategy helps them grasp the concept of separating, although it is not very effective when dealing with large numbers.

Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 1, Nombres naturels,, p. 127.
The base ten blocks allow students to perform subtraction by separating, or removing a quantity. For example:
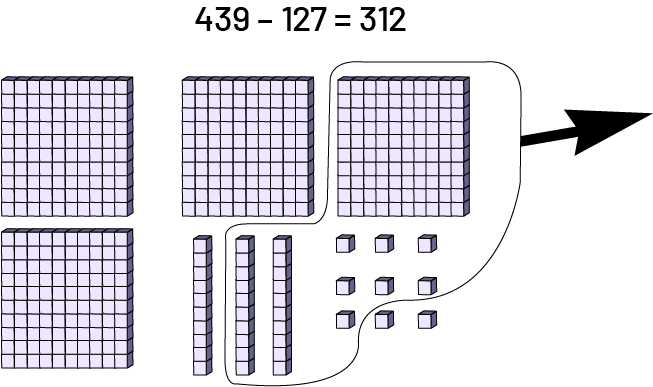
If they use the place value mat for subtraction, some students tend to represent both terms. The subtraction is then performed by comparison. For example:

Source: Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 1, Nombres naturels, p. 128.
Subtraction With Regrouping
Exploring subtraction with regrouping promotes conceptual understanding. Teachers should encourage students to use the place-value mat and base ten blocks to model subtraction with regrouping. Students can work in pairs. They can move on to the written form of the algorithm once they have developed a solid understanding of it through modeling.
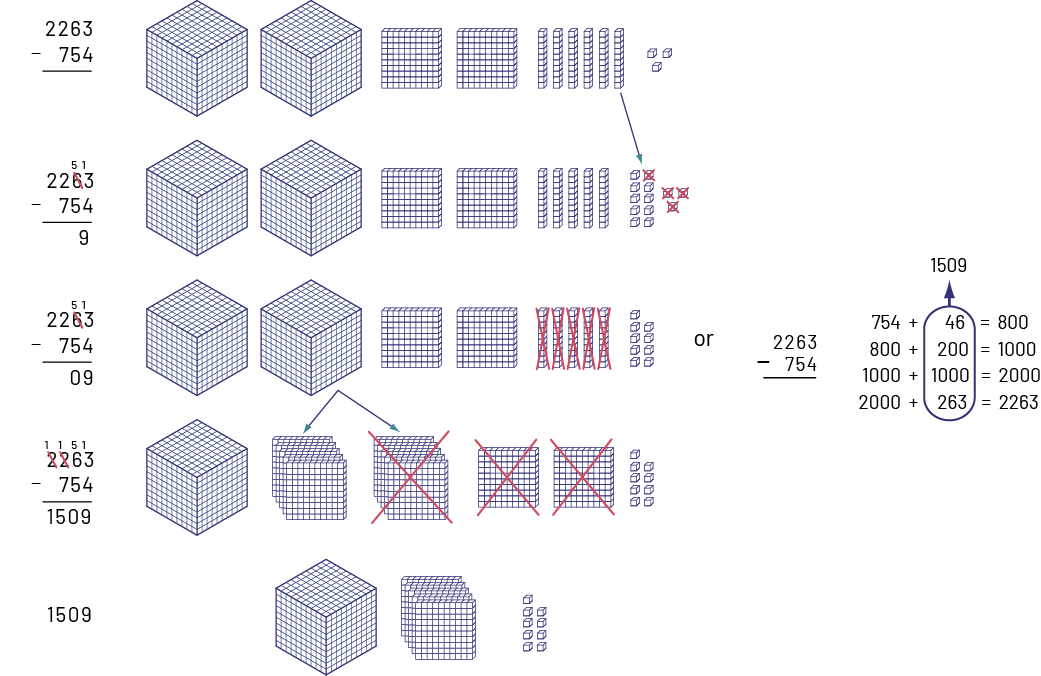
In the \(325\; - \;118\) problem, students model the first number (325) with base ten blocks on the top portion of the place value mat. Unable to withdraw 8 units since there are only 5, the students will have to exchange a ten for 10 ones.
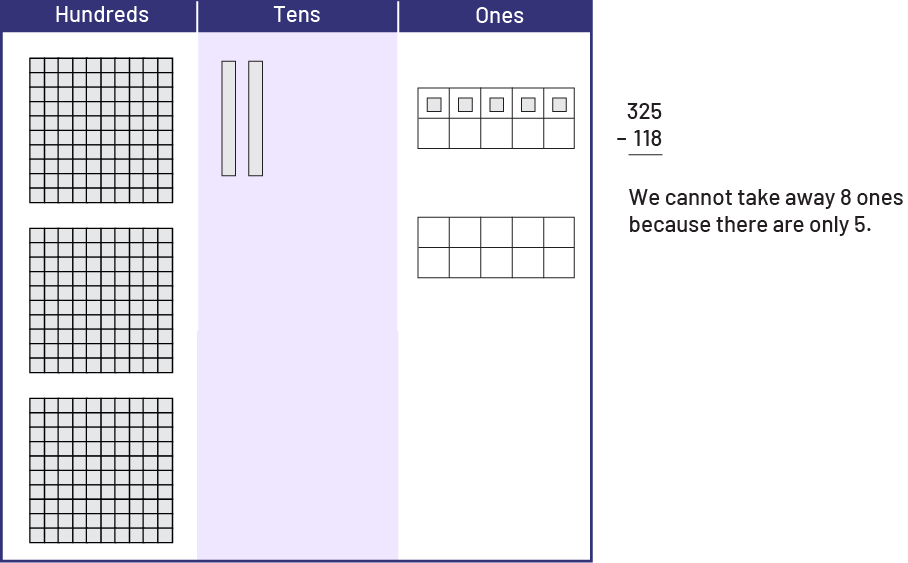

This gives them a group of 15 ones from which they can now remove 8 so that 7 ones remain. Students should be encouraged to group the ones on the mat to better organize their work.
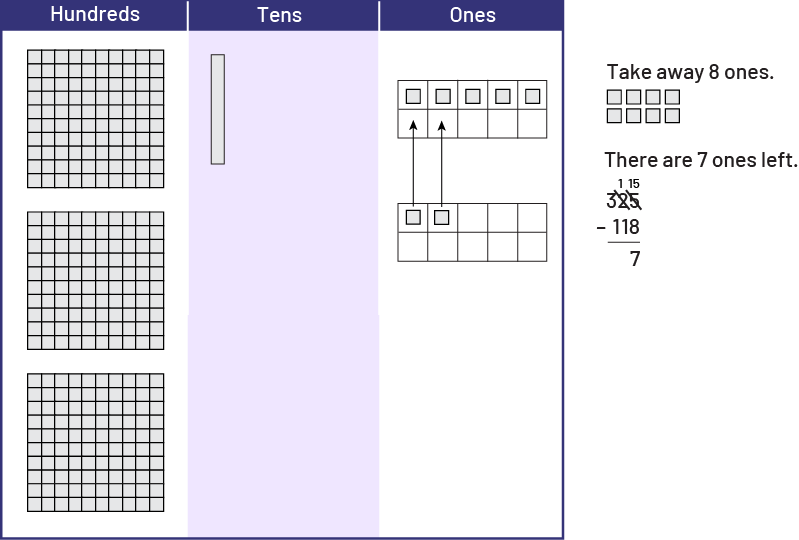
Students now remove 1 ten and 1 hundred and place them outside the mat.
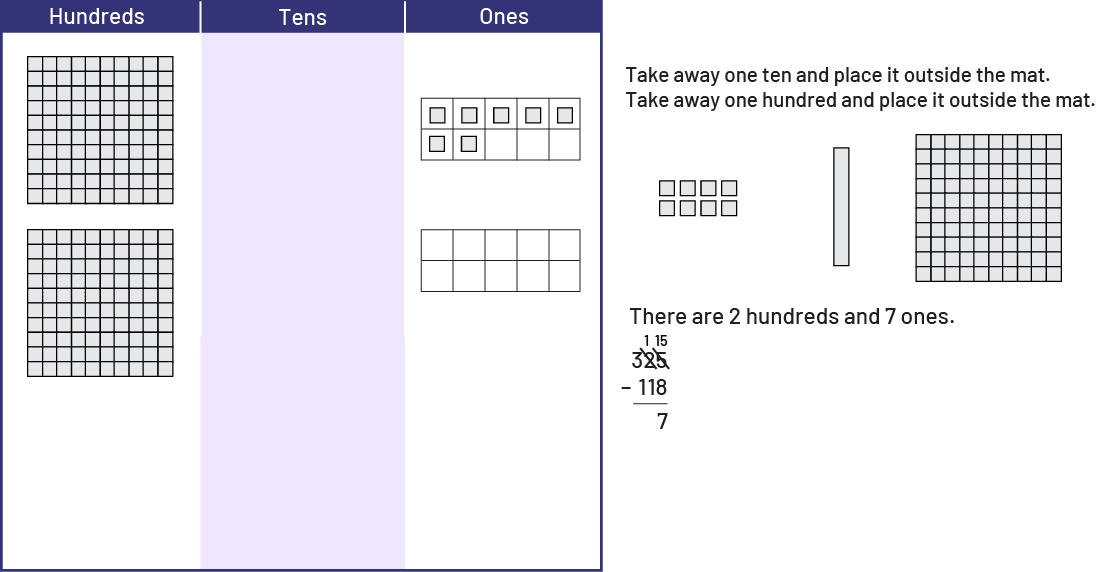
So, \(325\; - \;118\; = \;207\).
Source: translated from Guide d’enseignement efficace des mathématiques de la maternelle à la 6e année, Fascicule 5, p 58-59.
Students can also use the number line to perform a subtraction. For example, to calculate \(263\; - \;45\), they can use compensation to work with "friendlier" numbers. Since \(263 + 2 = 265\), it is easier to determine \(265 - 45 = 220\) and then subtract 2 to compensate (\(263\; + \;2\; - \;45\; - \;2\)).
Students can show their thinking on the number line by labelling the jumps:
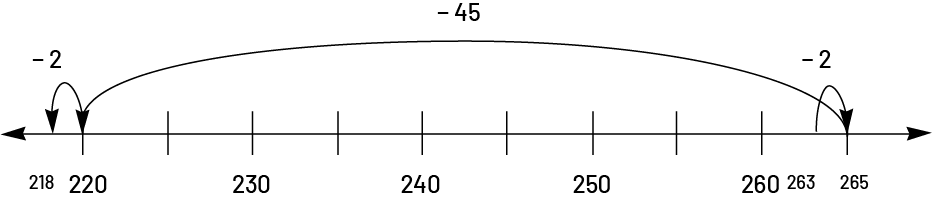
The number line can also be used with the decomposition by removing in jumps according to the place values of the subtrahend, or number being removed (\(263 - 40 = 223\), \(223 - 5 = 218\)):
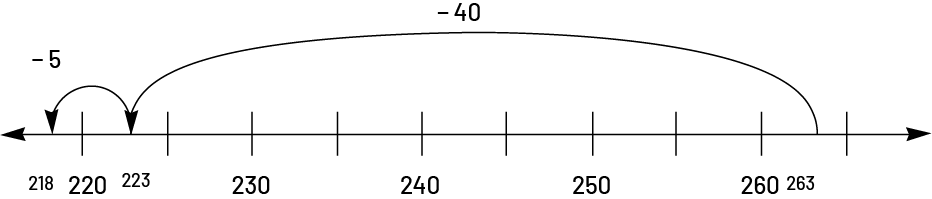
The open number line allows students to proceed in significant leaps \((263\; - \;3\; = \;260,\;260\; - \;40\; = \;220,\;220\; - \;2\; = \;218)\):

Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 1, Nombres naturels, p. 127.
Students can use drawings to quickly illustrate a number expression such as \(1369 - 821\). Numbers can be represented by lines, circles, dots, etc. A separation or removal can be expressed by hatch marks on the drawing. For \(1369 - 821\), we must subtract 8 hundreds, 2 tens and 1 one from the 13 hundreds, 6 tens and 9 ones.
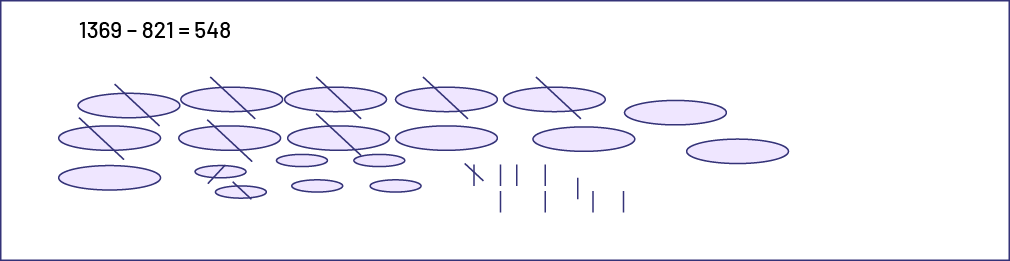
Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 1, Nombres naturels, p. 129.
Link Between a Personal Algorithm and a Standard Algorithm
Giving students the opportunity to model addition and subtraction with regrouping on multi-digit numbers allows them to visualize the steps of the corresponding standard algorithm. The steps of an algorithm are not out of context when conceptual understanding is present. Students who have forgotten a step in the usual algorithm can still find a solution to the problem since they have the ability to use a personal algorithm.
With practice modeling, students can move on to writing down the standard algorithm using blank tables to keep track of the steps modeled on the place value mat.
Addition

| Sample Questions | Examples of Answers | |
|---|---|---|
|
Empty Cell |
Low Level of Understanding | Good Level of Understanding |
| When you add up the ones, what do you say? |
Empty Cell |
\(0\; + \;5\; = \;5\) |
| When you add up the tens, what do you say? | \(0\; + \;3\; = \;3\) | \(0\; + \;30\; = \;30\) |
| When you add up the hundreds, what do you say? | \(7\; + \;5\; = \;12\) | \(700\; + \;500\; = \;1200\) |
| What do you write in the hundreds column? | 2 | 2 hundreds |
| What do you remember? | 1 | 1 thousand |
| When you say that 7 hundreds and 5 hundreds make 12 hundreds, how do you know that you are regrouping the 1 and not the 2? | That's the way it is. | In 1200 there are 1 thousand and 2 hundreds. |
| What does the 1 above the thousands represent? | 1 | 1000 |
| Why do you show the regrouping there? | Because that's the next column. | Because I'm going to add all the thousands together. |
| When you add up the thousands, what do you say? | \(1\; + \;1\; + \;2\; = \;4\) | \(1000\; + \;1000\; + \;2000\; = \;4000\) |
| Do we always have to regroup? | No | Regroupings are made if you get 10 or more in a column. |
Subtraction
| Sample Questions | Examples of Answers | |
|---|---|---|
|
Empty Cell |
Low Level of Understanding | Good Level of Understanding |
| When you subtract the ones, what happens? | (3 - 4) is not possible. | There are not enough ones to subtract 4 in the ones column. |
| What do you do to calculate the units? | I borrow 1 from the other column. | I borrow ten, so I can say \(13\; - \;4\). |
| Why are you regrouping? | Because 4 can not be subtracted from 3. | I need more ones, so I am changing a ten into 10 ones, adding it to the 3 ones I already have and then I can remove 4 ones. |
| What does the 1 represent? the 5? | The 1 goes with the 3 and the 5 is 5. | The 1 is 10 and the 5 is 50. |
| What do you say when you subtract the tens? | \(5\; - \;5\; = \;0\) | \(50\; - \;50\; = \;0\) |
| What do you say when you subtract the hundreds? | It is not possible. | Because \(200\; - \;700\) is impossible, I need more hundreds in this column. |
| What do you do then? | I borrow 1 from the other column. | I take a thousand and put it with the 2 hundreds. |
| How do you show that you've regrouped? | I cross out the 2, write 1 above it and put a 1 next to the 2. | I have 2 thousands but I need to regroup one of them into hundreds. I only have 1 thousand left which you can see with this 1. I wrote a 1 in front of the 2 in the hundreds because I now have 1200. |
| What do you say when you subtract the thousands? | 1 | \(1000\; - \;0\; = \;1000\) |
Source: translated from Les mathématiques...un peu, beaucoup, à la folie!, Guide pédagogique, Numération et sens du nombre, 4e, Module 1, Série 3, p. 235-238.
Skill: Estimating the Outcome of an Operation
Estimating the result of an operation means determining the approximate value of the operation in writing or mentally. Students often have difficulty with estimation because they have difficulty recognizing that more than one answer may be acceptable for a given situation. For example, they may calculate the correct answer for an estimate and then round it off.
Estimation is extremely useful in everyday situations. It may even be the only possible or desired answer. For example, when shopping, you want to know the total cost of your purchases to be able to stick to your budget. In this case, we want an approximate idea of the result, not the exact total cost.
Estimation is often used to provide a preview of the expected result or to check the reasonableness of the solution. Students need to develop the ability to make a quick mental estimation as soon as a calculation is to be performed in order to get a general idea of the result. Unfortunately, many students do not make the connection between the estimation and the correct result; the estimation is then seen as another calculation that must be performed and not as an informally performed strategy that confirms the reasonableness of the calculation.
Teachers need to use a variety of teaching strategies to make students aware of the purpose of estimation. For example, students do not see the relevance of estimation if the exact result always accompanies the estimation. Teachers should present situations in which the solution to the problem is an estimate or problems that do not require a precise answer (for example, determining each citizen's share of the national debt or shopping for school supplies for next year).
Since on a daily basis, estimations are often the result of informal mental calculations, it is appropriate that students practice and learn to estimate in this context. Teachers should therefore ask them to estimate the result of an operation (without using paper and pencil) and to communicate this approximate result (for example, \(346 + 516\), it is close to 850).

You can also present a series of operations and ask students to perform only those that meet a certain condition (for example, perform those whose result is greater than 300). This teaching strategy can be integrated with problem solving. In the following problem, students use their estimation skills to determine which calculations need to be done with precision:
In a warehouse there are several bags of balls that contain either 1 256, 542, 368, 1856, 325, 1379 or 730 balls. In order to facilitate transport, the bags are put in boxes that can contain between 2000 and 3000 balls. On each box, you must clearly indicate the exact number of balls it contains. Determine 10 different combinations of bags that a box can contain.
 Because the result of an estimation represents an approximate rather than a precise quantity, it should not be communicated exclusively using a number (for example, instead of stating that it is 350, one can say that it is about 350). The result of an estimation can also help indicate the order of magnitude or the scale of the answer (for example, it will be at least, it will be more than, the answer must be between x and y, or the answer will be greater than).
Because the result of an estimation represents an approximate rather than a precise quantity, it should not be communicated exclusively using a number (for example, instead of stating that it is 350, one can say that it is about 350). The result of an estimation can also help indicate the order of magnitude or the scale of the answer (for example, it will be at least, it will be more than, the answer must be between x and y, or the answer will be greater than).
The ability to estimate the result of an operation is a characteristic of good operation sense. It demonstrates an ability to use numbers and operations in a variety of ways. To estimate, students use a variety of strategies such as rounding, using benchmarks, applying properties of operations, decomposing, or compensating.
The degree of accuracy in estimating the result of an operation depends on the situation and the meaning of the number. It is important to discuss acceptable estimation ranges in various contexts. For example, the estimate of the difference between 315 and 185 could be a number between 100 and 200.
Estimating the difference between 10 853 and 9445 would be a number between 1000 and 2000. Estimating the outcome of an operation requires a good understanding of the effect of operations. Rounding is often used to estimate a result and it is important to be aware of its impact on the result of the estimate. For example, rounding to the nearest hundred generally creates a larger discrepancy between the actual number and the rounded value than rounding to the nearest ten.
Example
\(353\; + \;129\)
Exact result: 482
Estimate by rounding the numbers to the nearest hundred: \(400\; + \;100\; = \;500\)
Estimate by rounding the numbers to the nearest 10: \(350\; + \;130\; = \;480\)
Rounding numbers has little influence on the result of an addition or subtraction since these operations produce little effect on the numbers. Rounding can help to refine an estimation. For example, the result of \(387\; + \;295\) is approximately 700. However, it can be said that the result is less than 700, since both numbers have been rounded up (\( 400\;+\;300\)). Similarly, \(1300 - 1170\) is approximately equal to 100. However, rounding up from 1170 to 1200 allows us to specify that the difference is more than 100.
Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 1, Nombres naturels, p 92-95.
Skill: Representing and Solving Problems Involving the Addition of Decimal Numbers to Hundredths, Using Appropriate Tools, Strategies, and Algorithms
To add decimals effectively, students need to understand the place value of the digits that make up each number and factor this into their calculations. They must also recognize that the decimal point is a marker that identifies the place value of digits. During an addition, to ensure the correspondence of the place values, one can align the decimal points. For students who have a good sense of addition and place value, decimal alignment is not a rule to memorize, but a way to account for place values.
When adding decimal numbers, the concept of grouping is used as it is for adding whole numbers. For example, just as one can add 3 hundreds to 8 hundreds to form 11 hundreds, one can add 3 tenths to 8 tenths to form 11 tenths. Since the base ten system does not allow two digits to be placed in the same position, students need to understand the concept of regrouping.
Example
\(8\;{\rm{tenths}}\; + \;3\;{\rm{tenths}}\; = \;11\;{\rm{tenths}}\)
(The tab  represents one)
represents one)


Since 10 tenths can be grouped into 1 one, we have 1 one and 1 tenth.

The quantity "11 tenths" is written 1.1.
Base ten blocks and the place value mat are a great support when learning about adding decimal numbers. With these materials, quantities of the same value are joined together explicitly - for example, hundredths are added together with hundredths. When students work with base-ten materials, they use their knowledge of place value and, as a result, extend the concept of grouping, transferring the concepts they applied to whole numbers to situations involving decimal numbers. Students then recognize that regardless of place value, whenever 10 elements are found in a position, they are replaced by 1 group of 10 that is placed in the position to its left. Using this type of material increases students' understanding and introduces them to algorithms for adding decimal numbers.
Based on their knowledge of whole number addition strategies and their understanding of decimal numbers, students can add them using base ten materials, a number line, a personal algorithm, or the standard algorithm. It is important that teachers engage students in making connections between these strategies in order to consolidate addition of decimal numbers.
Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 3, Nombres décimaux et pourcentages, p. 98-100.
It is also important that the student estimate the answer to a problem before solving it. Estimation is often used to provide a measure of the expected outcome or to check the reasonableness of the solution. Students should develop the reflex of mentally making a quick estimate as soon as a calculation is to be performed so that they can get a general idea of the outcome. Unfortunately, many students do not make the connection between the estimate and the correct result; the estimate is then seen as another calculation that must be performed and not as an informally performed strategy that confirms the likelihood of the calculation result.
Teachers should use a variety of teaching strategies to make students aware of the purpose of estimation. For example, students do not see the relevance of estimation if the exact result always accompanies the estimation. Teachers should present situations in which the solution to the problem is an estimate or problems that do not require an exact answer.
Example
Determine each citizen's share of the national debt or purchase school supplies for next year.
Since estimation in everyday life is often the result of informal mental calculation, it is only natural that students should practice and learn to estimate in this context.
Teachers should therefore ask them to estimate the result of an operation (without using paper and pencil) and communicate this approximate result
Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 1, Nombres naturels, p 92-93.
Example
In order to estimate the sum, it is possible to reason as follows: \(1.572\; + \;2.724\) is about \(2\; + \;3\) is about 5.
Students can then confirm their estimate using algorithms. Here are different strategies for adding two decimal numbers.
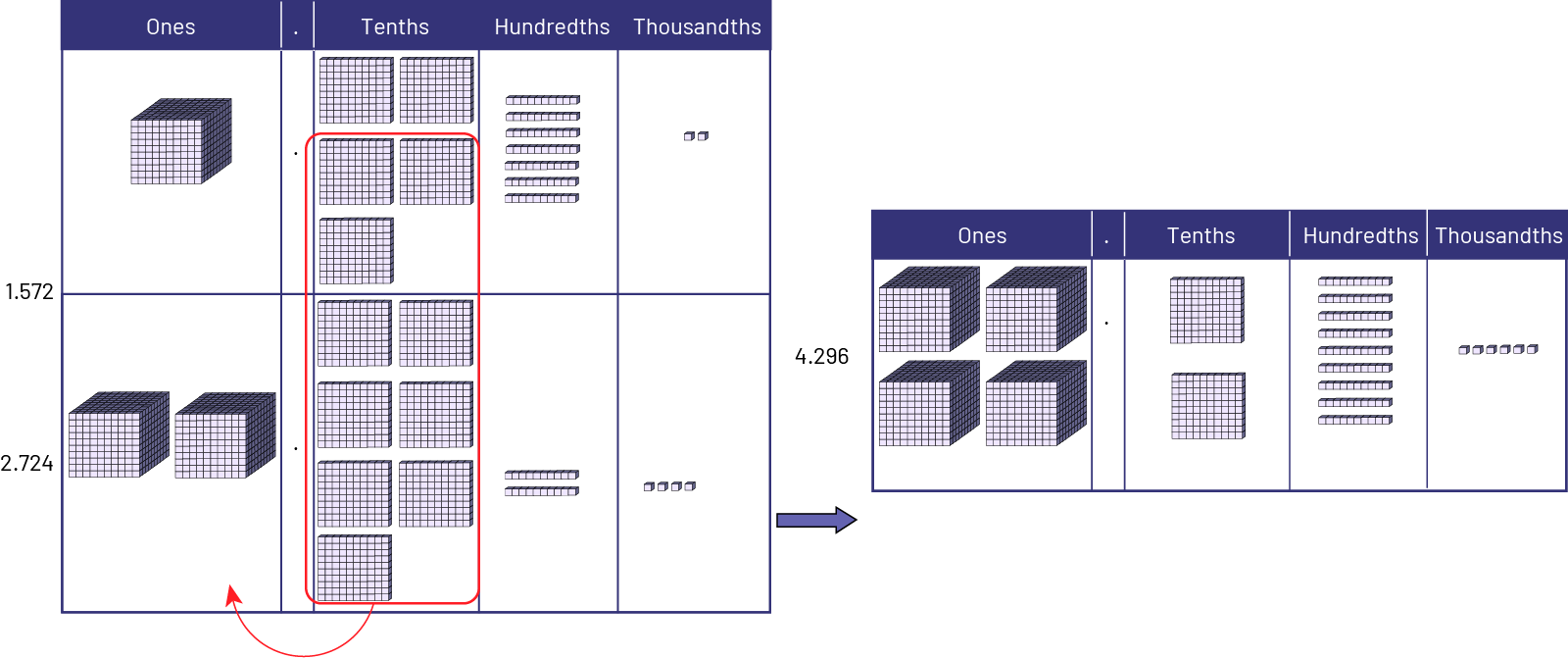
Addition Using Base Ten Blocks
To add the two quantities, each of the two numbers is represented with base ten blocks on a place value mat. By putting the blocks together, there are 3 ones, 12 tenths, 9 hundredths and 6 thousandths. Ten tenths can be exchanged for 1 one. We then have 4 ones, 2 tenths, 9 hundredths and 6 thousandths, that is 4.296.
Addition Using a Number Line
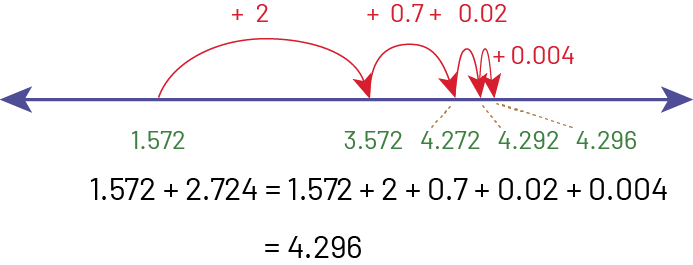
Addition Using a Student-Generated Algorithm
Numbers are decomposed according to place values.
Example

Addition Using a Standard Algorithm
Example

Source: Adapted and translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 3, Nombres décimaux et pourcentages, p 100-101.
Skill: Representing and Solving Problems Involving Subtracting Decimal Numbers up to Tenths, Using Appropriate Tools, Strategies and Algorithms
During subtraction, it is important, as it was with addition, to consider the place value of the digits that make up the numbers. The strategies for estimating the subtraction of decimal numbers and for subtracting decimal numbers are essentially the same as those used for subtracting whole numbers.
Example
\(2.724\; - \;1.572\)
In order to estimate the difference, it is possible to reason as follows: \(2.724\; - \;1.572\) is approximately \(3\; - \;2\), so approximately 1.
Students can then confirm their estimation using a variety of different strategies for subtracting two decimal numbers, such as:
Subtracting Using Base Ten Blocks
When using concrete materials to represent subtraction, students can actually manipulate quantities. To determine a difference, they can compare one quantity to another or take one quantity away from another. Students can also discover, through the use of these materials, that sometimes regrouping is necessary to make it easier to determine the difference between quantities.
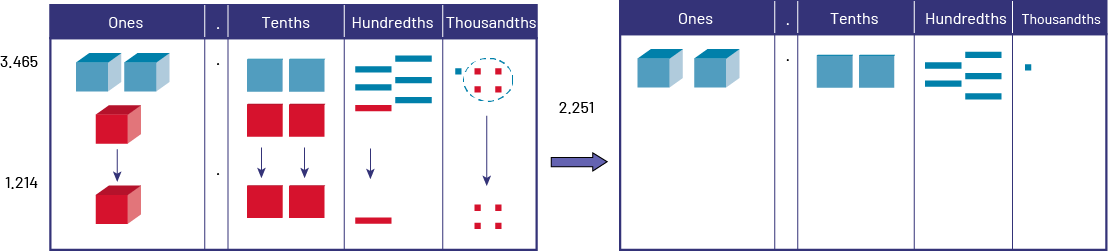
Example of Comparison
\(3.465\; - \;1.214\)
Represent each number using base ten materials and match like quantities (in red) in each position. The difference is represented by the quantities that remain in the number 3.465 (in blue). Thus, we get \(3.465\; - \;1.214\; = \;2.251\).
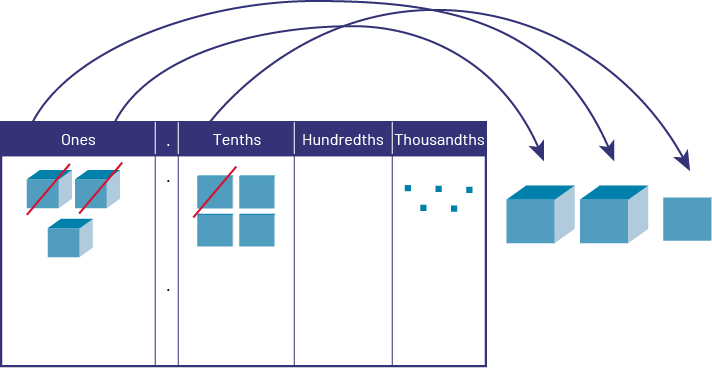
Example with Separating
\(3.405\; - \;2.1\)
The number 3.405 is represented using base ten material. Next, the equivalent of the number 2.1 is removed. The difference between the two numbers, 1.305, remains on the mat.
Example of Regrouping
\(2.423\; - \;1.26\)
The number 2.423 is represented using base ten materials. When we try to use the withdrawal strategy to perform the subtraction, we realize that there are only 2 hundredths on the mat when we should withdraw 6 hundredths. In this case, we exchange 1 tenth for 10 hundredths. We then remove the equivalent of the number 1.26.

The difference between the two numbers, 1.163, remains on the mat.
Subtracting Using a Number Line

Subtracting Using a Student-Generated Algorithm

Subtracting Using a Standard Algorithm
We can use a standard algorithm for subtraction with decimal numbers. However, you have to make sure to match the place values.

Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 1, Nombres naturels, p 101-104.
Knowledge: Algorithm
Algorithms are sets of rules and ordered actions needed to solve addition, subtraction, multiplication or division. In simple terms, an algorithm is the "recipe" for an operation. (Kilpatrick, Swafford, & Findell, 2001, p. 103)
Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 1, Nombres naturels, p. 75.
Traditionally, algorithms (standardized computational steps) were designed at a time when an elite group of "human calculators" did not have calculators (Ma, 2004). Algorithms were not designed to foster the level of understanding that we expect of students today. (Ontario Ministry of Education, 2004a, p. 13)
Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 1, Nombres naturels, p. 118.
Knowledge: Standard Algorithm
Standardized way to perform an operation, for example:
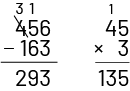
Knowledge: Student-Generated Algorithm
Strategy, generally developed by the student, to carry out an operation, for example:
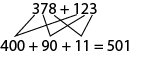
It is a strategy found intuitively by the students, allowing them to perform an operation.
Not all students invent algorithms. However, all students benefit from sharing personal strategies.
Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 1, Nombres naturels, p. 76.
Example
\(299\; + \;299\)
It is more efficient to perform this addition by thinking of \(300 + \;300 - \;2\), rather than using all the steps of the standard algorithm.
Source: translated from L’@telier - Ressources pédagogiques en ligne (atelier.on.ca).
Knowledge: Estimation
Estimation is a process by which visual and mental information is used to assess the magnitude of a quantity. Estimating the result of an operation is determining its approximate value in writing or mentally. Estimates play an important role in our daily activities by giving us approximate quantities for different situations. It may even be the only possible or desired answer.
Examples
Through the media, nearly 10 000 people were at the rally.
In our own experience, grocery shopping costs about $200 per week.
Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 1, Nombres naturels, p 36.
Estimation is an important skill associated with multi-digit number operations. This skill helps students develop their number sense and use it to understand each step of standard algorithms.
The goal of estimation is not to arrive at an exact answer, but a logical approximation. Questions such as "Is the answer less than 25?" and "Is the answer more than 10?" help students recognize possibilities and assess the reasonableness of their answers. The examples below outline some of the strategies teachers can use to support students in developing estimating skills. These strategies should not be taught as procedures to be memorized or used constantly. Instead, teachers can use them to help students better understand what they are doing and why they are doing it, when the opportunity arises. Therefore, students should not be expected to use all of these strategies, at least not until the later grades.
In Grade 6, students can use the following estimation strategies:
Clustering is useful to make numbers easier to work with.

Compatible numbers: using numbers that are easy to work with. In addition and subtraction, students look for numbers whose sum or difference is near 10.

Estimation from the left: In this type of estimation, the operation is performed using the highest place value number, with an adjustment of the remaining values.
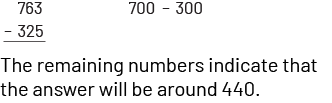
Rounding: rounding is a more complex estimation method than left-handed estimation. It requires two steps: first rounding each number and then calculating the estimate.

Many students do not understand the importance and relevance of estimation. They believe that estimating is a way of arriving at the correct answer, so they find it necessary to change their estimation after making an accurate calculation. By providing students with many opportunities to practice estimating each day, teachers can help them improve this skill and thus develop a sense of estimation and its usefulness in everyday life.
An estimation provides students with a guide to determine if their solution is likely and reasonable.
Students who have multiple experiences with estimating are more likely to understand its importance and to reason logically when working with large numbers.
Students' conceptual understanding of fundamental operations and their ability to perform mathematical operations with single- and multi-digit numbers efficiently and effectively are developed in problem-solving contexts.
Source: translated from Guide d’enseignement efficace des mathématiques de la maternelle à la 6e année, Fascicule 5, p. 68-70.
