B2.10 divide whole numbers by proper fractions, using appropriate tools and strategies
Activity 1: Division Problems
First Problem
Annick has four oranges. She gives each of her friends one orange. How many friends get a piece of orange?
(\(4 \div \frac{2}{3}\))
Second Problem
In relay races, the distance to be covered is 3 km. Each member of the team runs the full distance. How many team
members must be on the team?
(\(3\; \div \;\frac{2}{6}\))
Source: Adapted from Math: A Little, A Lot, A Lot of Fun, Teacher's Guide, Revised Edition, Numeration and Number Sense, Grade6, Unit 2, Series 2, p. 295.
Ask students questions such as:
- What strategies can be used to solve problems? What tools can be used? Justify your answer.
- How could the same situation be represented by multiplication? How do you know?
Ask students to compare their strategies with each other. Identify similarities and differences between the various strategies.
Activity 2: Visit to the Village Dairy!
Benjamin is making ice cream cones. Each size of cone requires a different amount of ice cream.
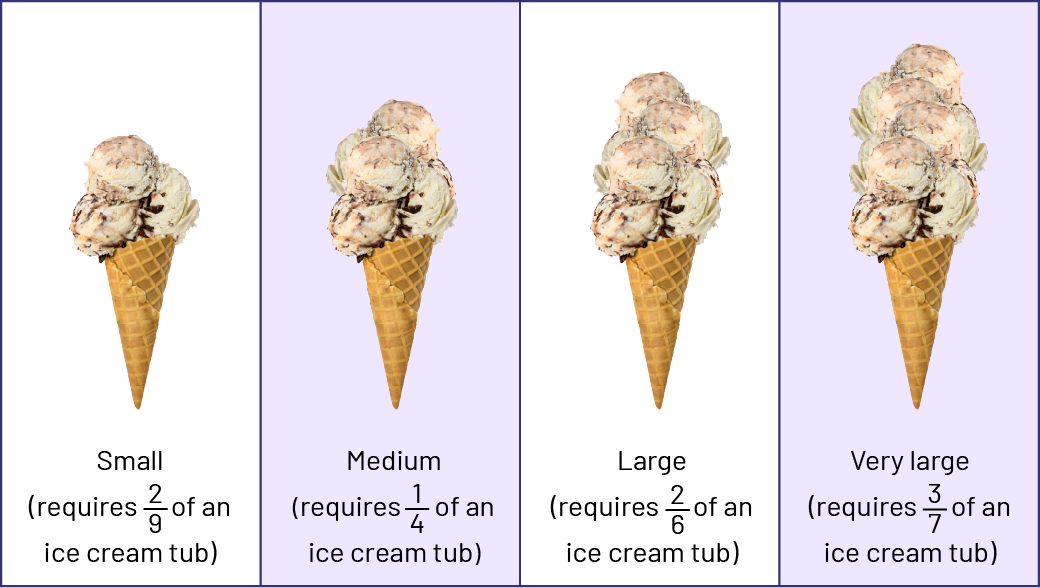
Ask students questions such as:
- How many small cones could he make if he had 6 tubs of ice cream? 2 tubs of ice cream? 8 tubs of ice cream? How do you know?
- How many average cones could he make if he had 6 tubs of ice cream? 2 tubs of ice cream? 8 tubs of ice cream? How do you know?
- How many large cones could he make if he had 6 tubs of ice cream? 2 tubs of ice cream? 8 tubs of ice cream? How do you know?
- How many really big cones could he make if he had 6 tubs of ice cream? 3 tubs of ice cream? 9 tubs of ice cream? How do you know?
- What strategies or tools could be used to solve the problems? Justify your choice.
- How could the problems be represented using multiplication? Explain your reasoning.