B1.5 Generate fractions and decimal numbers between any two quantities.
B1.5 Generate fractions and decimal numbers between any two quantities.
Equality Relationship Between a Decimal Number and a Corresponding Fraction
Students need to understand that since decimal notation is just another way of representing a decimal fraction, it is then possible to establish a relationship between the two notations (for example, \(\ 0.3 = \frac{3}{10} \)). By recognizing this equivalence, they are able to associate a place value with each of the decimal places that make up a decimal number, that is, tenths, hundredths, thousandths and so on.
Example
To establish the relationship between a fraction whose denominator is not a power of 10 (for example, \(\frac{1}{4}\)) and the corresponding decimal number, it is necessary to use the concept of equivalent fractions. For example, students can use strips of equal length as shown below to see that \(\frac{1}{4}\) is between\(\frac{2}{{10}}\) and \(\frac{3}{{10}}\).
They can then subdivide the tenths into 10 equal parts, thus creating 100 equal parts, or hundredths of the whole, and recognize that \(\frac{{25}}{{100}}\) is a fraction equivalent to \( \frac{1}{4}\).
Since \(\frac{{25}}{{100}}\), they can conclude that the fraction \(\frac{1}{4}\) can also be represented in decimal notation by 0.25 (\(\frac{1}{4}\; = \;\frac{{25}}{{100}}\; = \;0,25\)). This type of example allows students to recognize that all fractions that can be expressed as an equivalent decimal fraction can be represented by a decimal number.
Note: Some fractions (for example, \(\frac{2}{3}\), \(\frac{3}{7}\), \(\frac{5}{{11}}\)) cannot can be represented by an equivalent decimal fraction. They can, however, be expressed by decimal numbers with a repeating decimal part (for example, \(\frac{2}{3}\; = \;0,\overline{6}\); \(\frac{3 }{7}\; = \;0,\overline{428 \ 571}\); \(\frac{5}{{11}}\; = \;0,\overline{45}\)), the decimal representation being obtained by dividing the numerator by the denominator.
Source: Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 46-48.
Order Relationships
The order relationship is based on the comparison of numbers. One of the great strengths of decimal numbers is the speed with which it is possible, through the concept of place values, to compare and order quantities. For example, it is much easier to compare the numbers 0.64 and 0.75 when expressed in decimal notation rather than as the fractions \(\frac{{16}}{{25}}\) and \(\frac{{15}}{{20}}\).
In general, students have little difficulty comparing decimal numbers with the same number of decimal places (for example, 0.34; < 0.46). They have more difficulty comparing numbers with different numbers of decimal places (for example, 1.34 and 1.275). Some tend to compare these numbers without the decimal point (for example, 134; < 1 275) and conclude incorrectly that 1.34; < 1.275). Others reach the same incorrect conclusion by comparing only the numbers to the right of the decimal point (for example, \(34\; < \;275\)).
The order relationship should be addressed by comparing decimal numbers in contextualized situations. For example: "Remi did a jump of 3.55 m and Samantha did one of 3.7 m. Which of the two had the longer jump?" Students can respond and justify their choice if they understand place value. The number line is a powerful visual model for comparing decimal numbers. To place 3.7 on a number line, students can represent tenths from 3.0 to 4.0. To place 3.55, they must divide the interval between 3.5 and 3.6 into 10 equal parts, with each space representing one hundredth. They can then conclude that (3.55; < 3.7), so Samantha has taken a longer jump than Remi.
Students with good number sense can also compare 3.55 m and 3.7 m by first noticing that they represent 2 jumps greater than 3 m. Then, they can compare tenths to notice that thefirst number has 5 tenths, or 5 decimetres, while thesecond has 7.
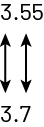
The2nd jump is therefore longer than the1st. Students can also, after comparing ones, think of 3.7 as 3.70, or 3 metres and 70 centimetres. The number 3.55 represents 3 metres and 55 centimetres. The 3.7-metre jump is therefore longer than the 3.55-metre jump.
Traditionally, a procedure was taught where you had to add a 0 to the end of 3.7 to give 2 numbers with the same number of decimal places. The decimal parts, 55 and 70, were then compared to conclude that 3.70 was greater than 3.55. Although the teaching of the method was accompanied by an explanation, so much emphasis was placed on the procedure that the explanation and the concept were quickly lost. Not surprisingly, young people often answered such questions incorrectly. For example, in an international test ofsixth graders, 87% reported that 6 987 is greater than 6 879, while only 52% concluded that 1.05 is greater than 1.015 (Brissiaud, 1998). Students who understand the concept of place value do not need to apply a procedure to compare decimal numbers.
Open problems, which offer more than one answer and are thought-provoking, allow students to deepen their understanding of order relationships.
- Determine three decimal numbers between \(\frac{1}{4}\) and \(\frac{1}{2}\).
- Determine three decimal numbers between 0.5 and 0.6.
- Determine three numbers within 1 tenth of 2.8.
Source: Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 54-55.
Knowledge: Set of Decimal Numbers (ⅅ)
The set of decimal numbers is made up of all numbers that have a decimal point, (for example, 3.72; 0; 12.13564). This set includes all integers, because they can be expressed with a decimal part (for example, 3 = 3.0). It also includes all fractions (for example, \(\frac{2}{5}\; = \ ;0.4\), \(\frac{3}{{16}}\; = \;0.187\;5\), ( \(\frac{1}{3}\; = \;0.333\;3 \ldots \;{\rm{et}}\;\frac{7}{{11}}\; = \;0.636\; 363 \ldots \)).
It is interesting to note that all decimal numbers that terminate can be expressed as decimal fractions, that is, fractions whose denominator is a power of 10. Be cautious if introducing this to students, however, since this property is NOT true for the infinite repeating decimal numbers and infinite non-repeating decimal numbers they will see later on in their math studies.
Examples
\(3.72\; = \;3\frac{{72}}{{100}}\; = \;\frac{{372}}{{100}}\)
\( - 5.1\; = \; - 5\frac{1}{{10}}\; = \; - \frac{{51}}{{10}}\)
\(5\; =\; 5.0 = \frac{5}{1}\)
Since all whole numbers are integers and all integers are decimal numbers, we can represent the relationship between the sets of numbers by the Venn diagram below.
Note: A decimal number can be a terminating decimal number (for example, 0.45), a repeating non-terminating decimal number (for example, 0.333…) or a non-repeating non-terminating decimal number (for example, 3.14159…).
Source: Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 42.
Knowledge: Set of Rational Numbers (ℚ)
The set of rational numbers includes all numbers that can be expressed in fractional form. It includes whole numbers, integers, terminating decimal numbers, as well as numbers whose decimal expression is infinite and periodic (for example, \(\frac{1}{3}\; = \;0,333\;33...\; = \;0,\overline 3 \); \(\frac{5}{{11}}\; = \;0,454\;545...\; = \;0,\overline {45} \); \( -\frac{{421}}{{198}}\; = \; - 2,126\;262...\; = \; - 2,1\overline {26} \)). We can represent the relationship between the sets of numbers by the Venn diagram below.
Source: Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 43.