B1.6 Round decimal numbers to the nearest tenth, hundredth, or whole number, as applicable, in various contexts.
Skill: Rounding Decimal Numbers in Various Contexts
In most real-life situations, it is not necessary to work with a precise number, since an approximation is just as valid and often more convenient. Intermediate students need to be able to round using their number sense, which requires analysis and reflection.
A number can be rounded to a pre-determined position value. For example, when purchasing an item for $11.34, the provincial sales tax of 8% is calculated to be $0.907 2. However, we will pay $0.91 because the amount is always rounded to the nearest hundredth of a dollar since thousandths and 10 thousandths of a dollar are not part of our coins.
Students should be presented with a variety of problems that encourage them to think about the effect of rounding on quantity and to choose how to round. Should they round to the nearest one, the nearest tenth, or the nearest hundredth? The choice depends on the context, the meaning of the number and the reasons for rounding. For example, a restaurant owner who has tables that are 2.27 m long may, when purchasing tablecloths, round the length to 2.3 m or even 2.5 m to be sure that the tablecloths purchased will be long enough. However, when talking to her employees, she can refer to it as the 2 m table. In short, it is only after an analysis of the context that one can determine how to do the rounding or at what position the rounding should be done.
Unfortunately, rounding is too often taught using methods that are meaningless because they deal with numbers and not quantity. For example, to round a decimal number to the nearest tenth, students are taught to identify the digit in the position to be rounded and then consider the digit that follows it. If it is greater than or equal to 5, the identified digit is increased by one and the digits that follow are eliminated.
Example
Note: Since rounding a decimal number requires students to use their decimal number sense, it is important that they have had the opportunity to develop it by representing decimal numbers, placing them on a number line and comparing them.
Example
To round 6.28 to the nearest unit, students recognize that 6.28 is a quantity equivalent to 6 and a bit more. They then know that the number is between 6 and 7. They use their number sense to determine whether 6.28 is closer to 6 or 7. For example, they may use a benchmark number representing the middle of the range (6.5 or 6.50), "see" that 6.28 is close to 6.2 or 6.3, or even visualize where 6.28 is on a number line.
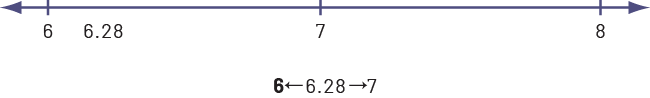
Regardless of which element of number sense chosen, students are then able to round 6.28 to 6.
If they decide to round to the nearest tenth instead, they must use their understanding of the quantity represented by this number and recognize that 6.28 represents a quantity between 6.2 and 6.3.
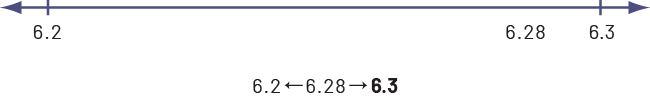
By visualizing the number 6.28 on a line, students can conclude that 6.28 is closer to 6.3 than to 6.2 and therefore, round 6.28 to 6.3.
Source: Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 43-44.