B2.1 Use the properties and order of operations, and the relationships between operations, to solve problems involving whole numbers, decimal numbers, fractions, ratios, rates, and percents, including those requiring multiple steps or multiple operations.
B2.1 Use the properties and order of operations, and the relationships between operations, to solve problems involving whole numbers, decimal numbers, fractions, ratios, rates, and percents, including those requiring multiple steps or multiple operations.
Skill: Using the Properties of Operations
Most of the mathematics content related to Number in grades 7 to 10 can be addressed with the goal of developing algebraic thinking. Instead of asking students to memorize rules for performing operations on different numbers, it is more effective to "[…] move them beyond these particular cases and come to think about the underlying mathematical generalization (Beatty & Bruce, 2012; Ontario Ministry of Education, 2013, p. 6). The goal is to have students observe and analyze a situation, as well as make various connections in order to formulate a generalization. Understanding properties such as commutative, associative and distributive properties in Number is a prerequisite for simplifying algebraic expressions and solving equations. Simplifying and solving equations also requires an understanding of the meaning of an equality situation and the meaning of the equal sign.
Exploring the various properties of operations means examining the relationships between numbers, that is, analyzing situations in which the change of one quantity produces an effect on another quantity.
Most of the mathematics content related to Number in grades 7 to 10 can be addressed with the goal of developing algebraic thinking. Instead of asking students to memorize rules for performing operations on different numbers, it is more effective to […] move them beyond these particular cases and come to think about the underlying mathematical generalization (Beatty & Bruce, 2012; Ontario Ministry of Education, 2013, p. 6). The goal is to have students observe and analyze a situation, as well as make various connections in order to formulate a generalization. Understanding properties such as commutative, associative and distributive properties in Number is a prerequisite for simplifying algebraic expressions and solving equations. Simplifying and solving equations also requires an understanding of the meaning of an equality situation and the meaning of the equal sign.
Exploring the various properties of operations means examining the relationships between numbers, that is, analyzing situations in which the change of one quantity produces an effect on another quantity.
Commutative Property of Addition and Multiplication
When two numbers are added or multiplied, the result is the same, even if the order of the numbers being added or multiplied is changed.
The student who makes this generalization understands the commutative property. This understanding helps them simplify algebraic expressions and solve equations. However, a student who does not understand the commutative property will perform addition or multiplication instead of comparing the terms on either side of the equal sign.
When two numbers are added or multiplied, the result is the same, even if the order of the numbers being added or multiplied is changed.
The student who makes this generalization understands the commutative property. This understanding helps them simplify algebraic expressions and solve equations. However, a student who does not understand the commutative property will perform addition or multiplication instead of comparing the terms on either side of the equal sign.
| ADDITION | MULTIPLICATION |
|---|---|
|
|
QUESTIONING
What do you notice about the order of the terms?
Do you think that changing the order of the terms changes the solution? How can you justify this?
Are the equalities in examples a) true? How do you know?
How did you determine the value of y in examples b)?
Have you thought of a strategy to verify your answer?
In both examples c), how did you use the commutative property to simplify the expressions?
Associative Property
When numbers are added or multiplied, they can be grouped in various ways without changing the result of the operation. The student who makes this generalization understands the associative property where the order of the numbers is maintained, but the brackets are moved. Understanding this property allows students to simplify algebraic expressions and solve equations.
When numbers are added or multiplied, they can be grouped in various ways without changing the result of the operation. The student who makes this generalization understands the associative property where the order of the numbers is maintained, but the brackets are moved. Understanding this property allows students to simplify algebraic expressions and solve equations.
| ADDITION | MULTIPLICATION |
|---|---|
|
\((40\; + \; - 5)\; + \; - 30\; = \;40\; + \;( - 5\; + \; - 30)\) \((2x + \; - 3)\; + \; - 4 = 2x + \;( - 3 + \; - 4)\) |
\((10\; \times \; - 2)\; \times \;5\; = \;10\;( - 2\; \times \;5)\) \((3x \times \; - 2)\; \times \;4\; = \;3x\;( - 2\; \times \;4)\) |
QUESTIONING
What are you comparing when you look for equality?
Explain how the original expressions are changed.
What do you notice about the order of the terms in these examples?
Do you think the move of the brackets change the solution? Justify your thinking.
Distributive Property
The distributive property of multiplication over addition or subtraction is a property that transforms a product of sums or differences to a sum or difference of products. The student who makes this generalization understands that it is possible to distribute terms in different ways, that is, to decompose numbers and get the same result.
The problem below is a typical example of what can be presented to the student to help them understand the distributive property of multiplication.
The distributive property of multiplication over addition or subtraction is a property that transforms a product of sums or differences to a sum or difference of products. The student who makes this generalization understands that it is possible to distribute terms in different ways, that is, to decompose numbers and get the same result.
The problem below is a typical example of what can be presented to the student to help them understand the distributive property of multiplication.
Example
An auditorium contains 16 rows of 34 seats. How many seats are there in the auditorium?
The use of the context of an auditorium is no coincidence. This is a good context for exploring the area model.
A well-orchestrated instructional sequence supports students to use an area model:
- using concrete materials (for example, base ten blocks, algebra tiles);

- using semi-concrete materials (for example, grid paper)
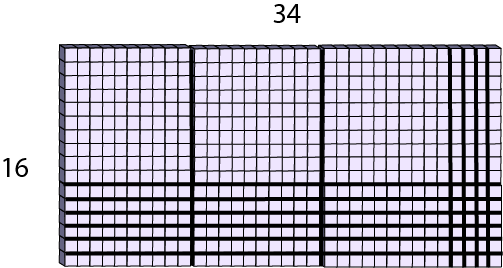
- using a more abstract representation (for example, area model).

The strategy related to the concept of area that involves making sums of partial products helps the student generalize and discover the distributive property of multiplication over addition.
This learning is useful in different grades, as the area model can be applied to multiplication in other number systems (for example, fractions, decimal numbers), as well as to algebraic situations.
The strategy related to the concept of area that involves making sums of partial products helps the student generalize and discover the distributive property of multiplication over addition.
This learning is useful in different grades, as the area model can be applied to multiplication in other number systems (for example, fractions, decimal numbers), as well as to algebraic situations.
| MULTIPLICATION OF FRACTIONS | MULTIPLICATION OF ALGEBRAIC EXPRESSIONS |
|---|---|
|
Calculate \(4\frac{1}{2}\; \times \;8\frac{1}{4}\). |
Simplify \((x + \;3)(x + \;2)\). |
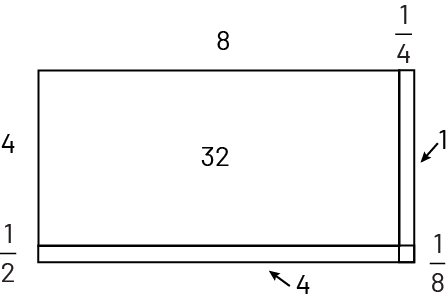 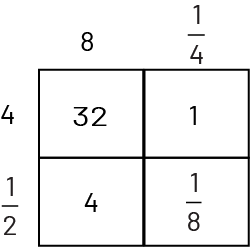 |
  |
| \(\begin{array}{l}\quad 4\frac{1}{2}\; \times \;8\frac{1}{4}\\ = \;(4\; \times \;8 )\; + \;(4\; \times \;\frac{1}{4})\; + \;(\frac{1}{2}\; \times \;8)\; + \; (\frac{1}{2}\; \times \;\frac{1}{4})\\ = \;37\frac{1}{8}\end{array}\) | \(\begin{array}{l}\quad (x\; + \;3)\; \times \;(x\; + \;2)\\ = {x^2}\; + \;3x \; + \;2x\; + \;6\\ = \;{x^2}\; + \;5x\; + \;6\end{array}\) |
|
QUESTIONING How does the area model facilitate the multiplication of fractions? How did you determine where to place the whole numbers (4, 8) and the fractions \(\frac{1}{2}\text{,}\;\frac{1}{4}\)? How did you determine the numbers in the boxes? |
QUESTIONING
How does the area model help you understand the multiplication of binomials? How did you determine where to place each term of the binomials? How do you get the expressions in the boxes? |
It is important for students to explore in parallel whether the commutative, associative and distributive properties apply to subtraction and division. The associative and commutative properties do not apply to subtraction or division. The distributive property does not apply to division.
It is important for students to explore in parallel whether the commutative, associative and distributive properties apply to subtraction and division. The associative and commutative properties do not apply to subtraction or division. The distributive property does not apply to division.
| SUBTRACTION | DIVISION | |
|---|---|---|
| Associative Property | \(\ (a\; - \;b \; )\; - \;c\; \ne \;a\; - \;(b\; - \;c \; )\)
\(\ (10\; - \;2 \;)\; - \;3\; \ne \;10\; - \;(2\; - \;3\;)\) \(\ 5\; \ne \;11\) |
\(\ (a\; \div \;b\;)\; \div \;c\; \ne \;a\; \div \;(b\; \div \;c\;)\) \(\ (48\; \div \;4 \;)\; \div \;2\; \ne \;48\; \div \;(4\; \div \;2 \;)\) \(\ 6\; \ne \;24\) |
| Commutative Property | < >\(\ a\; - \;b\; \ne \;b\; - \;a\)< >\(\ 36\; - \;27\; \ne \;27\; - \;36\) | \(\ a\; \div \;b\; \ne \;b\; \div \;a\)
\(\ 120\; \div \;5\; \ne \;5\; \div \;120\) |
| Distributive Property | \(\ a\; \div \;(b\; + \;c \; )\; \ne \;(a\; \div \;b \; )\; + \;(a\; \div \;c \;
)\)
\(\ 24\; \div \;(4\; + \;8 \;)\; \ne \;(24\; \div \;4 \;)\; + \;(24\; \div \;8 \;)\) \(\ 24\; \div \;12\; \ne \;6\; + \;3\) \(\ 2\; \ne \;9\) |
Algebraic Generalizations
The student should master the following algebraic generalizations related to the properties of real numbers.
Commutative Property
For all a and b elements of ℝ (real numbers), \(a + b = b + a\)
For all a and b elements of ℝ (real numbers), \(a \times\; b\;=\; \;b \times\;a\)
Associative Property
For all a, b and c elements of ℝ (real numbers), \((a + b) + c = a + (b + c)\)
For all a, b and c elements of ℝ (real numbers), \(\left( {a\; \times \;b \;} \right)\; \times \;c\; = \;a\; \times \;\left( {b\; \times \;c\;} \right)\).
Distributive Property
For all a, b and c elements of ℝ (real numbers), \(a \; \left( {b\; \;+ \;c\;} \right)\; = \;ab\; + \;ac\).
Identity Rule
For all a elements of ℝ (real numbers), \(a\; + \;0\; = \;0\; + \;a\; = \;a\).
Identity Principle of Multiplication: For all a elements of ℝ (real numbers), \(a \times \;1 = \;1 \times \;a = \;a\).
Zero Property of Multiplication
For all a elements of ℝ (real numbers), \(a \times \;0\; = \;0\; \times \;a = \;0\).
Source: translated from Guide d'enseignement efficace des mathématiques de la 7e à la 10e année, Fascicule 2, Algèbre, p. 18-25.
Skill: Using the Order of Operations
The order of operations can arise in a problem-solving context or in operations presented as context-free numeric expressions.
In the classroom, it is more important to focus on the meaning of expressions in a problem-solving context than on the ability to evaluate expressions with multiple operations.
Operations in a Problem-Solving Context
To solve a problem involving a series of operations, the order to be followed is dictated by the meaning of the problem.
Example 1
Simon has 3 envelopes containing 5 stamps each and his sister Annabelle has 7 envelopes containing 4 stamps each. They decide to put all their stamps together to form a larger collection. How many stamps are in their joint collection?

To solve this problem logically, students must first determine the number of stamps in Simon's collection (\(3\; \times \;5\; = \;15\)), then the number of stamps in Annabelle's collection (\(7\; \times \;4\; = \;28\)). Then they have to find the total number of stamps in the 2 collections (\(15\; + \;28\; = \;43\)). Here, multiplication takes precedence over addition.
To represent all these operations in a single numerical expression, we could write \(3 \times \;5 + \;7 \times \;4 \). However, this expression can be confusing. That's why it's better to use brackets to specify the order in which the operations must be performed, that is, (\(3\; \times \;5)\; + \;(7\; \times \;4)\). The solution can then be presented as follows:
\(\begin{align} (3\; \times \;5)\; + \;(7\; \times \;4)\; &= \;15\; + \;28\\ &= \;43\end{align}\)
So, their combined collections contain 43 stamps.
In the following example, it is possible to solve the problem by giving priority to addition over multiplication.
Example 2
Alphonse orders 12 comic books at a cost of $7 each. There is a $2 delivery charge per book. How much do the 12 books cost him?
Students can first determine the price of each book (\( \$7\; + \$2\; = \$9 \)), then the total cost (\(12\; \times \; \$9\;=\;\$108\;\)). As in the previous example, it is possible to present the two operations with brackets in the same numerical expression: \((7\; + \;2)\; \times \;12\) or \(12\; \times \;(7\; + \;2)\).
Thus, parentheses allow you to group certain elements of a numerical expression and to specify that these elements must be processed first.
Operations in the Form of Numerical Expressions
Ideally, numerical expressions should be presented in a context that helps establish the order of operations. However, there are times when a numerical expression must be evaluated out of context. As presented earlier, brackets help prioritize the operations to be performed, as in the numerical expressions \((3 \times \;5)\; + \;(7 \times \;4)\) and \(12 \times \;(7 + \;2)\). However, a numerical expression presented without brackets and without context could generate a multitude of responses. For example, one might decide to treat the operations in the order in which they appear:
\(\begin{align}3\; \times \;5\; + \;7\; \times \;4\; &= \;15\; + \;7\; \times \; 4\\ &= \;22\; \times \;4\\ &= \;88\end{align}\)
We could also decide to give priority to addition over multiplication:
\(\begin{align}3\; \times \;5\; + \;7\; \times \;4\; &= \;3\; \times \;12\; \times \;4\\ &= \;36\; \times \;4\\ &= \;144\end{align}\)
When faced with a numerical expression of this kind, certain rules have been established to remove any ambiguity and to standardize its treatment. One of these rules is that multiplication and division are performed before addition and subtraction. In this context, the agreed way to evaluate the previous expression is:
\(\begin{align}3\; \times \;5\; + \;7\; \times \;4\; &= \;15\; + \;28\\ &= \; 43\end{align}\)
The acronym BEDMAS is often presented to students to help them remember the set of rules that define the order of operations. The "B" stands for the brackets that should be processed first. The "E" stands for exponents that are evaluated next. The "D" and "M" represent division and multiplication, operations to be performed in the order in which they appear. Finally, addition and subtraction correspond to the letters "A" and "S". These two operations are performed last according to the order in which they appear. The order of operations is part of the Grade 6 curriculum, but students in other grades may approach these rules informally. It is only in the intermediate grades that exponents are introduced. In the classroom, it is more important to focus on the meaning of expressions in a problem-solving context than on the ability to evaluate expressions with multiple operations.
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 1, Nombres naturels, p. 108-110.
Some calculators respect the order of operations, while others do not (for example, if the keys \(3\; + \;4\; \times \;5\; = \) are pressed, a calculator that respects the order of operations would display 23, while a calculator that does not respect it would display 35). Students must then know the characteristics of their calculator, as well as the order of operations, so as to change the order of operations if necessary (for example, the keys would have to be pressed as \(3\;\;(4\; \times \;5)\; = \) or \(4\; \times \;5\; + \;3\; = \) to get the correct answer on a calculator that does not respect the order of operations).
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 1, Nombres naturels, p. 120.
Skill: Using Relationships Between Operations
Understanding the properties of operations and the relationships between them allows for more flexible use.
In the primary grades, students have made connections between operations through various activities. For example, they know that addition and subtraction are inverse operations and that addition is commutative. Over time, they develop their number and operation senses and gradually use them before performing operations. This practice, while often informal and mental, is still essential to understanding the relationships between numbers and between operations.
- Addition and subtraction are inverse operations.
- Multiplication and division are inverse operations.
- Multiplication can be associated with repeated addition.
- Division can be associated with repeated subtraction.
- Addition and subtraction are inverse operations.
- Multiplication and division are inverse operations.
- Multiplication can be associated with repeated addition.
- Division can be associated with repeated subtraction.
The fundamental operations of addition, subtraction, multiplication and division are closely related despite their apparent differences. The more opportunities students have to work with the operations, the more they can notice and understand the connections between them.
Addition and Subtraction
There are four types of problems in addition and subtraction: changing (joining or separating), combining (part-part-whole) and comparing problems. In order for students to understand the connections between quantities in each of these cases, it is important that they be presented with a variety of problem types. The following table presents a variety of addition and subtraction problems.
Addition and subtraction are operations that can be used to solve problems. It is important to avoid referring to problems as "subtraction problems" or "addition problems" because it is the understanding of the situation that leads to the choice of a problem-solving strategy, in this case the choice of using addition or subtraction to solve it. Thus, students must analyze the problem, choose a strategy and apply it, just as adults do. In this context, the teacher's role is to assist students in their analysis and understanding of operations.
It is important to note that the problems in the table appear similar because of their context. However, for students, each situation represents a particular problem. It is through experience with these different types of problems that students will become proficient with addition and subtraction.
Types of Addition and Subtraction Problems

Also known as "Change Problems", joining and separating problems are perceived by students as active situations, easier to model and "see" as the start quantity increases or decreases. Combining and part-part-whole problems, however, assume a static situation, as no action or change occurs, making them more abstract and difficult to understand. Comparing problems, on the other hand, deal with the relationship between two quantities by contrasting them: so there is no action, but a comparison of one quantity to another to find the difference between them.
Since students are regularly exposed to problems where the result or final quantity is sought, they find these kinds of problems easier to solve. They have more difficulty solving problems where the start quantity or change (joined or separated) is unknown. Therefore, working with these kinds of problems will support the development of a more solid understanding of addition and subtraction and the connections between them. For example, in addition problems where the unknown value is the start quantity, students more easily see the benefits of addition (for example, \(?\; + \;12\; = \;37 \)) which makes it possible to respect the order in which the action takes place in the problem. This allows them to use a strategy (for example, counting or counting down) to determine the initial quantity. These students demonstrate their understanding of the problem and their ability to use a strategy to solve it. However, they do not demonstrate an understanding of the meaning of difference (and subtraction). If they had used subtraction, that is \(37\; - \;12\; = \;?\), they would have demonstrated a broader understanding of the relationships between these operations. When students are learning, there is no need to impose a strategy on them. The obligation to subtract will not help students who do not see the relevance of this strategy. However, if they regularly experience a variety of problems and participate in the mathematical discussions that follow, they can begin to see the connections between various strategies and will eventually adopt new ones. They then become more efficient.
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 1, Nombres naturels, p. 81-84.
To understand multiplication and division, one must recognize the three types of quantities involved: the total quantity (for example, 8 flowers), the number of equal groups (for example, 4 pots) and the size of each group (for example, 2 flowers per pot).
In problems presented to students, division is too often associated with only one type, namely equal-sharing (partitive division). Equal-grouping (quotative division) is usually neglected. With partitive division, the total quantity and the number of groups are known (for example, 3 students want to share 15 apples equally and we are looking for the number of apples each person will receive).

With quotative division the total quantity and the size of the groups are known (for example, we have 15 apples and we want to put them in bags, 3 apples per bag; we look for the number of bags we need).

It is essential that students have experience with both types of division problems, as they will develop a deeper understanding of the operation, which is fundamental to many other mathematical concepts. It is not necessary for students to know the names of the problem types, but it is essential that they have the opportunity to solve a variety of problem types while using a variety of strategies.
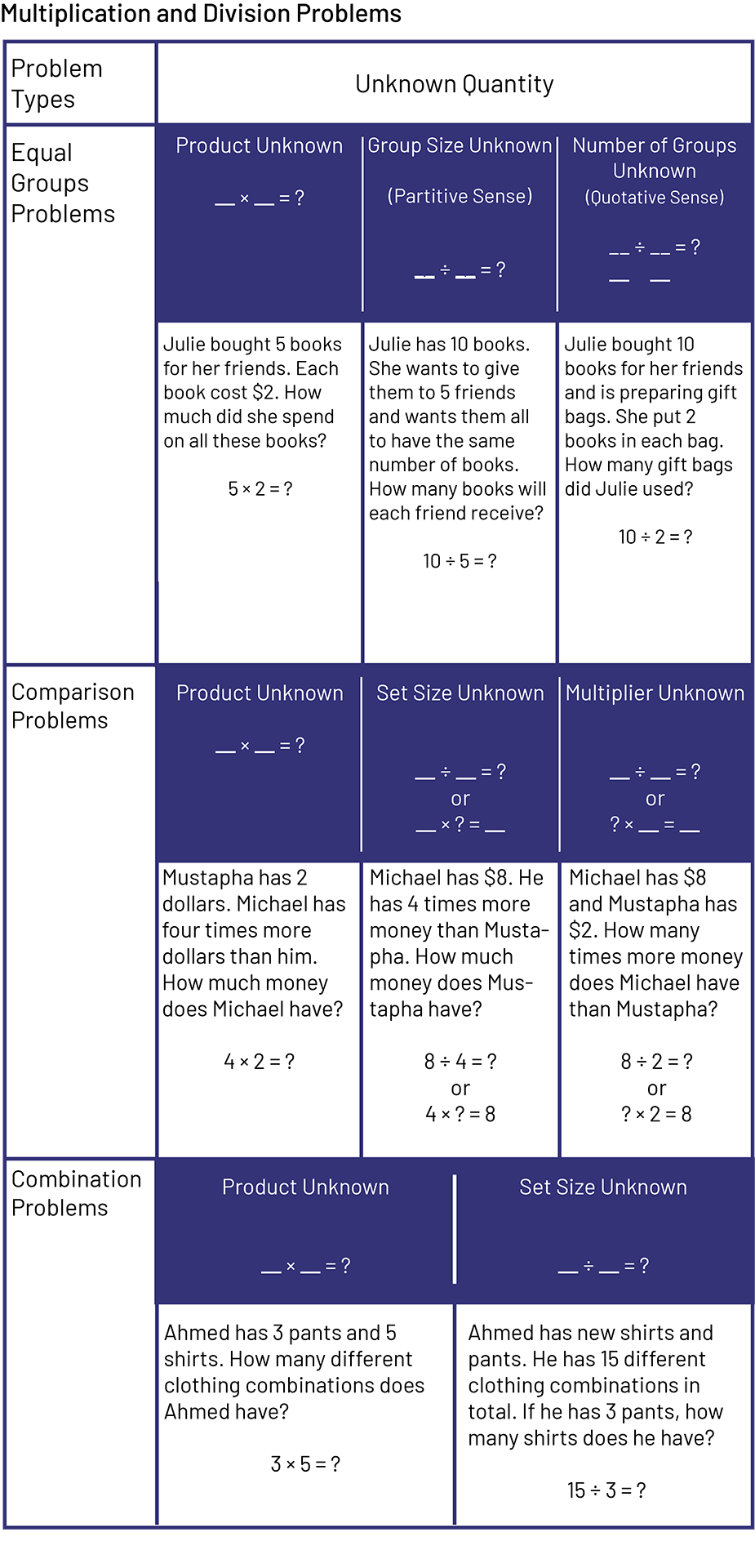
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 1, Nombres naturels, p. 84-86.
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 1, Nombres naturels, p. 84-86.
Effect of Operations
Each operation has an effect on the quantities involved. Depending on the operation, certain quantities increase or decrease. They may increase or decrease by a lot or a little. Tracking the effect of operations on numbers allows students to make connections between operations and to anticipate the result of an operation. For example, if we subtract 8 from 160, we will notice little effect because the difference between 160 and 152 is relatively small. However, if we divide 160 by 8, the effect is large, because the resulting quotient, 20, is much smaller than 160. We can also compare the effect produced by addition to that produced by multiplication. Compared to multiplication, addition increases a number by a small amount. For example, when 160 is multiplied by 8, you get 1280, whereas if you add 8, you get 168. People with good operations sense recognize the effect of operations on whole numbers, but students are often impressed by the effect of, for example, multiplication. One caveat is that care must be taken when generalizing, as operations on decimal numbers or fractions may have different effects than those on whole numbers. In some cases, the effect may even be the opposite. For example, if a whole number is multiplied by another whole number, the product is larger than the two factors (for example, if 3 is multiplied by 6, the product 18 is larger than 6 and 3), whereas if a proper fraction is multiplied by a whole number, the product is smaller than one of the two factors (for example, if \(\frac{1}{2}\) is multiplied by 6, the product 3 is smaller than 6).
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 1, Nombres naturels, p. 90-91.
Skill: Solving Problems Requiring Multiple Operations
Whether it is a problem with one operation or multiple operations, students must make decisions and choices based on the context. A problem-solving approach will introduce them to this thinking. When faced with a problem, they must first analyze it to determine the data and understand that a calculation must be performed. Then, depending on the context, one must know whether one is looking for an approximate or an exact answer. In both cases, depending on the context and the numbers involved, it is then necessary to determine whether the calculation will be performed mentally, in writing or using a calculator. Finally, the desired calculation is performed.
Diagram of the Students' Thinking About a Problem
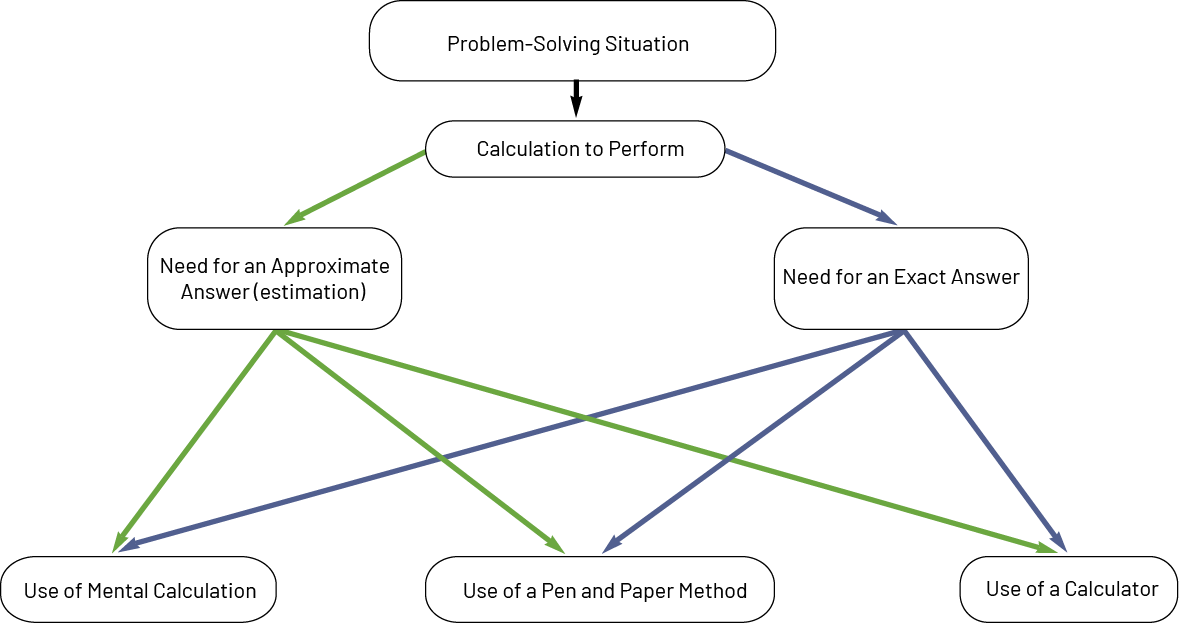
Knowledge: Properties of Operations
Properties of operations are characteristics that are unique to operations, regardless of the numbers involved.
The properties of the operations are:
- Commutative Property \((3\; + \;5 \;=\; 5\; +\; 3)\)
- Associative Property: \((2\; + \;9)+ \;11 \;=\; 2\; +\;(9\; + \;11)\)
- Distributive Property: \((8\; \times \;7) = (8\; \times \;5) + (8\; \times \;2)\)
- Identity Principle: \(13\; + \;0\; = \;13\), \(0\; + \;13\; = \;13\); \(25\; \times \;1\; = \;25\), \(1\; \times \;25\; = \;25\)
- Zero Property of Multiplication: \((8\; \times \;0) = 0\)
Knowledge: Commutative Property
An operation is commutative if its result remains unchanged when the order of its terms is reversed. Addition and multiplication are commutative. For example, \(27\; + \;63\; = \;63\; + \;27\) and \(8\; \times \;6\; = \;6\; \times \;8\).
Generalization:
\(\begin{align} a + b &= b + a \\ a \times b &= b \times a \end{align}\)Knowledge: Associative Property
The associative property is a property of addition and multiplication. It allows the terms of an expression to be combined in different ways without changing their value.
Generalization:
\(\begin{align} (a\; + \;b\;)\; + \;c\; &= \;a\; + \;(b\; + \; c\;)\\ ( a\; \times \;b\;)\; \times \;c\; &= \;a\; \times \;(b\; \times \;c\;)\end{align}\)
\(\begin{align} (a\; + \;b\;)\; + \;c\; &= \;a\; + \;(b\; + \; c\;)\\ ( a\; \times \;b\;)\; \times \;c\; &= \;a\; \times \;(b\; \times \;c\;)\end{align}\)
Knowledge: Distributive Property
Multiplication is distributive over addition and subtraction.
The distributive property allows one to perform an operation on a sum or a difference of terms and obtain the same result as if the operation had been performed on each term. For example,
- one can multiply \(3\; \times \;(5\; + \;6)\) and arrive at the same result as if one had performed \((3\; \times \;5)\; + \;(3\; \times \;6)\);
- one can multiply \(3\; \times \;(20\; - \;2)\) as \((3\; \times \;20)\; - \;(3\; \times \;2)\).
Generalization: \(a\; \times \;(b\; + \;c\;)\; = \;(a\; \times \;b\;)\; + \;(a\; \times \; c\;)\)
Knowledge: Zero Property of Multiplication
When multiplying any number by 0, the result is always 0 (for example, \(684\; \times \;0\; = \;0;\;16.67\; \times \;0\; = \;0\)).
Generalization: \(a\; \times \;0\; = \;0\), \(0\; \times \;a\; = 0\)
Knowledge: Identity Principle
The Identity Principle of Addition states that when adding 0 to any amount, the amount stays the same (for example, \(287\; + \;0\; = \;287\); \(4.5\; + \;0\; = \;4.5\; \). The Identity Principle of Multiplication states that when multiplying an amount by 1 or dividing an amount by 1, the amount stays the same (for example, \(133 \times \;1 = 133\); \(432.1\; \times \;1\; = 432.1\)).
Generalization: \(a\; + \;0\; = \;a\), \(a\; - \;0\; = \;a\), \(a\; \times \;1\; = \;a\), \(a\; \div \;1\; = \;a\)
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 1, Nombres naturels, p. 102-107.
Knowledge: Relationships Between Addition, Subtraction, Multiplication and Division
Operation sense involves the ability to represent situations with symbols and numbers. Understanding the meaning of the operations, and the relationships between them, allows one to choose the operation that best represents a situation and allows one to solve the problem most effectively, given the tools available.
- Addition and subtraction are inverse operations.
- Multiplication and division are inverse operations.
- Multiplication can be associated with repeated addition.
- Division can be associated with repeated subtraction.
