B1.1 Represent and compare very large and very small numbers, including through the use of scientific notation, and describe various ways they are used in everyday life.
Skill: Representing Numbers
Students need to learn to represent numbers in a variety of ways and to recognize them in their multiple representations. These skills help them make connections between a number, its representation, and the quantity it represents. It is therefore essential that students be exposed to different representations of numbers. It is also important that they be exposed to a variety of contexts that lead them to represent a number and to move from one representation to another.
Representations Using Words
A number is an abstract representation of a very complex concept. The relationship between the way a number is named and the quantity it represents may not be obvious to students. Many adults mistakenly believe that if students can count, they understand the meaning of each number. However, a student may be able to read and name a number, for example, forty-seven million, without really having an understanding of the quantity it represents.
Source :Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 64-65.
Large numbers can be expressed as decimal numbers by expressing the place value in words. For example, 36.24 trillion, which is equivalent to \(36\;240\;000\;000\;000\; \rm{or}\; 36,24 \times 10^{12}\).
When large numbers are written down, they are sometimes rounded and can be expressed using a combination of numbers and words (for example, 37 020 005 205 becomes 37 billion).
Source : Curriculum de l’Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l’Éducation de l’Ontario.
Symbolic Representations
Numbers are represented symbolically by the digits that make them up. They are written from left to right in 3-digit periods that make up the trillions, billions, millions, thousands and ones. Each of the periods includes hundreds (h), tens (t) and ones (o).
Each period - thousands, millions, billions, trillions - is 1000 times the preceding one.
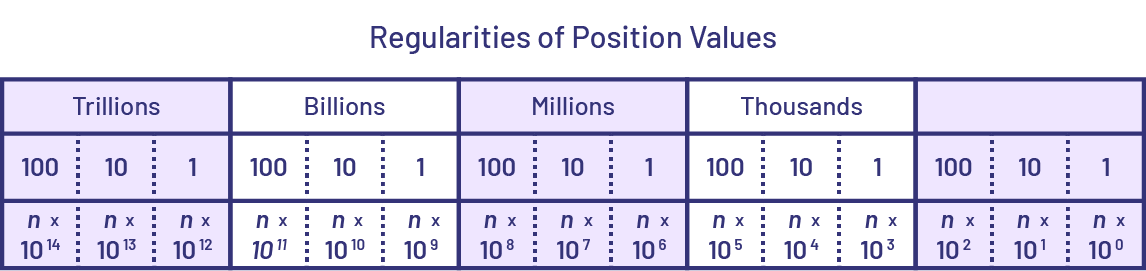
Source: Ontario Curriculum, Mathematics Curriculum, Grades 1-8, 2020, Ontario Ministry of Education.
Notes:
- In French, the term "billion" does not have the same meaning as the English term billion. In French, a billion corresponds to one thousand billion (10 exponent 12) whereas in English it corresponds to one thousand million (10 exponent 9). In other words, the English term billion corresponds to the French term "milliard".
- Note: In English as well as in French, numbers are written by adding a space between the 3-digit periods (for example, 13 567 232). Although writing 4-digit numbers without using a space is accepted (for example, 3543), writing them with a space (for example, 3 543) is preferred.
Source : adapted from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 48, 64-72.
Decimal numbers are used to give greater precision to a rounded number. For example, the number 37 020 005 205 could be written as 37.02 billion.
Sometimes in charts and tables, the unit represents thousands. For example, the number 7.238 billion could be represented by 7238 million.
When a number is expressed in scientific notation, there is only one non-zero digit to the left of the decimal point. Thus, 36.24 × 1012 is not in scientific notation because there are two digits to the left of the decimal point. In scientific notation, 36 240 000 000 000 is written as 3.624 × 1013.
- 57 000 is written \(5.7\; \times \;{10^4}\) and means \(5.7\; \times \;10\; \times \;10\; \times \;10\; \times \;10\);
- 37 billion is written \(3.7\; \times \;{10^{10}}\);
- 21 465 trillion is written \(2.146\;5\; \times \;{10^{13}}\).
Scientific notation also allows very small numbers, such as numbers between 0 and 1, to be represented using negative exponents.
- If a positive exponent indicates how many times to multiply a base by 10, a negative exponent indicates how many times to divide a base by 10.
- For example, light travels one kilometer every 0.000003 seconds, or every 3 millionths of a second. In scientific notation, this number is written \(3\; \times \;{10^{{}^ - 6}}\) and means \(3\; \div \;10\; \div \;10 \; \div \;10\; \div \;10\; \div \;10\; \div \;10\;\).
Source : Curriculum de l’Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l’Éducation de l’Ontario.
Skill: Comparing Numbers
The magnitude of a large number can be understood by comparing it to other numbers and quantities. For example:
- 1 trillion seconds is around 32 000 years;
- 1 million seconds is around 11.5 days;
- 1 billion seconds is around 32 years.
Numbers expressed in scientific notation can be compared by considering the number of times the decimal number is multiplied or divided by ten. The more times it is multiplied by ten, the greater the number. The more times it is divided by ten, the smaller the number.
Source: Ontario Curriculum, Mathematics Curriculum, Grades 1-8, 2020, Ontario Ministry of Education.
For example, in astronomy, the distance between Saturn and the Sun is 837 000 000 km and the distance between Neptune and the Sun is 4.48 billion km. In order to compare these distances, the student must first be able to read the numbers presented and then choose the representation that will facilitate this comparison. Here, the student could write these numbers in scientific notation and then compare them.
Distance between Saturn and the Sun \( = \;8.37\; \times \;{10^8}\;{\rm{km}}\)
Distance between Neptune and the Sun \( = \;4.48\; \times \;{10^9}\;{\rm{km}}\)
This will make it easier for students to compare the numbers by noticing that the distance between Neptune and the Sun is greater, since the power of 10 is raised to the exponent 9 as opposed to the exponent 8 for the distance between Saturn and the Sun.
Comparing quantities and describing their differences or similarities helps to understand the order of magnitude of a number, or "how much" it is.
Source : Curriculum de l’Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l’Éducation de l’Ontario.
Skill: Describing Ways in Which Very Large Numbers and Very Small Numbers are Used in Everyday Life
Real-life contexts can provide an understanding of the magnitude of large and small numbers.
Source: Ontario Curriculum, Mathematics Curriculum, Grades 1-8, 2020, Ontario Ministry of Education.
Context is all the information surrounding a given situation. This information helps to identify the situation in which the quantities are used and facilitates the exercise of a critical eye on the numbers in question. In addition, the context facilitates the establishment of relationships between numbers, mathematical concepts and the mathematical world. For all these reasons, the exploration of mathematics in problem-solving situations is advocated.
What does 2 000 000 000 (two billion) mean exactly? We are talking about 2 000 000 000 "what"? In short, a number without context has little meaning. Therefore, it must be accompanied by units (2 000 000 000 people, dollars,km2…) if it is to be understood. Students in the primary division have already done number activities in a variety of contexts using a variety of units. In the junior and intermediate divisions, this contextualization needs to be maintained in order to develop a sense of quantity with very large and very small numbers.
An important step to take is to get students to understand that the same number represents the same quantity even though the contexts are different. The number is only a symbolic representation of the quantity. If a province has a debt of $3 000 000 000, or a colony has 3 000 000 000 ants, or a country has 3 000 000 000 trees in its territory, the quantity does not change. Yet, if students are asked if they think there are more ants than trees, many are likely to answer that there are more trees. They focused on the space occupied by the objects rather than the quantity of objects (3 000 000 000).
Students should also recognize that depending on the context of the given situation, different interpretations can be made of the same quantity. For example, for young people, $10 000 000 000 ($10 billion) may represent an unimaginable amount of money. However, in context, the meaning of the number invites nuance: this number represents a huge amount of money for a family, but if this $10 000 000 000 is equivalent to the total year-end debt in Canada, this number in this context represents a lesser amount, at first glance. The context changes, but the quantity remains the same. Similarly, 100 000 blocks of wood is a lot of blocks, while 100 000 hairs on the head is the equivalent of an average head of hair. Or, students may consider that 13 is not a large quantity, but if we add that it is the number of our brothers and sisters, it takes on a whole new value. These simple, concrete examples encourage students to think about and critically analyze quantities.
In the junior and intermediate divisions, understanding numbers in context becomes increasingly important. Students need to begin to make critical judgments about quantities and to exercise discernment about numbers. Learning activities should therefore help students develop other skills, such as recognizing the reasonableness of a given number, recognizing that it is an exact value, or recognizing that it is an approximate number resulting from estimation or even rounding. The development of these skills can be initiated by having class discussions about the meaning of numbers from newspapers and/or scientific journals and discussing their actual meaning and relevance.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 31-32.
In grade8 , students become familiar with very small numbers and very large numbers. It should be noted that learning and discovering very small and very large numbers is very abstract for students. Therefore, it is essential to have students describe their uses, for example, in fields and contexts where these numbers become necessary or even essential (for example, in astronomy, molecular biology, global economics, virology, etc.). In addition, students will be expected to make critical judgments about the representation (numbers expressed in words, in standard notation, in expanded form using powers of 10, in scientific notation) that is most appropriate for a given context.
Example
- The mass of a human cell (fibroblast) weighs 2.3 nanograms, which is equivalent to 2.3×10-12 kilograms.
- As of the 2021 census, Canada's population was just over 38 million people.
Knowledge: Scientific Notation
When a number is expressed in scientific notation, there is only one non-zero digit to the left of the decimal point. Thus, 36.24 × 1012 is not in scientific notation because there are two digits to the left of the decimal point. In scientific notation, 36 240 000 000 000 is written as 3.624 × 1013.
- The number 1 in scientific notation is \(1; \times \;{10^0}).
- The base 10 exponent in scientific notation indicates the number of times the decimal number is multiplied or divided by 10, not the number of zeros that must be included for a number to be written in standard notation.
Source: Ontario Curriculum, Mathematics Curriculum, Grades 1-8, 2020, Ontario Ministry of Education.
Very small numbers can also be represented using scientific notation. Using patterns and prior knowledge, teachers can encourage students to extend a pattern such as the following:
\(\begin{array}{l}{10^3}\; = \;1\;000\\{10^2}\; = \;100\\{10^1}\; = \;10\\{10^0}\; = \;?\\{10^{{}^ - 1}}\; = \;?\\{10^{{}^ - 2}}\; = \;?\\{10^{{}^ - 3}}\; = \;?\end{array}\)
The student will quickly notice that as the exponent becomes smaller, the number quickly becomes smaller. The negative exponent leads to a division by 10 n or a multiplication by a decimal number following this same mathematical pattern. This pattern is understood when the student makes connections between the different ways of writing this number and allows them to see the equivalences between the notations.
Example
\({10^{{}^ - 2}}\; = \;0,01\; = \;\frac{1}{{100}}\; = \;\frac{1}{{{{10}^2}}}\; = \;1,0\; \times \;{10^{{}^ - 2}}\)