GEEM - Skills and Knowledge

E2.2 Explain the relationship between centimetres and metres as units of length, and use benchmarks for these units to estimate lengths.

Skill: Explaining the Relationship Between Centimetres and Metres as Units

The metric standard units associated with the attribute length are derived from system of units that are related by factors of powers of ten. This mathematical fact is used to establish equivalence relationships between these units. For example, exploring length activities that lead students to discover the inverse relationship between the centimetre and the metre will later lead to describing the generalization that there are always 100 centimetres in a metre.

Source: translated from Guide d'enseignement efficace des mathématiques de la maternelle à la 3^e année, Mesure, p. 64.

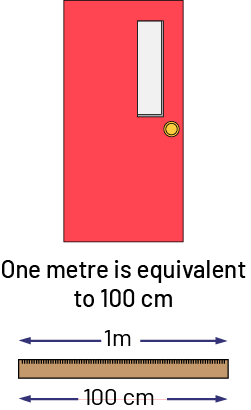
Standard units allow measurements to be reliably communicated. The centimetre and metre are standard metric units of length. There are 100 centimetres in 1 metre.
The measurement of a continuous quantity, such as length, is always approximate. The smaller the unit used, the more accurate the measurement will be. If units of different sizes are used to obtain a more accurate measurement of an object, each unit is counted and treated separately.
For example, to measure a length between 1 metre and 2 metres, one could use a combination of metres and centimetres or just centimetres, or round the measurement to the nearest metre.

Remarks:

In Grade 2, students do not use decimal numbers to measure.
When you have familiar benchmarks for centimetres and metres, it is easier to estimate the length of objects.

Source: The Ontario Curriculum. Mathematics, Grades 1-8, Ontario Ministry of Education, 2020.

Skill: Use Benchmarks for Lengths

Developing a sense of measurement requires the development of very important skills such as benchmarking, estimating, visualizing, problem solving, reasoning, and communicating.

In measurement, benchmarks are mental images that represent non-standard or standard units according to a given or personal reference.

A box that reads, "What do you think of when you imagine a distance of 400 meters?" ("Open parenthesis") It's a lap around the high school track next door ("Close parenthesis")

While the benchmark may vary from person to person, all of them have a special meaning to the person using them to estimate a measurement.

Example

A student can use the length of their toy car as a meaningful benchmark for estimating the size of various familiar objects, and can then associate the appropriate length of 15 centimetres with it.

A student's face associated with a bubble. The bubble reads, "My lunch box is about three car lengths long. There is also a representation of the lunch box, and the three small cars that were used as unconventional units of measurement.

Progression in the Use of Benchmarks

As students explore in measurement, they learn to make increasingly complex and abstract use of benchmarks. According to Joram (2003, pp. 65-66), this progression is characterized by three levels, and teachers need to help students move through each level.

At the first level, as illustrated in the previous example, students use objects or manipulatives as both benchmarks and non-standard units. This use of concrete benchmarks is essential to the construction of a reference point and is well suited to students in the primary grades, when their ability to construct and maintain accurate mental images is developing. At this level, students can also use concrete benchmarks to represent standard units.

Example

The width of my little finger is almost equal to the length of a centimetre.

While any object can be used as a concrete benchmark, teachers need to ensure that it is used appropriately. The table below outlines some concrete benchmarks, their benefits, and some points to consider before suggesting or accepting their use.

Benchmarks	Benefit	Consideration
Body parts (for example, hand, foot)	They are available to all students at all times.	They are not always ideal concrete benchmarks because of the variation in measurement resulting from the growth of students.
Manipulatives (for example, linking cubes, paperclips)	It is easily available in large quantities and at a reasonable cost.	It should not be the only concrete benchmark used. Since it is commonly used to measure several attributes (for example, length, area, capacity), it is important to indicate which part of the object is being used as a benchmark (for example, the length of the base of a cube). It does not refer to a personal pattern or a significant experience.
Personal items (for example, figurine, stuffed animal, toy car, sneaker)	They are meaningful to students.	They increase the likelihood that students will use them comfortably and make connections to standard units. They encourage the creation of a set of mental images that will serve as personal benchmarks.

At the second level, students replace concrete benchmarks with mental images that they use as a reference to estimate a measurement (for example, using the mental image of the width of the little finger to estimate a length in centimetres).

Example

At this level, students may perceive each unit as a particular object, without fully understanding its meaning within a measurement system.

For example, the student perceives that the thickness of the book is 4 centimetres, but does not understand that this is equivalent to 0.04 metres. Repeated use of mental images of concrete benchmarks promotes understanding of the meaning and size of various standard units and their multiples (for example, centimetre, metre).

At the third level, students integrate benchmarks into a measurement system, including establishing relationships among various standard units of the same attribute (for example, centimetre, metre) and making sense of conversion strategies among these units.

Example

A red door labeled "one meter equals 100 centimeters. A measuring tape, a double arrow that joins the two ends, one meter, a second double arrow equals 100 centimetres.

Benchmark Development

Since reference points are essentially mental images, their development is intimately related to the ability to visualize. Students generally do not have too much difficulty developing appropriate benchmarks for length (for example, they can imagine the length of one side of a small interlocking cube to represent 1 centimetre, or the length of a metre stick to represent 1 metre).

Source: translated from Guide d'enseignement efficace des mathématiques de la maternelle à la 3^e année, Mesure, p. 12-15.

Skill: Estimating Lengths

It is important for students to develop benchmarks before exploring estimation.

Adults, like students, must approximate quantities in a variety of everyday situations; that is, they must estimate (for example, estimate the number of paperclips needed to measure the width of the table). In measurement, estimating is a process based on visual information and prior experience that allows one to make judgments about the approximate size of an attribute (for example, length, time) without resorting to a measurement strategy.

According to Van de Walle and Lovin (2008), it is important to make room for estimation in measurement activities because estimation:

focuses on the attribute to be measured and knowledge of procedures (for example, to estimate the width of a table using straws, first think about what width [length] means and then visualize a way to use straws as a unit of area);
promotes intrinsic motivation (for example, students want to check how accurate their estimate is);
allows one to become familiar with standard units (for example, to estimate the height of the gym in metres benchmarks for one metre are needed).

In the primary grades, students make estimates using primarily non-standard and base standard units. Students develop the ability to estimate using their senses or prior knowledge (for example, estimating the time it would take them to run 200 metres by referring to the time it takes them to run 100 metres).

However, because students have had different experiences, they need to do several estimation activities in class with non-standard or standard units to develop a sense of measurement (for example, repeatedly calculating the length of several objects with their little finger to find out what 1 centimetre is).

Therefore, it is important for teachers to plan instruction focused on specific estimation strategies. Van de Walle and Lovin (2008) suggest teaching four estimation strategies. These strategies are presented in the following table.

Strategy	Example
Develop and use benchmarks for important units of measurement Students who have built up a repertoire of benchmarks and use them regularly are more successful and comfortable estimating. Estimating the measurement of the attribute is done by comparing it with a benchmark.	Students use a known quantity such as the length of a straw or the width of their thumb to determine the length of several common objects in the classroom or home.
Breaking the object down into parts In some contexts, it is easier to estimate the size of an object by first estimating the size of smaller, easily identifiable parts. The estimate of the attribute’s measurement is the sum of the size of each of the parts (concept of additivity).	To estimate the height of a tower created by Kindergarten students, Grade 2 students determine that the height of each block in the tower is about 20 centimetres. Assuming that all the blocks are the same size, students can then estimate that the tower is about 120 centimetres high.
Use subdivisions If the object to be measured has no elements that suggest a way to break it down into parts, it can first be divided mentally or concretely into halves, and then one of these halves can be divided again into halves and the process repeated until a section is obtained whose measurement can be estimated.	To estimate the length of a piece of string or ribbon, students can fold it in half repeatedly until they get a relatively small length. They then estimate the length of that section and multiply by the number of times it has been folded.
Iterate concretely or mentally Iteration refers to the act of placing, repeatedly and in an orderly fashion, the same unit of an attribute. The estimate of the measurement of the attribute is the number of times the unit is placed.	To estimate a student's height using a straw as a unit, students can try to visualize how many times a straw can be placed all the way up that person without overlapping or leaving gaps.

When students engage in estimation activities on a regular basis, they realize that there is no single effective method of estimation. Therefore, the teacher should provide frequent estimation activities related to measurable attributes. These activities are most effective when students discuss, justify, and explain how they arrived at their results. Explanations and justifications of the estimates that students make allow the teacher to learn about, and even assess, their understanding of the concepts and procedures in measurement.

Source: translated from Guide d'enseignement efficace des mathématiques de la maternelle à la 3^e année, Mesure, p. 16-20.

For the attribute length, students need to visualize a one-dimensional space, namely, a mental image of a straight or curved line. For example, in a situation where they are asked to determine the perimeter of a given shape, students need to visualize that they are determining the measure of each of the sides that corresponds to the length of the string placed around that shape. Students also need to recognize that, in some situations, the attribute length can be given a different name, for example:

the height of a mountain;
the width of a prism;
the thickness of a cake;
the height of a person;
the depth of a lake;
the perimeter of a box.

Source: translated from Guide d'enseignement efficace des mathématiques de la maternelle à la 3^e année, Mesure, p. 21

Knowledge: Inverse Relationship (Centimetres and Metres)

The number of units it takes to determine an attribute is inversely proportional to the size of the units. In other words:

the smaller the unit, the greater the count;
the larger the unit, the smaller the count.

Source: translated from Guide d’enseignement efficace des mathématiques, de la maternelle à la 3^e année, Mesure, p. 61.

”How many metres can you place end to end to measure the length of a classroom wall? If we measure the length of the same wall in your classroom in centimetres, will there be more centimetres or metres? Explain your answer.“

Two one-meter rulers are placed end to end.

(A metre is a larger unit than a centimetre, a metre contains 100 centimetres, so less is needed to measure the length of the class. A centimetre is a smaller unit than a metre, so more is needed to measure the length of the class, so the length of the class is 8 metres or 800 centimetres.)

Source: translated from Fiche de la maternelle à la 3e année Attribut longueur, p. 4.

Knowledge: Benchmarks

In measurement, benchmarks are mental images that represent non-standard or standard quantities or units according to a given or personal referent.

Source: translated from Guide d’enseignement efficace des mathématiques, de la maternelle à la 3^e année, Mesure, p. 12.