E1.4 Plot and read coordinates in the first quadrant of a Cartesian plane using various scales, and describe the translations that move a point from one coordinate to another.
Skill: Locating Coordinates in the First Quadrant of a Cartesian Plane Using Various Scales
To locate a point or coordinate in the first quadrant of a Cartesian plane, for example A (2, 4), move 2 units to the right from the origin, then 4 units up.
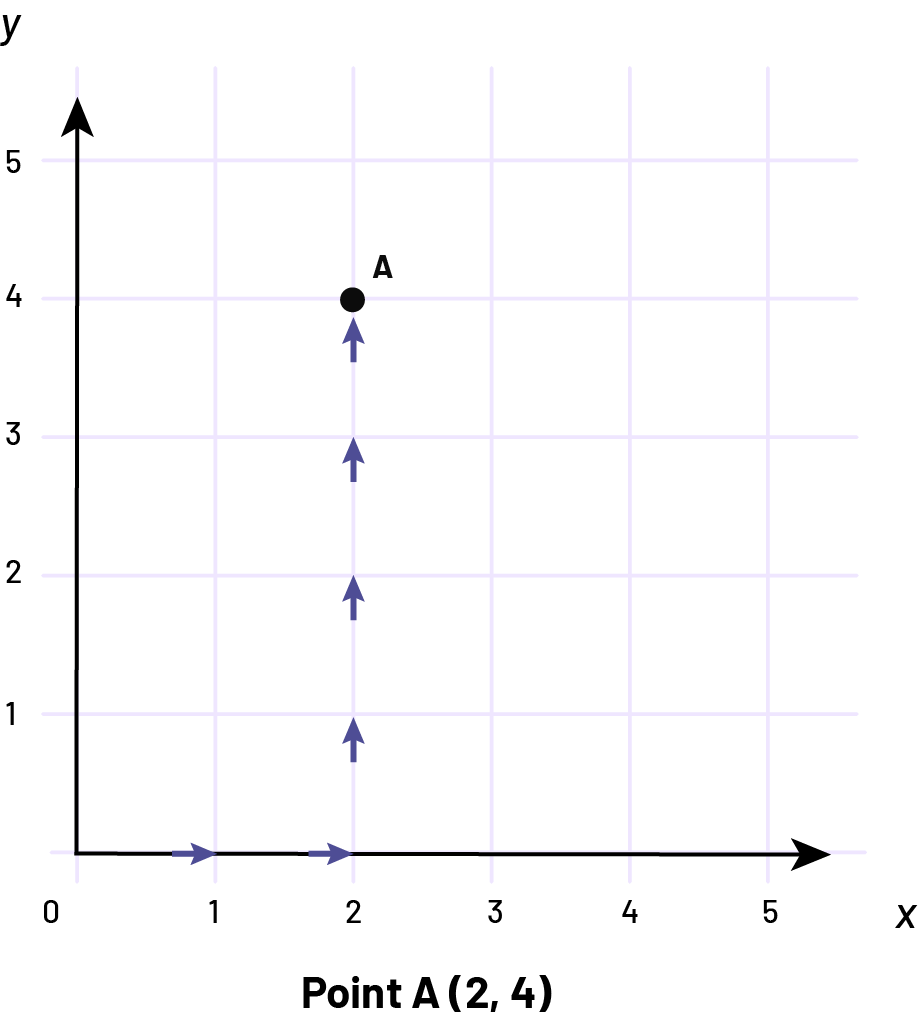image A Cartesian plane quadrant with five columns and five rows. The columns are numbered on the horizontal axis, "x", and the rows on the vertical axis, "y". Horizontal darts start at "y" one, and turn upward from "x" two to point "a" at the intersection of "x" two and "y" four. Below the image is written: point "a" (opening parenthesis), two, four, (closing parenthesis).
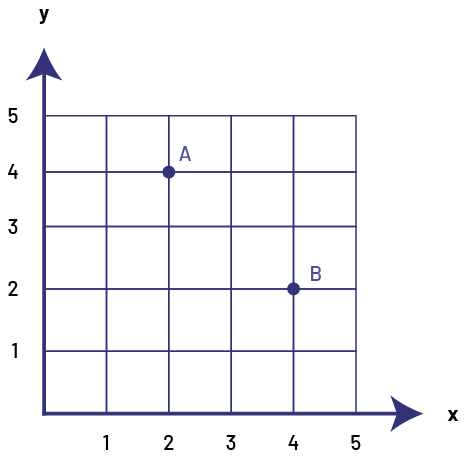
Students should be supported to recognize the importance of the order in which numbers are written in a Cartesian coordinate. To do this, simply ask them to locate, for example, points A (2, 4) and B (4, 2). They will quickly realize that these points describe different positions.
While using the Cartesian plane, students may experience another conceptual difficulty that is linked to the use of the scale on the graduated axes. The difficulty arises when students must locate a point in the Cartesian plane whose coordinates do not correspond to a vertical or horizontal line or to a number on the axes. For example, in a graph where the axes are scaled 1:2, the even numbers are located along the axes to identify the corresponding horizontal and vertical lines. However, the lines corresponding to the odd numbers are not drawn. Students may then believe that a point such as (7, 5), which has odd coordinates, cannot be located in the Cartesian plane, since they do not see any odd numbers on the axes. In Grade 5, students should understand that it is possible to locate this point by mentally visualizing the horizontal and vertical lines between those on the grid of the Cartesian plane.
Examples
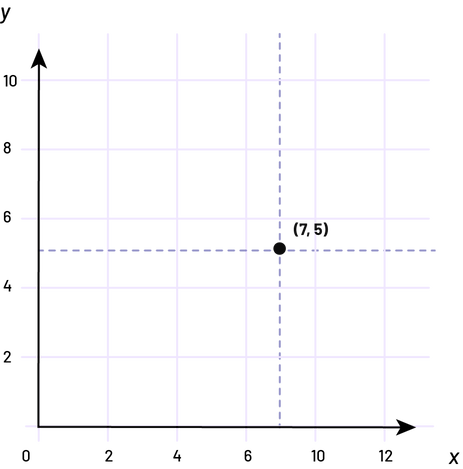image A Cartesian plane quadrant with 12 columns and ten rows. The columns are numbered in increments of two on the horizontal axis, "x", and the rows on the vertical axis, "y". There is a point at the intersection of "x" seven and "y" five. Next to the point is written: (open parenthesis), seven, five, (closie parenthesis).
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Géométrie et sens de l'espace, Fascicule 2, p. 25-26.
image A Cartesian plane quadrant with 60 columns and 60 rows. The columns are numbered in increments of ten on the horizontal axis, i.e. "x", and the rows on the vertical axis, i.e. "y". There is a point at the intersection "x" 45 and "y" 35. Next to the point is written: (open parenthesis), 45, 35, (close parenthesis)
Skill: Reading Coordinates in the First Quadrant of a Cartesian Plane
To read coordinates in the first quadrant of a Cartesian plane, begin at the point and follow the vertical line down to the x-axis. This is the x-coordinate. Do the same again but follow the horizontal line to the y-coordinate. Students need to understand that the Cartesian coordinates, such as (2, 4), define points of intersection of the lines on the grid, and not a square within it.
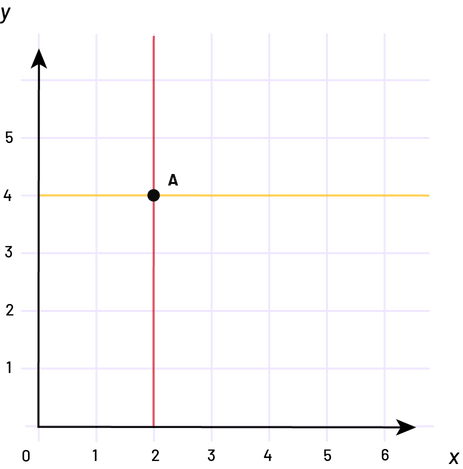image A Cartesian plane quadrant with six columns and five rows. The columns are numbered on the horizontal axis, "x", and the rows on the vertical axis, "y". There is a point "a" at the intersection of "x" two and "y" four. The lines "x" two and "y" four are colored.
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Géométrie et sens de l'espace, Fascicule 2, p. 25-26.
Skill: Describing Movements from One Coordinate to Another Using Translations
In the Cartesian plane, a translation involves distance and direction. Every point on the original shape “slides” the same distance and direction to create a translated image. This combination of distance and direction is called the translation vector.
Source: The Ontario Curriculum. Mathematics, Grades 1-8, Ontario Ministry of Education, 2020.
To describe a horizontal or vertical translation, students use words, letters, or symbols (for example, a translation of six units to the right can be symbolically represented by 6R or 6→). To describe an oblique (diagonal) translation, both the horizontal and vertical movements must be indicated. For example, a translation of six units to the right and two units down is symbolically represented by 6R and 2D or 6→ and 2↓. The order of the symbols does not matter; however, it is best to get students used to always describing the translation by indicating the horizontal movement first and then the vertical movement.
In the junior grades, students determine horizontal, vertical, or oblique (diagonal) translations defined by an arrow. The arrow is usually placed outside the shape. The direction of the arrow corresponds to the direction of the translation and its length corresponds to the magnitude of the movement. To determine the translation, students must determine the magnitude of the horizontal and vertical movements represented by the arrow.
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Géométrie et sens de l'espace, Fascicule 2, p. 28-29.
Knowledge: First Quadrant of a Cartesian Plane
The x and y axes divide the Cartesian plane into four regions called quadrants. In Grade 5 students use the quadrant at the top right of the Cartesian plane. This quadrant is called the first quadrant.
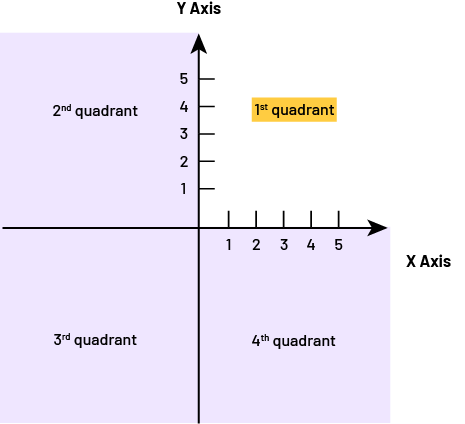
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Géométrie et sens de l'espace, Fascicule 2, p. 24.
Knowledge: Coordinates
The Cartesian coordinate system is used to locate a point on a plane. The coordinates are written in parentheses and are separated by a comma as follows: point A (2, 4). By convention, the first number, called the abscissa, indicates the horizontal position of the point with respect to the origin and the second number, called the ordinate, indicates the vertical position of the point with respect to the origin. Note that grade 5 students are not required to use the vocabulary abscissa and ordinate.
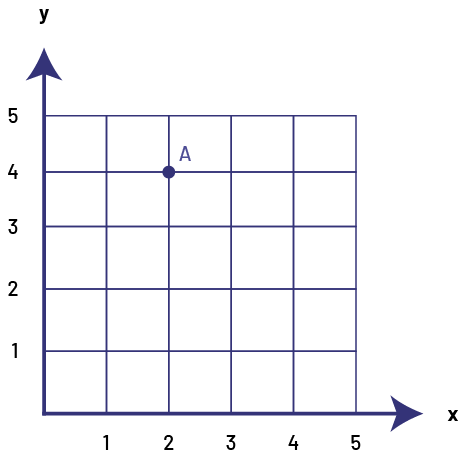
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Géométrie et sens de l'espace, Fascicule 2, p. 25.
Knowledge: Translation
A translation is defined by its size and direction (represented symbolically by coordinates or by an arrow). It represents a linear, horizontal, vertical or oblique (diagonal) movement. The initial shape and the image are congruent. The distance is constant between each point of the initial shape and each corresponding point of the image. The orientation of the image is the same as the orientation of the initial shape.
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Géométrie et sens de l'espace, Fascicule 2, p. 36.
Knowledge: Horizontal Axis
Two perpendicular axes are used to define the Cartesian plane. The horizontal axis is identified by an x and is called the x-axis.
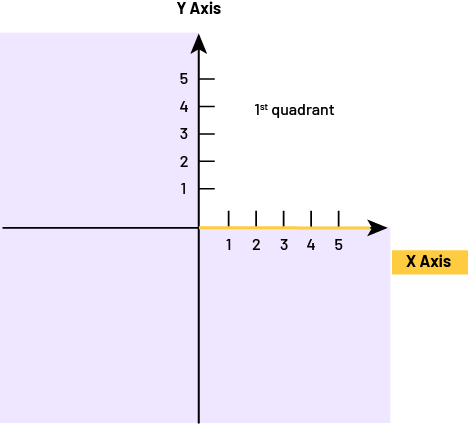
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Géométrie et sens de l'espace, Fascicule 2, p. 24.
Knowledge: Vertical Axis
Two perpendicular axes are used to define the Cartesian plane. The vertical axis is identified by a y and is called the y-axis.
" class="img-fluid">
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Géométrie et sens de l'espace, Fascicule 2, p. 24.
Knowledge: The Origin
The point where the x (horizontal) and the y (vertical) axes meet, which serves as a reference point, is the origin.
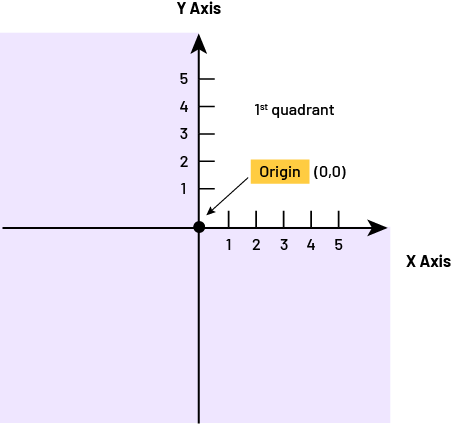
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Géométrie et sens de l'espace, Fascicule 2, p. 24.