La vue d'ensemble

At a Glance...

The Guides for Effective Instruction in Mathematics Revised

FrançaisEnglish

E2.3 Compare angles and determine their relative size by matching them and by measuring them using appropriate non-standard units.

Skill: Overlapping Angles to Compare and Determine Their Respective Sizes

The third step in the act of measuring is to determine the measurement of an attribute of an object, that is, to give an order of magnitude or size to the attribute by quantifying it in terms of a unit.

Compare and Order

Comparing and ordering involves comparing two objects based on the same attribute. To give an idea of the length of their pencil, for example, a student can compare the length of the pencil with the length of a pen and conclude: “My pencil is a little longer than this pen. This strategy does not, strictly speaking, quantify the measurement of an attribute of an object; it simply makes it possible to fix an order of magnitude or size of this attribute by establishing that it is larger or smaller than the same attribute of another known object. Everyone uses this strategy in many situations where they feel that it is not really necessary to quantify the measurement. To ensure that a wrapping paper is long enough to wrap a box, for example, simply compare the perimeter of the box to the length of the paper by successively overlapping four of the sides of the box on the paper.

The measurement of an attribute of two objects is compared, either by direct comparison or by indirect comparison.

From an early age, children compare the measurement of an attribute of two objects by direct comparison (for example, the length of two chocolate bars, their height relative to another child). They then communicate the result descriptively rather than quantitatively (for example, "This chocolate bar is longer than that one.", "I am shorter than you.") Direct comparison is usually done either by placing one object on top of another or by placing the two objects side by side or back to back.

Example

A hexagon, half of which is covered by four parallelograms. Next to this image is a magnifying glass that magnifies an angle of a smaller hexagon.

Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Mesure, p. 89-90.

Skill: Measuring Angles Using Appropriate Non-Standard Units to Compare and Determine Their Respective Sizes

The second step in the act of measuring is to select an appropriate non-standard or standard unit to measure some attribute of an object. To do this, it is important to choose a unit that reflects the attribute to be measured and is appropriate for the situation. In addition, it is generally best to use a single unit.

Steps in the Act of Measuring

  1. determine the attribute to be measured;
  2. choose the unit;
  3. determine the measurement;
  4. communicate the result.

When first exploring an attribute of an object, it is best for teachers to encourage students to choose a non-standard unit, so that they can better focus on the meaning of the attribute and  how it might be measured. Then, they can point out the limitations of the non-standard  unit and the advantages of using a standard unit.

Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Mesure, p. 86.

The third step in the act of measuring is to determine the measure of an attribute by quantifying it in terms of a unit.

Steps in the Act of Measuring

  1. determine the attribute to be measured;
  2. choose the unit;
  3. determine the measurement;
  4. communicate the result.

Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Mesure, p. 89.

Since it is difficult to move and compare angles directly (by overlapping and matching them), it is common to compare them indirectly by using a third angle to make the comparison.

  • If the third angle can be adjusted and transported, it can be made to match the first angle and then be moved to the second angle to make the comparison directly. This involves the property of transitivity (if A equals C, and C is greater than B, then A is also greater than B).

Source: The Ontario Curriculum. Mathematics, Grades 1-8 Ontario Ministry of Education, 2020.

Fundamental Concept : Transitivity

The student who understands this concept can establish a relationship of equality or inequality between the magnitude of three angles by comparing the magnitude of one angle with the magnitude of the other two.

Example

How can we determine, without moving the two tables below, if the hexagon-shaped table can be placed in the opening of the grey table?

A large sheet of paper can be used to trace the size of the opening in the grey table, and then superimposed on the corners of the hexagon-shaped tabletop. If the size of the traced angle is equal to the size of any corner of the hexagon-shaped table, the hexagon-shaped table can fit snuggly against the grey table.

An irregular shape with seven sides and a hexagon.

Source: translated from Fiche de la 4e à la 6e année, Attribut angle.

  • If the third angle is a smaller but fixed angle, it can operate as a unit that is iterated to produce a count. Copies of the third angle are fitted into the other two angles to produce a count. The unit count is compared to determine which angle is greater and how much greater.

Source: The Ontario Curriculum. Mathematics, Grades 1-8 Ontario Ministry of Education, 2020.

Fundamental Concept : Iteration

The student who understands this concept is aware that the measure of an angle is equal to the sum of the measures of each of its parts.

Example

Can you determine the measurement of the angle below using a single beige rhombus?

Simply iterate the rhombus, without gaps or overlaps, to fill the opening formed by the rays. The angle measurement is the number of times the rhombus has been used.

An angle formed by two arrows. A parallelogram is placed in the angle.

Source: translated from Fiche de la 4e à la 6e année, Attribut angle.

Fundamental Concept: Additivity

The student who understands this concept is aware that the measurement of an angle is equal to the sum of the measurement of each of its parts.

Example

Is it possible to create a 360° angle using four pentablocks?

Yes, it is possible, as shown by the few examples below. The sum of the measures of the four angles that meet is equal to 360°.

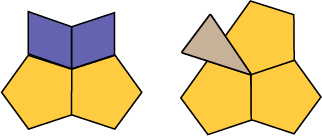
There are three illustrations. The first one is made of two hexagons and the congruent parallelogram. The second illustration is of a parallelogram. The third illustration is of three parallelograms and a triangle.

Source: translated from Fiche de la 4e à la 6e année, Attribut angle.

Knowledge: Angles

An angle is the magnitude of an "opening".

An angle can be determined by:

  • two rays having a common endpoint;
  • two intersecting half-planes;
  • a rotation around a point.

Examples

Angle formed by two rays sharing a common endpoint.

There are two corners. The first one is formed by two arrows, and a third curved arrow marks the inner angle. The second angle is formed by two arrows, and a third arrow marks the outer angel.

Angle formed by two intersecting half-planes.

There is an open book. On one right side of the book there is a curved arrow that joins the other left side.

Angle formed by a rotation around a point.

A clock, with hands pointing to 12 and seven. There is a curved arrow from 12 to seven.

Fundamental Concept: Conservation

The student who understands this concept becomes aware that the size of an angle remains the same whether the angle is moved, transformed, or decomposed.

The student should also understand that the size of an angle is preserved even if the line segments that determine the angle are lengthened or shortened.

Source: translated from Fiche de la 4e à la 6e année, Attribut angle.