E1.2 Identify and construct congruent triangles, rectangles, and parallelograms.
Activity 1: Construction of Congruent Rectangles and Parallelograms
Ask students to find objects that are shaped like rectangles and other types of parallelograms. Ask them to draw a congruent shape without tracing the object.
Ask them questions such as:
- What tools do you need to construct a shape congruent to this one? How will you use them?
- Do you use the tools the same way for rectangles and parallelograms? Explain.
- What properties must the object and the shape share in order to be congruent?
- How can you verify that your shape is congruent with the object you selected?
- What other strategies can you use to construct a congruent shape?
Activity 2: Constructing Congruent Triangles
- As part of a schoolyard redesign project, the principal asks your class to create a garden area that contains three garden boxes, as shown below. The bases of the garden boxes must have different triangular shapes. You must draw sketches of the three bases.

The principal presents the class with a sketch of the triangular shape they would like for one of the bins. Construct a triangle that is congruent to the one below.

- Here is the first floor plan of a modern house:
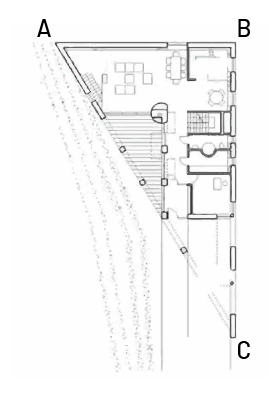
The measurements are as follows:\(\angle ABC\) measures \(90^{\circ}\), \(\angle BAC\) measures \(60^{\circ}\) and \(\angle BCA\) measures \(30^{\circ}\). The segment AB measures 7.8 cm.
- Construct a triangle congruent with the shape of this plan and indicate the measurements and angles you drew.
- What kind of triangle does this modern house represent? Explain your reasoning.
Source: translated from En avant, les maths!, 5e année, ML, Sens de l'espace, p. 14-16.
