La vue d'ensemble

At a Glance...

The Guides for Effective Instruction in Mathematics Revised

FrançaisEnglish

E2.5 Show the relationships between the radius, diameter, and area of a circle, and use these relationships to explain the formula for measuring the area of a circle and to solve related problems.

Activity 1: Develop the Formula for the Area of a Circle

  1. Trace the outline of a paper plate with a felt-tip pen.
  2. Fold the paper plate in two equal parts. The fold represents the diameter of the circle.
  3. Fold the paper plate in two equal parts a second time. The fold represents the radius of the circle.
  4. Calculate the circumference of the paper plate. Explain your strategy.

Area of a Circle

  1. Fold the paper plate in half a third time. Continue to fold the plate in half until you can no longer do it.
  2. Cut out the paper plate on the folds. The cut-out pieces represent the sectors of the circle.
  3. On a large sheet of paper, draw a line.
  4. Place half of the cut-out sectors on the sheet, aligning the curved outline of the sectors (outline of the plate) with the line you just drew.
  5. Place the other half of the cut-out sectors on the sheet, inserting them between the sectors already placed so that the spokes are aligned (side by side) while limiting the space between them.
  6. Glue the sectors of the circle onto the sheet.
  7. Calculate the area of the paper plate. Explain your strategy.
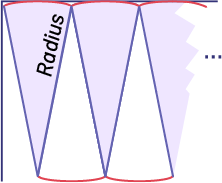
The representation of a paper plate that has been folded, and cut, so that the department can be identified.

What do you notice? What shape do the sectors of the circle glued to the paper remind you of? How could you calculate the area of this shape? How can you relate the area of this shape to the area of the circle?

Source: translated from En avant, les maths!, 7e année, ML, Sens de l’espace, p. 14.

Activity 2: Area of the Circle According to Its Diameter

Determine, to the nearest tenth, the area of this circle. Describe your process and your thinking to arrive at your answer.

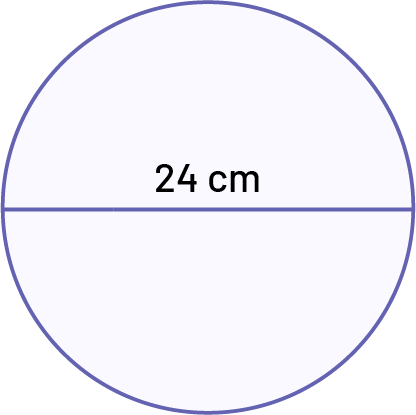
A disc 24 centimeters in diameter.

Source: adapted and translated from En avant, les maths!, 7e année, ML, Sens de l’espace, p. 15.

Activity 3: Area of the Circle According to Its Radius

Determine, to the nearest tenth, the area of this circle. Describe your process and your thinking to arrive at your answer.

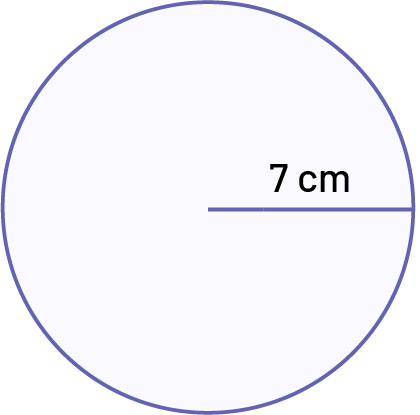
A disc 7 centimeters in radius.

Source: adapted and translated from En avant, les maths!, 7e année, ML, Sens de l’espace, p. 16.

Activity 4: Problems Related to the Area of a Circle

  1. The table below shows the sizes of pizza and the number of pieces of each in the vast majority of pizzerias.

Size

Diameter (cm)

Number of Pieces

Small

28

4

Medium

33

6

Large

38

8

Very large

43

10
    1. Calculate the area of each of the pizzas.
    2. Calculate the area of a piece of pizza of each size.
    3. Rank the size of the pizza pieces in descending order.
  1. You aim for the bull's eye which has a diameter of 1 cm. How many times smaller is its area than the area of the outermost circle if it has a diameter of 20 cm? Show all your calculations.
A circular target.