C1.2 Créer des suites à l’aide de mouvements, de sons, d’objets, de formes géométriques, de lettres et de nombres, et représenter les suites de différentes façons.
Habileté : représenter les suites de différentes façons
Suites à motif répété
L’utilisation de représentations multiples d’une même suite pour communiquer sa compréhension est une composante essentielle du développement de la pensée algébrique. Les suites à motif répété peuvent être représentées à l’aide de matériel concret ou semi-concret, de symboles ou de descriptions orales.
Exemples de modes de représentation
|
Modes de représentation |
Exemples |
|
Matériel concret |
Suite A : Suite faite avec le corps (par exemple, sons, mouvements, positions) Suite B : Suite faite avec des objets (par exemple, un collier) |
|
Matériel semi-concret |
Suite illustrée 
|
|
Descriptions orales |
Suite A : « C’est une suite parce que les positions debout bras tendus et accroupi se répètent toujours dans le même ordre. » Suite B : « Le collier fait une suite parce que les quatre couleurs se répètent toujours de la même façon. » Suite C : « C’est une suite parce que le motif, soit un camion d’incendie suivi d’un pompier, se répète toujours dans cet ordre. » |
|
Symboles |
Suite A : La structure de la suite est AB. Suite B : La structure de la suite est ABCD. Suite C : La structure de la suite est AB. |
Les élèves peuvent montrer leur compréhension des concepts de régularité et de relations et développer davantage leurs habiletés à reconnaître, à décrire et à prolonger une suite en changeant la représentation d’une suite sans en modifier la règle.
Le changement peut se faire d’un mode à un autre; par exemple, une suite non numérique telle que celle illustrée ci-dessous peut être représentée avec les mouvements « tape, saute, saute » ou avec de petits animaux en plastique « chat, chien, chien ».

Le changement peut aussi se faire à l’intérieur d’un même mode de représentation.
Exemple


En représentant une suite à l’aide de symboles, on peut déterminer clairement sa structure. Pour ce faire, des lettres sont utilisées selon l’ordre alphabétique. Chaque nouvelle lettre représente un élément différent dans le motif. Dans les suites présentées ci-dessus, la structure est AABB.
Souvent, plusieurs représentations d’une même suite constituent une bonne justification mathématique, puisque chacune d’elles contribue à la compréhension des idées présentées. L’habileté à créer, à interpréter et à représenter de plusieurs façons ses idées est un outil puissant.
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, p. 34-36.
Suites à motif croissant
Les suites à motif croissant, tout comme les suites à motif répété, peuvent être représentées à l’aide de matériel concret ou semi-concret, de symboles ou de descriptions orales.
Exemples de modes de représentation
|
Modes de représentation |
Exemples |
|
Matériel concret |
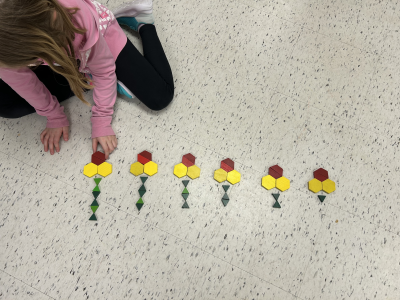 |
|
Matériel semi-concret |
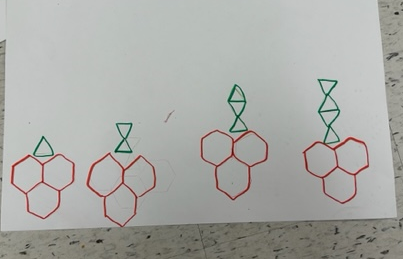 |
|
Description orale |
« Un tronc est toujours ajouté au tronc de l’arbre précédent. » |
|
Symboles |
Dans le dessin ci-dessus, la règle de régularité de la suite de figures peut être représentée symboliquement par le signe d’addition et le nombre (+ 1). |
Le personnel enseignant doit donner aux élèves l’occasion d’explorer et de créer diverses représentations d’une même suite. À titre d’exemple, il peut leur demander d’échanger au sujet de leur représentation et de reproduire la suite à l’aide de matériel concret ou semi-concret, et vice-versa. Il est important de s’attarder à la relation entre les deux représentations pour que l’accent demeure sur le raisonnement et non sur le calcul numérique.
Suites numériques
L’acquisition des concepts relatifs aux suites numériques est un préalable à l’étude des concepts algébriques plus abstraits. L’exploration de diverses représentations de suites numériques facilite l’entrée dans le monde algébrique.
Au cycle primaire, certaines représentations facilitent le développement des habiletés en résolution de problèmes, en raisonnement et en communication. Les représentations des suites numériques explorées au cycle primaire sont réalisées à l’aide de matériel concret ou semi-concret (tableau de nombres, droite numérique, grille de nombres), de symboles et de descriptions orales.
Exemples de modes de représentation
|
Modes de représentation |
Exemples |
|
Matériel concret |
  |
|
Matériel semi-concret |
 |
|
Matériel semi-concret |

|
|
Descriptions orales |
« La suite numérique est : six légumes la 1re semaine, 12 légumes la
2e semaine, 18 légumes la 3e semaine, 24 légumes la 4e semaine et
30 légumes |
|
Symboles |
Dans l’exemple précédent, la règle de régularité dans la suite numérique est représentée par le signe + et le nombre 6, soit + 6. |
Les représentations de suites numériques se font à l’aide de divers matériels concrets et semi-concrets. Dans ce qui suit, les types de matériel de manipulation énumérés ci-dessous seront utilisés comme modèles pour approfondir la compréhension des suites numériques :
- le tableau de nombres;
- la grille de nombres;
- la droite numérique;
- la calculatrice.
Le tableau de nombres
Les régularités dans un tableau de nombres sont multiples, de même que la disposition des suites; par exemple, dans un tableau de 100 tel que celui illustré ci-dessous, une suite avec la règle de régularité + 2 sera disposée en rangée (61, 63, 65…); si la règle de régularité est + 10, la suite sera disposée en colonne (7, 17, 27…); si la règle de régularité est + 11, elle sera disposée en droite oblique (1, 12, 23…). Dans un tableau de nombres, les cartes de nombre peuvent facilement être déplacées, tournées ou enlevées pour créer des suites.

La grille de nombres
Voici quelques stratégies possibles pour explorer les suites numériques avec une grille de nombres de 50 :
- Utiliser des jetons de bingo pour identifier une suite sur une grille de 50. L’utilisation de jetons aide les élèves à faire des modifications sans devoir effacer.
Exemple 1
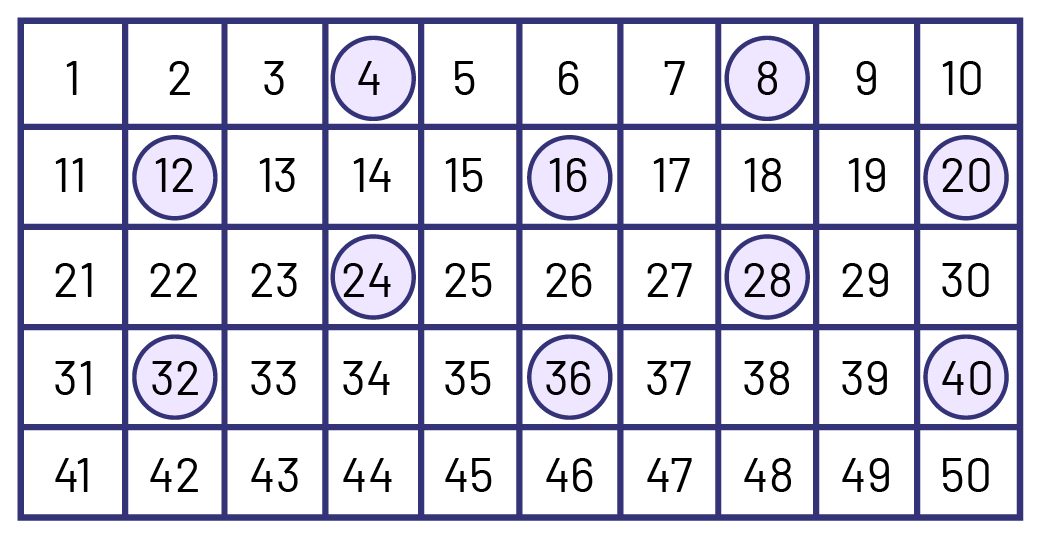
Suite: 4, 8, 12, 16, 20, 24, 28, 32, 36, 40
Règle de régularité : + 4
-
Utiliser un pochoir et le déplacer sur la grille pour repérer une suite numérique. Déterminer la règle de régularité dans cette suite et la prolonger.
Exemple 2
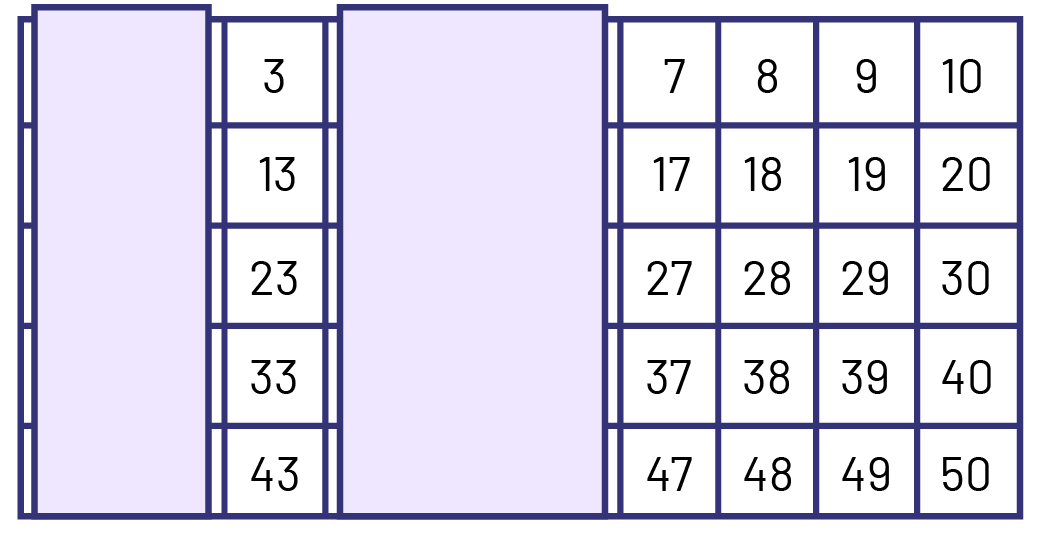
Suite : 3, 13, 23, 33, 43
Règle de régularité : + 10
- Présenter des sections de la grille et repérer une suite numérique. Déterminer la règle de régularité dans cette suite.
Exemple 3
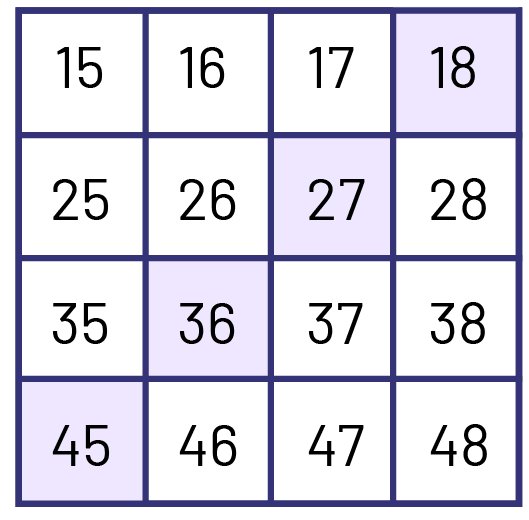
Suite : 18, 27, 36, 45
Règle de régularité : + 9
Au cours de l’exploration de suites numériques avec une grille de 50, poser aux élèves des questions afin de développer leur habileté à les représenter.
- Que remarquez-vous au sujet des nombres qui font partie de la suite?
- Quel changement y a-t-il d’un nombre à l’autre dans chaque rangée ou chaque colonne? (Ils augmentent ou diminuent de 1 ou de 10.)
- Si l’on déplace le pochoir et que le premier nombre est 5, le nombre 46 apparaîtra-t-il? Expliquez votre réponse.
La droite numérique

Utilisée comme modèle pour faire découvrir les règles de régularité dans des suites, la droite numérique aide à représenter une variété de régularités. La représentation de la droite numérique peut être concrète ou semi-concrète.
« Les modèles mathématiques sont des cartes mentales de relations qui peuvent être utilisées comme outil pour résoudre des problèmes; par exemple, lorsque des mathématiciens pensent à un nombre, elles et ils peuvent avoir une droite numérique en tête. Elles et ils visualisent les nombres, les uns par rapport aux autres, sur la droite et se représentent les déplacements sur la droite. » [traduction libre] (Fosnot et Dolk, 2001, p. 77)
Voici quelques stratégies possibles pour explorer les suites numériques avec la droite numérique :
- Au départ, utiliser une droite numérique plastifiée sur laquelle les élèves peuvent effectuer des bonds sur les nombres, à intervalles réguliers, en sautant ou en utilisant un objet quelconque.
- À l’aide d’une droite numérique tracée sur une grande feuille de papier, les élèves encerclent les termes de la suite et indiquent, à l’aide d’une flèche, la règle de régularité dans la suite.
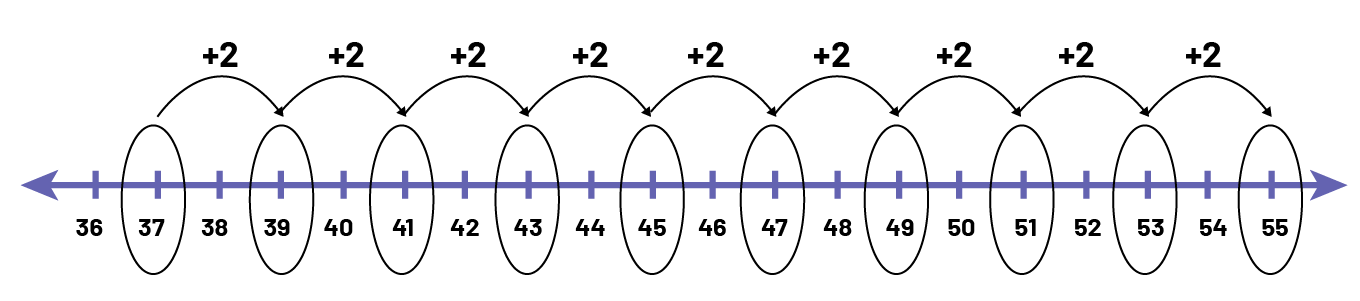
Au cours de l’exploration de suites numériques à l’aide d’une droite numérique, poser aux élèves des questions telles que :
- Le nombre 48 ferait-il partie de la suite si l’on prolongeait la droite?
- Que remarquez-vous en ce qui a trait aux nombres encerclés sur la droite numérique?
- Quelle est la règle de régularité dans la suite? Comment est-elle indiquée?
- Si la suite débutait par le nombre 1, qu’est-ce qui serait pareil? différent?
- Si la suite débutait par le nombre 2, qu’est-ce qui serait pareil? différent?
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, p. 50-59.
Habileté : créer diverses suites
Avant de créer des suites, les élèves doivent d’abord reconnaître, comparer, décrire, changer la représentation et prolonger une grande variété de suites.
Les élèves montrent leur compréhension du concept de régularité en créant une suite et en l’expliquant.
Au départ, l’utilisation du matériel de manipulation est indispensable pour représenter les suites, car, en en créant, les élèves peuvent facilement changer un élément du motif et vérifier la règle. Lorsque les élèves la dessinent sur du papier, elles et ils se concentrent sur le dessin à reproduire plutôt que d’examiner toute la suite et de réfléchir à la nature de la règle.
Au début, le personnel enseignant fait travailler les élèves en petits groupes afin de favoriser l’échange d’idées. Il peut leur fournir les attributs et la structure de la suite, ainsi que le matériel requis pour la créer.
Le personnel enseignant peut ensuite demander aux élèves de créer leur propre suite et de l’échanger avec celle d’une ou d’un partenaire. Les élèves peuvent alors construire une représentation différente de la suite reçue, décrire sa structure, la prolonger ou en produire une totalement différente aux fins de comparaison. Il faut cependant limiter le nombre d’éléments dans le motif, car certaines et certains élèves en utilisent trop, ce qui rend difficile l’identification de la structure de la suite.
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, p. 39-40.
Le personnel enseignant qui veut amener les élèves à créer des suites numériques peut suivre la même démarche que celle suggérée pour les suites non numériques.
Voici quelques exemples d’activités visant à créer des suites numériques :
- Demander aux élèves de créer des suites ayant une règle relative aux intervalles 1, 2, 5 ou 10 et de les comparer.
- Demander aux élèves de créer une suite numérique qui débute par 12 et dont la règle de régularité d’addition est de + 2.

Note : Il est important que les élèves laissent des traces de leur démarche pour s’y référer au cours de l’échange mathématique; par exemple, elles et ils peuvent :
- encercler les termes de chaque suite;
- dessiner une flèche au-dessus de chaque bond pour indiquer l’intervalle;
- représenter symboliquement la règle de régularité à l’aide du signe +, comme dans l'exemple suivant.
Solution possible

Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, p. 63-65.
