C1.3 Déterminer et utiliser les règles pour prolonger des suites, faire et justifier des prédictions, et trouver des termes manquants dans des suites représentées à l’aide de formes géométriques et de nombres (suites numériques et non numériques).
Habileté : déterminer et utiliser les règles pour prolonger des suites
Analyse du changement
Les élèves vivent dans un monde en changement. Comprendre que le changement fait partie de la vie et que la majorité des choses changent avec le temps (par exemple, chaque année pendant la période de croissance, la taille croît, le poids augmente, les pieds allongent) est une dernière composante du développement de la pensée algébrique. Les changements observés peuvent être décrits de façon qualitative (par exemple, j’ai grandi cette année, mes cheveux sont plus longs, le seau s’est rempli d’eau rapidement pendant l’orage, il fait plus froid cet après-midi que ce matin) et de façon quantitative (par exemple, j’ai grandi de 2 cm cette année, le seau s’est rempli de 50 ml d’eau en 30 minutes, la température a chuté de 6 °C en 3 heures). Les élèves doivent apprendre à observer et à comprendre les changements dans les régularités.
Le changement et les régularités sont deux concepts qui ne peuvent être dissociés dans l’étude des suites. Les élèves
réalisent que le changement d’un terme influe sur le terme suivant. Par la suite, l’observation des changements et des
relations entre ces changements leur permet de prédire d’autres termes de la suite et ainsi de généraliser.
À
titre d’exemple, en observant la suite non numérique à motif répété ci-dessous, les élèves peuvent la prolonger et
trouver la régularité, ainsi que décrire la règle de régularité en expliquant la répétition du motif soleil, soleil,
cœur.
Suite non numérique à motif répété
En examinant le changement qui se produit d’un rang à l’autre, les élèves observent une règle de régularité qui leur permet de prédire les figures aux prochains rangs.
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, p. 21-22.
L’essentiel est de développer le raisonnement algébrique chez les élèves, en les rendant capables de justifier le prolongement d’une suite non numérique ou numérique et d’expliciter les relations qui existent entre les termes de la suite.
Les relations entre les termes
En utilisant diverses représentations et du matériel varié, les élèves explorent le concept de régularité dans des suites non numériques et numériques, et communiquent en leurs propres mots ou par des représentations personnelles, leurs observations et leurs perceptions des relations entre les termes de la suite.
Au cycle primaire, les élèves apprennent à reconnaître les relations qui existent entre les termes d’une suite. En examinant et en explorant des suites, les élèves cernent comment cette information peut être utilisée pour déterminer ce qui doit être ajouté à une suite pour la prolonger. En découvrant les relations, les élèves comprennent que les prochains termes dans la suite ne sont pas choisis aléatoirement. La recherche de règles est, en soi, une importante stratégie de résolution de problèmes.
L’image mentale que se font les élèves des régularités est continuellement redéfinie. Leur représentation est souvent limitée par les exemples qui leur sont présentés ou par leurs expériences personnelles. Il importe donc de leur présenter, pendant des activités, une variété de représentations et de régularités pour faciliter l’intégration du concept. L’essentiel est que les élèves développent le raisonnement algébrique en devenant capables de justifier le prolongement d’une suite non numérique ou numérique et en explicitant les relations qui existent entre les termes de la suite.
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, p. 27.
Suites non numériques
Afin de prolonger une suite, les élèves doivent identifier les éléments du motif et leur ordre. En prolongeant une suite tout en justifiant leur choix, les élèves communiquent leur compréhension de ce qu’est la règle. Par exemple, l’élève peut dire : « Je vais être le voilier parce que, juste avant moi, c’est le ballon, et la suite c’est toujours voilier, ballon, voilier, ballon… qui se répètent. »
À l’aide de leur corps ou du matériel de manipulation, les élèves peuvent explorer le prolongement d’une suite et faire des changements avec plus de facilité, et aussi prolonger une suite construite par d’autres.
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, p. 38.
Suites numériques
Très tôt, les élèves prennent conscience des régularités dans leur environnement, dans la nature, dans les objets qui les entourent. C’est pourquoi il est possible de leur présenter les suites numériques dès la 1re année. Parallèlement, les élèves développent leur sens du nombre, peuvent compter par intervalles et à rebours et, par la suite, s’approprient le concept d’addition en tant que regroupement d’objets. Tous ces concepts ont un lien important avec l’apprentissage des régularités numériques.
L’exploration du système de numération à base dix, synonyme de système décimal, permet aux élèves de découvrir qu’il y a une répétition des chiffres de 0 à 9 en comptant au-delà de 9 (10, 11, 12, 13, 14, 15…). De voir et de justifier cette régularité dans le système décimal améliore leur compréhension du sens du nombre et des regroupements (unités, dizaines, centaines, etc.). Par exemple, en comptant par bonds de 2, à partir de 16, les élèves observent une régularité prévisible dans les nombres (16, 18, 20, 22, 24, 26, 28, 30, 32…). C’est un premier pas vers l’exploration des multiples de 2. Cette compréhension les mène aussi à développer la capacité de compter à partir de tout nombre en utilisant n’importe quel bond.
De même, lorsque les élèves comptent par bonds de 5, cela leur permet de reconnaître rapidement une régularité, c’est-à-dire que le chiffre des unités alterne entre le chiffre 0 et le chiffre 5 (5, 10, 15, 20…). Les élèves peuvent généraliser cette découverte informellement en disant que tout nombre qui est un multiple de 5 va se terminer par le chiffre 5 ou 0.
Il peut être utile pour le personnel enseignant de proposer aux élèves d’identifier les régularités dans une grille de nombres pour les aider à développer leur compréhension conceptuelle du nombre et du système de numération à base dix.
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, p. 49-50.
Habileté : faire et justifier des prédictions
L’utilisation de matériel concret et semi-concret ainsi que d’une variété de représentations et de règles permet aux élèves de faire et de justifier des prédictions proches et lointaines.
Faire une prédiction proche consiste à indiquer ou à représenter à quoi ressembleront les prochains termes d’une suite donnée. La prédiction peut être vérifiée simplement en prolongeant la suite.
Faire une prédiction lointaine consiste à indiquer ou à représenter à quoi ressemblera une suite bien au-delà d’une suite donnée. Des calculs sont souvent nécessaires pour faire une prédiction juste ou pour en vérifier sa vraisemblance.
Source : Curriculum de l’Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l’Éducation de l’Ontario.
Les élèves décrivent mieux une suite en comprenant la relation entre chaque terme de la suite et la position qu’occupe chacun dans la suite. Il leur suffit de numéroter successivement chaque terme de la suite.
Ainsi, les élèves peuvent se référer à certains termes spécifiques de la suite (par exemple, dans la suite ci-dessus, les soleils sont au 3e, au 6e et au 9e rang à partir de la gauche). En analysant la relation entre le rang et le terme, il est facile de prédire les prochains termes dans la suite, sans avoir à la prolonger. Cette analyse permet aux élèves de généraliser (par exemple, un soleil sera au 12e rang, puisqu’il est au 3e rang de chaque motif. Le rang du soleil est toujours un multiple de 3).
Dans la situation-problème « Combien de soleils sont nécessaires pour compléter 10 motifs de cette suite? », les élèves du cycle primaire peuvent discuter informellement, modeler et créer des représentations multiples, les décrire et conclure en identifiant le nombre de soleils nécessaires et en justifiant leur démarche. L’exploration de ce genre de problème permet aux élèves de développer leur pensée algébrique et leur sert de fondement à l’utilisation d’une règle et de variables dans les années d’études à venir.
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, p. 38-39.
Dans les suites non numériques à motif croissant, il existe aussi une relation entre le rang de chaque figure et le nombre d’éléments dans chacune. Cette relation est un concept mathématique très important qui mène à une généralisation plus formelle, soit la formulation de la règle de correspondance.
En analysant attentivement une suite, par exemple, les élèves observent que la figure au 1er rang comprend
deux formes géométriques, que la figure au 2e rang en a trois, que la figure au 3e rang en a
quatre, etc. Leur constatation est qu’il y a toujours une forme géométrique de plus que le rang de la figure. Cette
constatation, soit la règle de correspondance, leur permet de trouver n’importe quel terme de la suite sans avoir à la
prolonger.
Des discussions informelles traitant des relations entre les figures et le nombre d’éléments qui
les composent peuvent se produire en déterminant la règle et en prolongeant la suite.
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, p. 45-46.
Habileté : trouver des termes manquants dans des suites
Dans les suites non numériques et numériques, les élèves doivent déterminer ce qui se trouve à une position prédéterminée (avant, après ou à l’intérieur de la suite). Il leur faut donc déterminer la règle pour être en mesure de cibler la figure ou le nombre manquant.
Exemple
Trouve le 2e terme de la suite à motif croissant suivante.
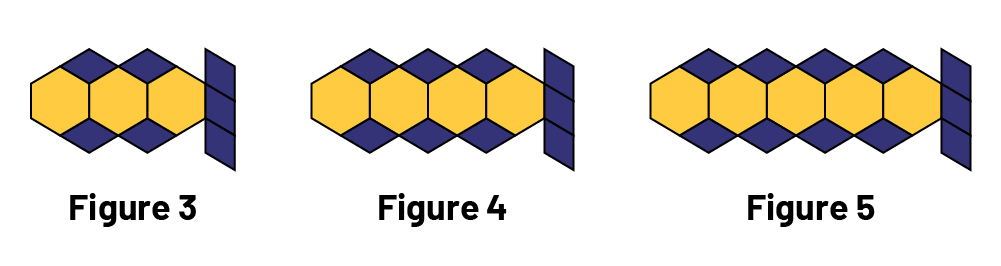
Source : En avant les maths!, 2e année, CM, Algèbre, p. 4.
L’étude des régularités dans une suite numérique peut se poursuivre à l’aide d’une grille de nombres ou d’une droite numérique ayant des nombres manquants. Les élèves doivent d’abord trouver la règle afin de découvrir les nombres manquants, puis expliquer la règle de régularité d’addition ou de soustraction. La calculatrice peut leur être utile pour résoudre ce genre de problèmes.
Exemples
Nombres manquants dans une grille de nombres partielle
Image Un tableau
dont les cases sont ombrées. Le modèle montre les numéros onze et douze avec deux carrés ombrés. La rangée suivante
montre les numéros 21 et 22 et deux carrés ombrés. Dans la troisième rangée, les deux premiers carrés sont ombrés et
les deux derniers carrés représentent les numéros 33 et 34. Enfin, dans la dernière rangée, les deux premiers chiffres
sont révélés. Il s'agit des numéros 41 et 42, et les derniers carrés sont cachés.
Nombres manquants sur une droite numérique ouverte
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, p. 67.
Connaissance : règles
Règle de régularité : Règle qui permet de prolonger une suite en respectant la différence entre les termes (aussi appelé bond constant).
Règle de correspondance : Règle qui permet de prolonger une suite en établissant la relation entre le rang et son terme.
Source : Curriculum de l’Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l’Éducation de l’Ontario.