C1.2 Créer des suites croissantes et des suites décroissantes, à l’aide d’une variété de représentations, y compris des tables de valeurs et des représentations graphiques, et établir des liens entre les différentes représentations.
Activité 1 : les amis de mes amis (représenter une suite)
Présenter la situation ci-dessous aux élèves.
Permettre aux élèves de représenter la situation à l’aide de la stratégie de leur choix.
Exemples
Représenter une situation à l’aide d’une table de valeurs
| Jour | Nombre d’appels |
|---|---|
| 1 | 4 |
| 2 | 16 |
| 3 | 64 |
Représenter une situation à l’aide d’une représentation graphique
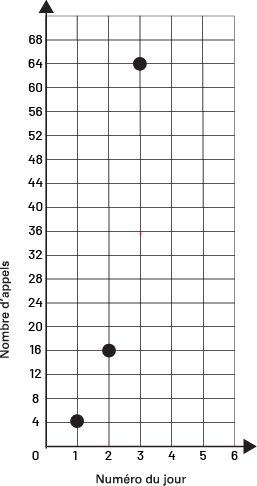
Représenter une situation à l’aide de matériel semi-concret
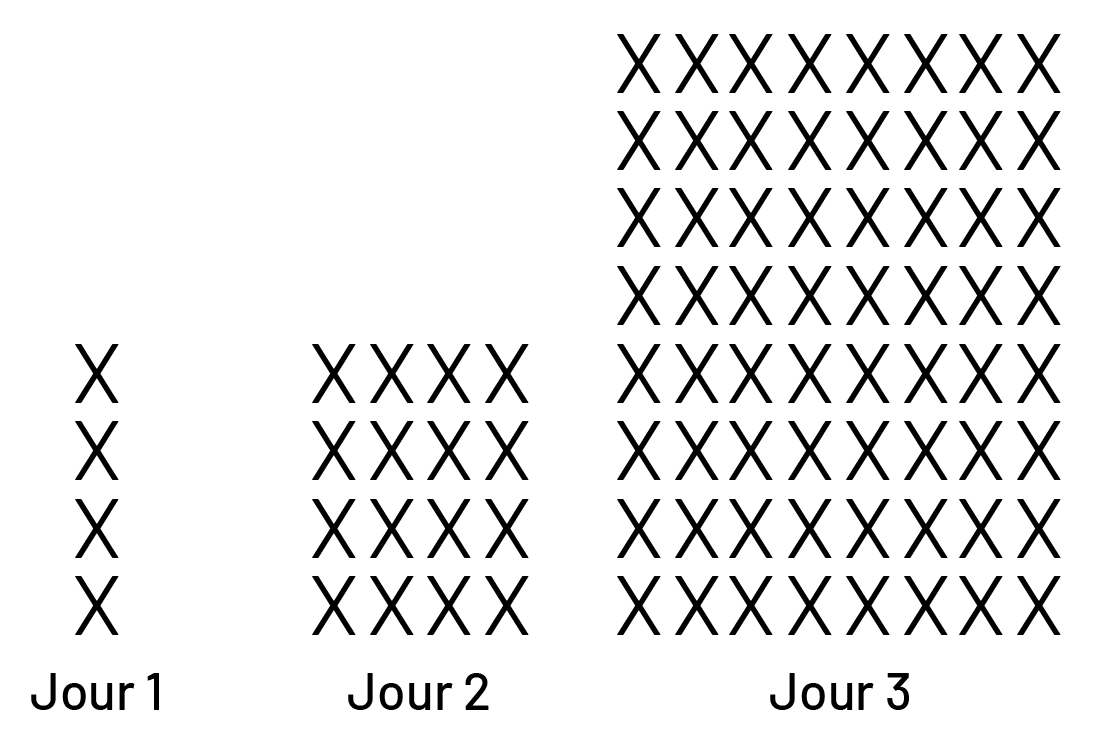
Source : inspiré de En avant, les maths!, 5e année, ML, Algèbre, p. 20.
Activité 2 : est-il plus long de sortir d’une pièce que d’y entrer?
Cette activité intègre des concepts des domaines Algèbre et Données. Elle donne l’occasion aux élèves de voir deux représentations différentes (table de valeurs et représentation graphique) de situations semblables.
Présenter la situation suivante :
Le personnel enseignant distribue une copie de l’annexe Entrée et sortie aux élèves et leur demande de compléter les deux représentations en respectant les régularités de chacune. Ensuite, il les invite à examiner chacune des représentations et à formuler certaines observations.
Voici quelques observations possibles :
- Les deux types de représentations diffèrent, la première est une table de valeurs, l’autre, une représentation graphique.
- À l’entrée, le nombre d’élèves dans le gymnase croît, tandis qu’à la sortie, il décroît.
- Vingt-cinq élèves à la minute entrent dans le gymnase.
- Le nombre d’élèves dans le gymnase avant le début de la sortie est 300.
- Trente élèves à la minute sortent du gymnase.
- Le temps requis pour faire sortir l’ensemble des élèves du gymnase est plus court que pour les y faire entrer.
Le personnel enseignant demande ensuite aux élèves de représenter l’entrée des élèves à l’aide d’une représentation graphique, et la sortie, à l’aide d’une table de valeurs.
Note : En explorant les deux représentations d’une même situation simultanément, les élèves voient plus facilement le lien entre les données dans la table de valeurs et celles de la représentation graphique. Les représentations graphiques favorisent la visualisation d’un ensemble de données numériques; elles aident donc à voir s’il s’agit d’une situation de croissance ou de décroissance et s’il y a une régularité.
En groupe-classe, le personnel enseignant approfondit la situation en faisant ressortir certains éléments importants et certaines relations.
Voici quelques suggestions de questions pour stimuler cet échange, lesquelles varient en fonction du cheminement des élèves en algèbre :
- Laquelle des deux représentations trouvez-vous plus claire visuellement? Pourquoi? (La représentation graphique permet de voir rapidement s’il s’agit d’une situation de croissance ou de décroissance. On voit aussi qu’il y a une régularité.)
- S’il y avait davantage d’élèves, combien d’élèves seraient entrées et entrés dans le gymnase après 15 minutes? Pouvez-vous le déterminer à l’aide de la représentation graphique? (Selon l’augmentation, on voit qu’après 15 minutes, il y aurait 375 élèves dans le gymnase.)
- Peux-tu expliquer, dans tes mots, la règle qui représente la relation entre le nombre d’élèves dans le gymnase et le temps écoulé depuis le début de leur entrée dans celui-ci? (Pour déterminer le nombre d’élèves dans le gymnase à un certain moment, on doit multiplier le temps écoulé par 25.)
- Est-ce que la même règle peut être utilisée pour représenter la relation entre le nombre d’élèves dans le gymnase et le temps écoulé depuis le début de la sortie des élèves? Explique ton raisonnement. (Non, car le temps requis pour l’entrée au gymnase n’est pas le même que celui requis pour la sortie.)
- Quelle règle représente la relation entre le nombre d’élèves dans le gymnase et le temps écoulé depuis le début de la sortie? (Pour déterminer le nombre d’élèves dans le gymnase après un certain nombre de minutes du début de la sortie, on doit multiplier le temps écoulé par 30, puis soustraire ce produit du nombre d’élèves qu’il y avait dans le gymnase au départ, soit 300.)
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 107-108.
Activité 3 : vive le papier recyclé!
Le personnel enseignant anime une discussion en groupe-classe sur les enjeux écologiques relatifs à la production de papier et à une saine exploitation forestière. Cet échange sera l’occasion de discuter de la relation entre la fabrication de papier recyclé et la protection des forêts. Le personnel enseignant soumet la situation ci-dessous afin de sensibiliser les élèves aux avantages d’utiliser du papier recyclé :
On estime qu’en moyenne, la production de 10 000 feuilles de papier recyclé sauve un arbre. Pour cette raison, le personnel d’une école a choisi de se servir exclusivement de papier recyclé et a comptabilisé, de façon cumulative, le nombre de feuilles de papier utilisées à la fin de chacun des trois premiers mois.
Au terme du premier mois, 10 000 feuilles ont été utilisées. Après le deuxième mois, c’est 15 000 feuilles qui ont été utilisées, après le troisième mois, 20 000 feuilles.
En groupe-classe, le personnel enseignant pose diverses questions pour faire ressortir les différentes relations que la situation présente :
- Combien de feuilles auront été utilisées après le quatrième et le cinquième mois, si la consommation demeure constante (donc si la régularité est maintenue)?
- Si la régularité est maintenue, combien de feuilles auront été utilisées après 10 mois?
Les élèves peuvent représenter la relation entre le nombre de mois et le nombre de feuilles utilisées à l’aide d’une table de valeurs.
| Nombre de mois (n) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| Nombre total de feuilles utilisées (f) | 10 000 | 15 000 | 20 000 | 25 000 | 30 000 | 35 000 | 40 000 | 45 000 | 50 000 | 55 000 |
Poursuivre l’échange avec les questions suivantes :
- Combien d’arbres a-t-on sauvés après un mois en utilisant du papier recyclé au lieu de papier non recyclé? (Un arbre a été sauvé.)
- Combien d’arbres a-t-on sauvés au bout d’une année scolaire (10 mois) si on a utilisé du papier recyclé? (Cinq arbres et demi ont été sauvés.)
- Quelle règle pourrait décrire la relation entre le nombre d’arbres sauvés et le nombre de feuilles utilisées? (Le nombre d’arbres sauvés correspond au nombre de feuilles utilisées divisé par 10 000.) La table de valeurs ci-dessous pourrait aussi représenter cette relation.
| Nombre total de feuilles utilisées (f) | 10 000 | 15 000 | 20 000 | 25 000 | 30 000 | 35 000 | 40 000 | 45 000 | 50 000 | 55 000 |
|---|---|---|---|---|---|---|---|---|---|---|
| Nombre d’arbres sauvés (a) | 1 | 1,5 | 2 | 2,5 | 3 | 3,5 | 4 | 4,5 | 5 | 5,5 |
Note : Les élèves auront peut-être tendance à croire que le nombre d’arbres sauvés est peu élevé (en un an, cette école aurait sauvé moins de six arbres). Par contre, en plaçant le geste dans un contexte global (si chaque école utilise exclusivement du papier recyclé à 100 %), les élèves saisiront mieux l’avantage de cette pratique responsable.
Afin d’amener les élèves à saisir ce que représentent de telles quantités de feuilles, le personnel enseignant leur montre une boîte de papier et présente la relation entre le nombre de paquets dans la boîte et le nombre de feuilles qu’elle contient (10 paquets de 500 feuilles, soit 5 000 feuilles). Le personnel enseignant pose des questions afin de les inciter à créer une table de valeurs qui représente la relation entre un nombre quelconque de paquets de feuilles et le nombre total de feuilles correspondant, et une autre qui représente la relation entre un nombre quelconque de paquets de feuilles et le nombre de boîtes correspondant.
Voici quelques suggestions de questions à poser :
- Combien de paquets 2 000 feuilles de papier représenteraient-elles? 3 000 feuilles? 10 000 feuilles?
- Comment peut-on déterminer le nombre de paquets que représentent un nombre de feuilles donné?
- Combien de paquets de feuilles y aura-t-il dans deux boîtes? trois boîtes? 10 boîtes?
- Comment peut-on déterminer le nombre de paquets de feuilles dans un nombre de boîtes donné?
- Combien de boîtes de papier recyclé l’école en question a-t-elle utilisées? (L’école a utilisé 11 boîtes de papier recyclé.)
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 110-112.
Note : Animer une discussion sur l’importance de faire des choix éclairés afin de protéger et conserver l’environnement. Faire réfléchir les élèves aux moyens qui peuvent être utilisées pour réduire la consommation de papier recyclé.
