C1.3 Déterminer et utiliser des règles pour prolonger des suites, faire et justifier des prédictions, et trouver des termes manquants dans des suites à motif répété et des suites croissantes et décroissantes.
Habileté : déterminer et utiliser les règles pour prolonger des suites, faire et justifier des prédictions et trouver des termes manquants
L’étude des relations inclut la représentation de relations par des règles énoncées en langage courant.
Il est plus difficile de déterminer une règle de correspondance que de déterminer une règle de régularité. La détermination de la règle de correspondance en langage courant est une étape importante dans le développement de la pensée algébrique puisqu’il s’agit d’une généralisation de la relation. La règle de correspondance permet aux élèves d’expliquer la relation entre les deux quantités en changement et de déterminer n’importe quel terme (par exemple, le 25e terme) sans avoir à prolonger la suite jusqu’au terme recherché.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 52.
Certaines règles peuvent servir à renforcer le sens du nombre chez les élèves, tout en développant leur pensée algébrique. Il est préférable d’utiliser des situations contextuelles, car elles sont moins abstraites. Les situations peuvent présenter une variété de règles. Voici quelques exemples.
Note : Ces situations où l’on s’intéresse d’abord à l’analyse de règles peuvent être utilisées dans un contexte de résolution de problèmes ou comme prolongement de l’apprentissage. Il est important de choisir des situations d’apprentissage qui ne sont pas nécessairement orientées vers la recherche d’une règle puisque, dans plusieurs cas, cette règle n’est pas à la portée des élèves.
Exemple 1
Dominique fait des économies pour acheter un jeu vidéo dont le prix est de 74,25 $ (taxes incluses). Or, dans son portefeuille, il n’a que 35 $. Chaque semaine, ses parents lui donnent 5 $ qu’il conserve précieusement dans son portefeuille. On peut représenter la relation entre le nombre de semaines qui passent et le nombre de dollars dans le portefeuille de Dominique par une table de valeurs.
| Nombre de semaines | 1 | 2 | 3 | |||
|---|---|---|---|---|---|---|
| Nombre de dollars dans le portefeuille | 40 | 45 | 50 |
Combien d’argent Dominique aura-t-il dans son portefeuille après 5 semaines s’il ne dépense aucun dollar ?
Règle de régularité (addition)
On peut représenter la relation entre le nombre de dollars dans le portefeuille de Dominique d’une semaine à l’autre par une table de valeurs. Chaque terme augmente d’une valeur de 5.
La règle de régularité est de +5.
J’ai prolongé la table de valeurs et j’ai déterminé qu’il aura 60 $ au bout de 5 semaines.
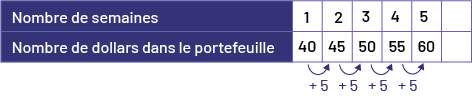image Table de
valeurs qui représente le nombre de semaines et le nombre de dollars dans le portefeuille.Semaine un : 40
dollars.Semaine 2 : 45 dollars.Semaine 3 : 50 dollars.Semaine 4 : 55 dollars.Semaine 5 : 60 dollars.Des flèches
représentent les bonds de plus 5 pour les dollars.
Règle de correspondance
On peut représenter la relation entre le nombre de semaines qui passent et le nombre de dollars dans le portefeuille à l’aide de mots.
La 1ère semaine, Dominique a 35 $ et 1 billet de 5 $ dans son portefeuille, ce qui lui donne 40 $.
La 2e semaine, Dominique a 35 $ et 2 billets de 5 $ dans son portefeuille, ce qui lui donne 45 $.
La 3e semaine, Dominique a 35 $ et 3 billets de 5 $ dans son portefeuille, ce qui lui donne 50 $.
La 4e semaine, Dominique a 35 $ et 4 billets de 5 $ dans son portefeuille, ce qui lui donne 55 $.
La 5e semaine, Dominique a 35 $ et 5 billets de 5 $ dans son portefeuille, ce qui lui donne 60 $.
Exemple 2
Un camelot doit livrer 45 journaux dans son quartier. La table de valeurs suivante représente la relation entre le nombre de minutes écoulées depuis le début de la livraison et le nombre de journaux qu’il lui reste à livrer.
| Nombre de minutes écoulées | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| Nombre de journaux à livrer | 45 | 42 | 39 | 36 | 33 |
Combien lui reste-t-il de journaux à livrer après 7 minutes ? Explique ta réponse.
Règle de régularité (soustraction)
J’ai constaté qu’il lui reste 3 journaux de moins à livrer chaque minute. Ça veut dire que le camelot livre 3 journaux chaque minute. J’ai prolongé la table de valeurs en maintenant cette règle de régularité, ce qui m’a permis de conclure qu’après 7 minutes, il lui reste 24 journaux à livrer.
image Table de valeurs qui représente le nombre de minutes écoulées et le nombre de journaux à livrer.Semaine zéro : 45 journaux.Semaine un : 42 journaux.Semaine 2 : 39 journaux.Semaine 3 : 36 journaux.Semaine 4 : 33 journaux.Semaine 5 : 30 journaux.Semaine 6 : 27 journaux.Semaine 7 : 24 journaux.Des flèches représentent les bonds de moins 3 pour les journaux.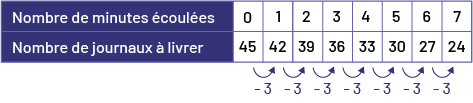
Exemple 3
Émilie garde régulièrement des enfants. Un couple lui demande de garder leur enfant 6 heures par jour pendant 10 jours et lui offre de la payer selon la table de valeurs suivante.
| Rang (jour) | 1 | 2 | 3 | 4 | … |
|---|---|---|---|---|---|
| Salaire pour la journée ($) | 1 | 2 | 4 | 8 | … |
Si elle accepte l’offre, combien d’argent Émilie gagnera-t-elle en tout ?
Règle de régularité (multiplication)
J’ai remarqué que le salaire double chaque jour. J’ai prolongé la table de valeurs jusqu’à 10 jours. J’ai ensuite additionné les salaires et j’ai trouvé qu’Émilie gagnerait au total 1 023 $ pour 10 jours de gardiennage.
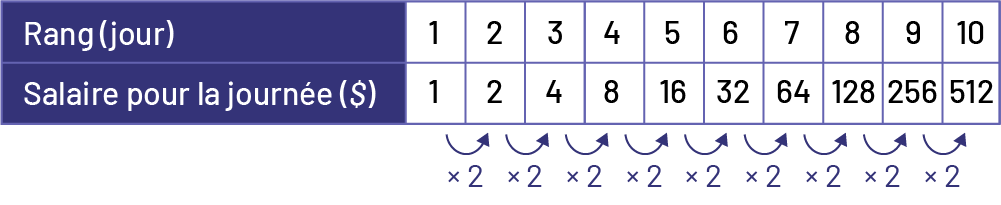image Table de
valeurs représentant le rang en jour et le salaire pour la journée en dollars.Rang un : un dollar.Rang 2 :2
dollars.Rang 3 : 4 dollars.Rang 4 : 8 dollars.Rang 5 : 16 dollars.Rang 6 : 32 dollars.Rang 7 : 64 dollars.Rang 8 : 128
dollars.Rang 9 : 256 dollars.Rang dix : 512 dollars.Des flèches représentent les bonds de fois 2 des dollars.
Exemple 4
Dans le cadre d’un tournoi de soccer, 64 équipes sont présentes. Le premier jour, toutes les équipes jouent un match et les équipes perdantes sont éliminées. Le deuxième jour, les 32 équipes qui restent jouent un match et les équipes perdantes sont éliminées. Il en est de même chaque jour qui suit.
Construis une table de valeurs qui représente la relation entre le rang (jour) et le nombre d’équipes qui jouent un match ce jour-là.
Règle de régularité (division)
J’ai remarqué que le nombre d’équipes qui jouent un match diminue de la moitié à chaque jour. La règle de régularité est donc ÷ 2.
image Table de valeurs qui représente le rang en jour et le nombre d’équipes qui jouent un match. Rang un : 64 équipes. Rang 2 : 32 équipes.Rang 3 : 16 équipes. Rang 4 : 8 équipes. Rang 5 : 4 équipes. Rang 6 : 2 équipes. Des flèches représentent les bonds de diviser par 2.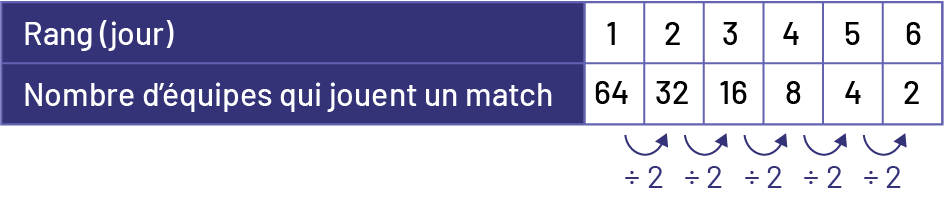
Quel jour aura lieu le dernier match ?
Le dernier match aura lieu au cours de la 6e journée.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 35-37.
Il est important de reconnaître que le cheminement vers l’expression d’une règle peut différer d’une ou d’un élève à l’autre, puisque le raisonnement se développe à partir de perceptions individuelles. L’exemple suivant, inspiré d’une recherche de Radford (2006, p. 2-21), illustre comment des élèves peuvent percevoir différemment la relation entre le rang de la figure dans une suite non numérique à motif croissant et le nombre de cercles qui le composent.
Exemple
image Dans un encadré on peut lire : « Je vois 2 rangées de cercles. Dans la
rangée supérieure, il y a toujours un cercle de plus, en bleu, que le rang de la figure et dans la rangée du bas, il y
a toujours 2 cercles de plus, en gris, que le rang de la figure. »Suite, non numérique à motifs croissants.Rang un, 5
cercles, 2 jaunes, un bleu 2 gris.Rang 2, 7 cercles, 4 jaunes, un bleu 2 gris.Rang 3, 9 cercles, 6 jaunes, un bleu 2
gris.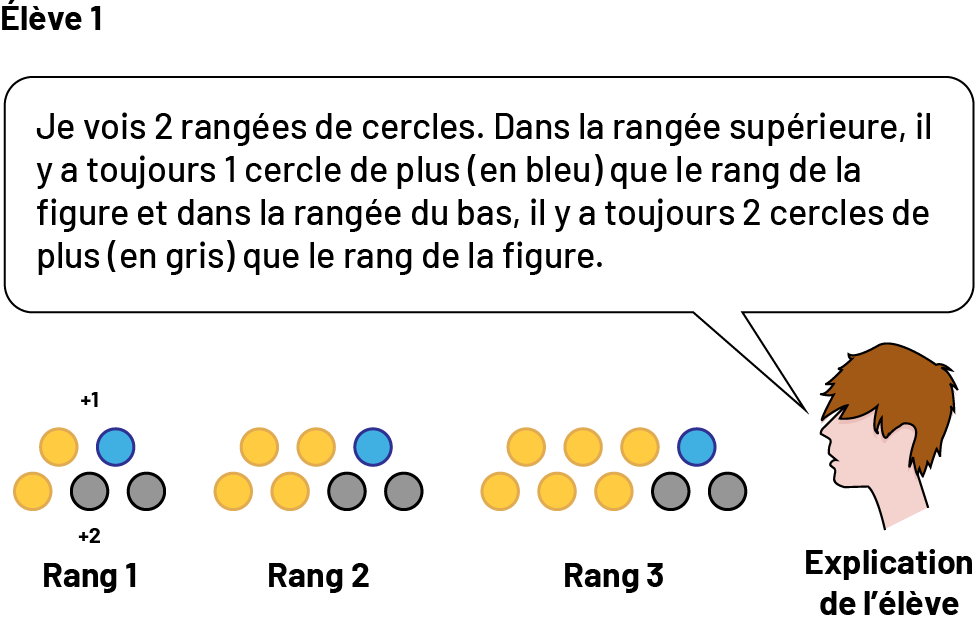
En poursuivant son analyse, l’élève détermine que la figure au 10e rang contiendra (10 + 1) + (10 + 2) cercles, soit 23 cercles.
image Dans un encadré on peut lire : « Pour trouver le nombre total de cercles, tu additionnes deux fois le rang de la figure et tu ajoutes 3. Donc, pour le rang un, la phrase mathématique est : un plus un, plus 3 égal, 5 ; pour le rang 2 : 2 plus 2, plus 3 égal 7 et pour le rang 3 : 3 plus 3, plus 3 égal 9.»Suite, non numérique à motifs croissants.Rang un, 5 cercles, 2 jaunes, 3 bleus.Rang 2, 7 cercles, 4 jaunes, 3 bleus.Rang 3, 9 cercles, 6 jaunes, 3 bleus.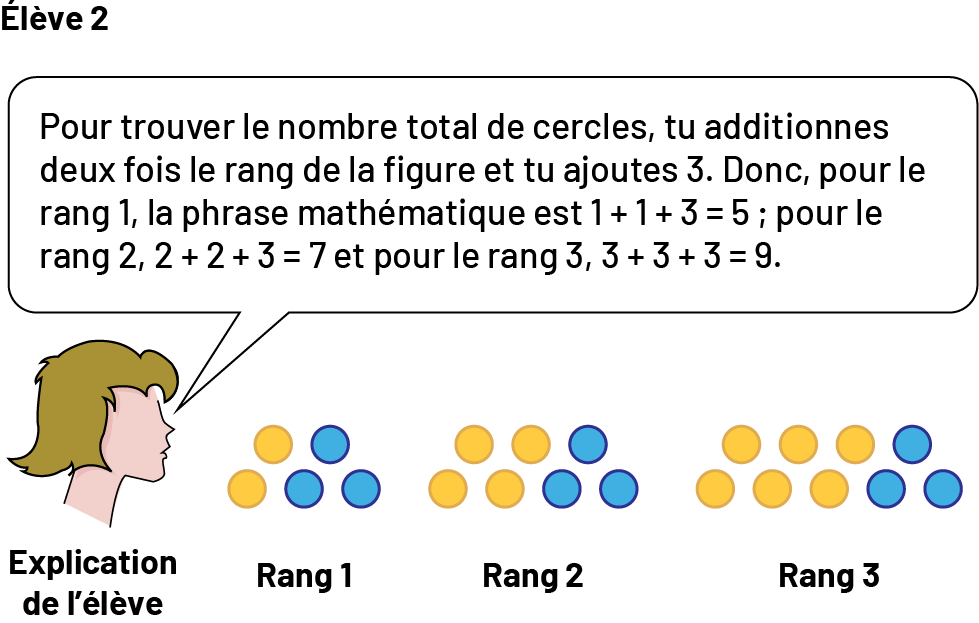
image Dans un encadré on peut lire : « Dans le rang un, je vois 5 cercles. Dans le rang 2, je vois les
5 cercles initiaux, auxquels on a ajouté un groupe de 2 cercles. Dans le rang 3, je vois les 5 cercles initiaux,
auxquels on a ajouté 2 groupes de 2 cercles. »Suite, non numérique à motifs croissants.Rang un, 5 cercles.Rang 2, 7
cercles, 5 jaunes, 2 bleus.Rang 3, 9 cercles, 5 jaunes, 4 bleus.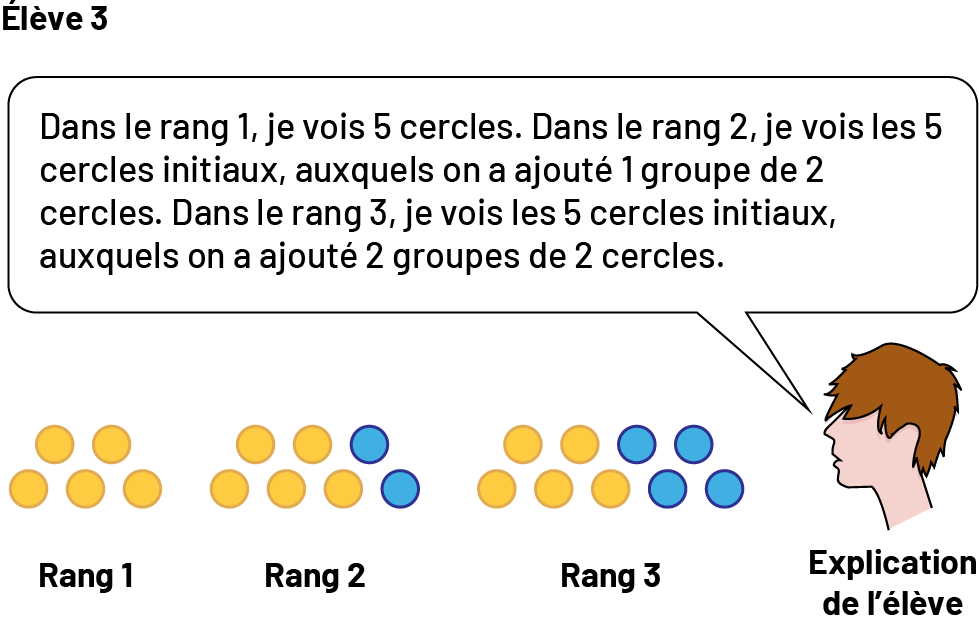
Note : L’élève peut présenter son interprétation à l’aide d’un tableau.
| Rang de la figure | Nombre de cercles | Explication à l'aide de la régularité | Relation entre le rang de la figure et le nombre de cercles qui la composent |
|---|---|---|---|
| 1 | 5 | 5 | 5 + 0 x 2 |
| 2 | 7 | 5 + 2 | 5 + 1 x 2 |
| 3 | 9 | 5 + 2 + 2 | 5 + 2 x 2 |
| 4 | 11 | 5 + 2 + 2 + 2 | 5 + 3 x 2 |
| 25 | ? | 5 + 2 + 2 + 2 + ... | 5 + 24 x 2 |
Les règles formulées par les trois élèves proviennent de leur compréhension de cette relation. Chaque élève a perçu et généralisé la situation à sa façon, ce qui a engendré trois règles exprimées en mots différents, mais équivalents. Aucune n’est meilleure qu’une autre. Elles démontrent toutefois que l’interprétation que les élèves se font d’une relation a un effet sur la règle qu’elles et ils formulent. Il est important que le personnel enseignant encourage ces différentes formulations d’une règle.
Un certain nombre d’élèves passent trop rapidement de la suite non numérique à la table de valeurs correspondante. Par exemple, à partir de la suite non numérique précédente, des élèves établissent immédiatement la table suivante.
| Rang de la figure | 1 | 2 | 3 |
|---|---|---|---|
| Nombre de cercles | 5 | 7 | 9 |
Les élèves procèdent ensuite par tâtonnements pour déterminer la règle qui définit la relation, comme en font foi les explications de l’élève ci-dessous. Dans chaque cas, il y a lieu de remettre en question la profondeur de la compréhension qu’ont ces élèves de la relation qu’elle représente.
image Dans un
encadré on peut lire : « Pour trouver le nombre total de cercles, tu additionnes deux fois le rang de la figure et tu
ajoutes 3. Donc, pour le rang un, la phrase mathématique est : un plus un, plus 3 égal, 5 ; pour le rang 2 : 2 plus 2,
plus 3 égal 7 et pour le rang 3 : 3 plus 3, plus 3 égal 9.»Suite, non numérique à motifs croissants.Rang un, 5
cercles, 2 jaunes, 3 bleus.Rang 2, 7 cercles, 4 jaunes, 3 bleus.Rang 3, 9 cercles, 6 jaunes, 3 bleus.
Le personnel enseignant doit tenir compte des différentes façons qu’ont les élèves de percevoir les relations entre les termes d’une suite et adapter son questionnement en conséquence afin d’aider chaque élève à exprimer la règle en mots avec précision. La situation qui suit met en évidence des exemples de questionnement adapté.
Exemple
Le personnel enseignant présente la suite de figures suivante.
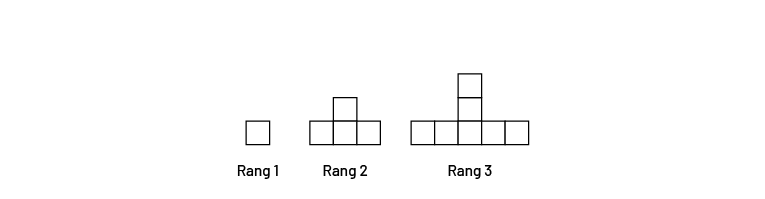
À l’aide des questions suivantes, il incite les élèves à analyser la suite et à établir une relation entre le rang de la figure et le nombre de carrés qui le composent :
- Combien de carrés composent les figures aux rangs 1, 2 et 3?
- Combien de carrés faut-il pour créer la figure au rang 4? Créez cette figure.
- Combien de carrés faut-il pour créer la figure au rang 5? Créez cette figure.
- Quelle règle voyez-vous dans le nombre de carrés?
- Créez une table de valeurs qui représente la relation entre le rang de la figure et le nombre de carrés qui le composent. Quelle règle voyez-vous dans la table?
- Combien y aura-t-il de carrés dans la figure au 6e rang? Au 10e rang? Comment le savez-vous?
- Y a-t-il d’autres façons de le déterminer?
Le personnel enseignant anime ensuite un échange mathématique qui met l’accent sur les différentes perceptions qu’ont les élèves de la relation, afin d’amener les élèves à expliquer et à verbaliser leur stratégie et leur règle, il pose des questions telles que :
- Avez-vous trouvé une méthode rapide pour compter le nombre de carrés de la figure au rang 4? Pouvez-vous nous l’expliquer?
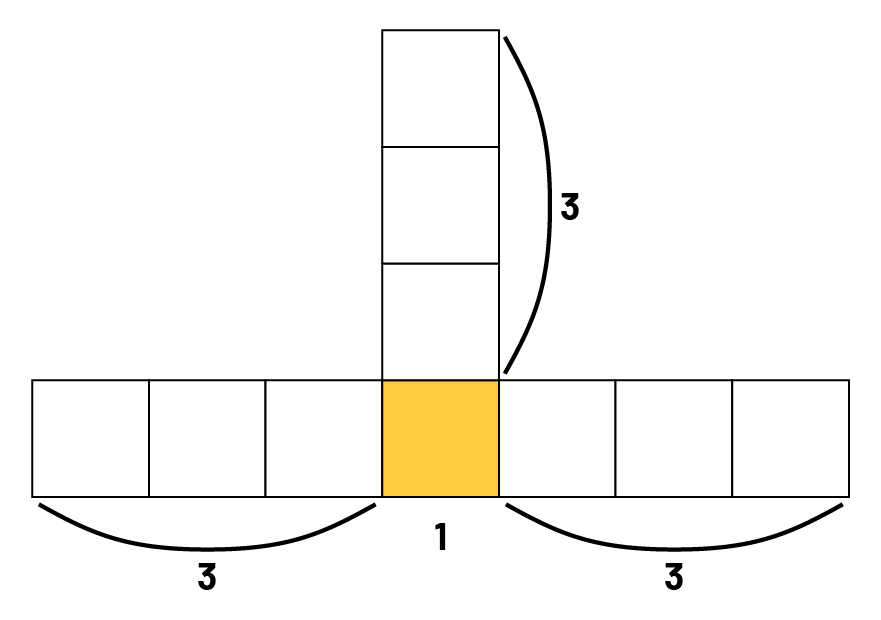
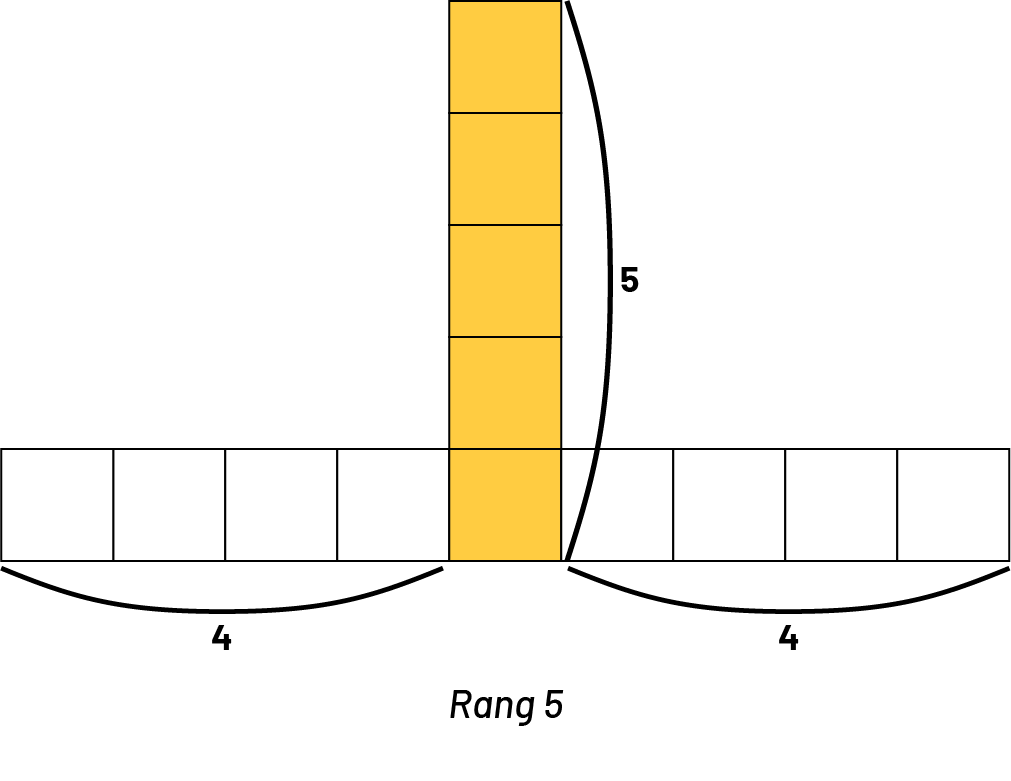
Élève 1 : Dans la figure au rang 4, je vois qu’il y a 3 carrés à gauche, 3 carrés à droite, 3 carrés au-dessus du centre et 1 au centre. En tout, ça fait 3 + 3 + 3 + 1, soit 10 carrés.
- Qui a utilisé la même méthode? Y a-t-il quelqu’un qui a utilisé une autre méthode?
Élève 2 : J’ai utilisé une méthode semblable. Je vois 1 carré au centre, et 3 branches de 3 carrés. En tout, ça fait 10 carrés.
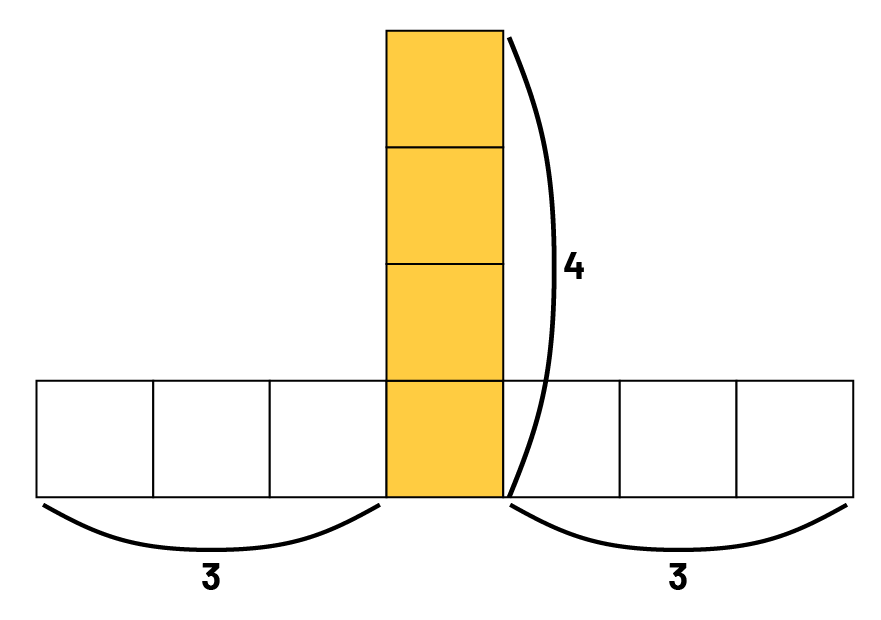
Élève 3 : Ma méthode est différente, mais j’ai obtenu la même réponse. Je vois une colonne de 4 carrés, puis 3 carrés à gauche et 3 carrés à droite. En tout, je compte 4 + 3 + 3, soit 10 carrés.
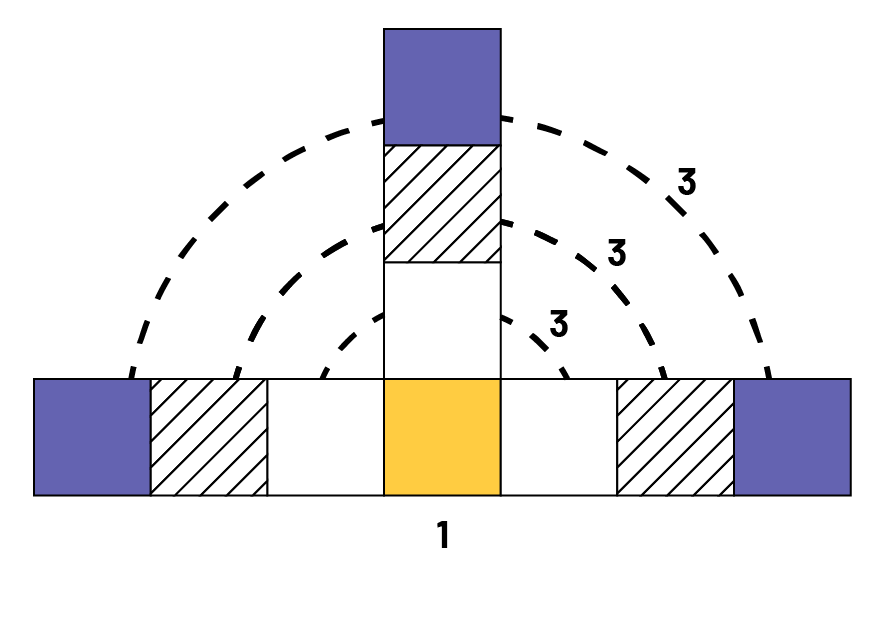
Élève 4 :Je vois les figures d’une autre façon. Si je regarde la suite, elle commence par un carré et, à chaque rang suivant, on ajoute un carré à 3 endroits. Dans la figure 4, on a ajouté les 3 carrés 3 fois. En tout, on a 10 carrés.
- Votre méthode fonctionne-t-elle pour compter le nombre de carrés de la figure au rang 5?
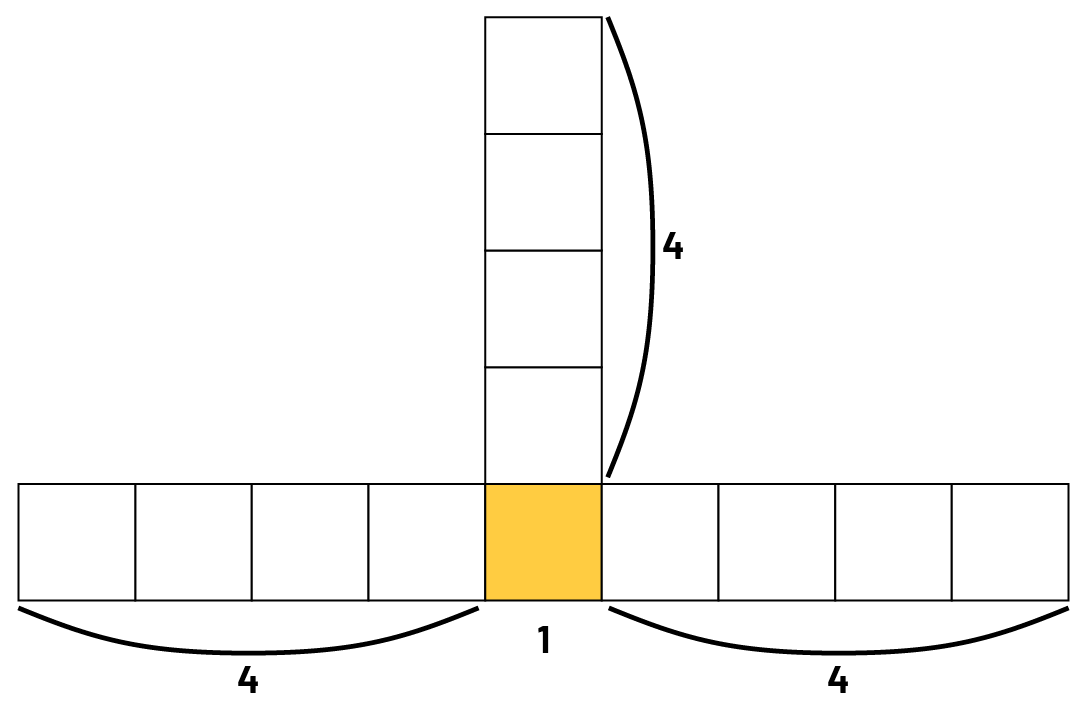
Élève 1 : Oui. Je vois qu’il y a 4 carrés à gauche, 4 carrés à droite, 4 carrés vers le haut et un carré au centre. En tout, ça fait 4 + 4 + 4 + 1, soit 13 carrés.
Élève 2 : Oui. Je vois 1 carré au centre, et 3 branches de 4 carrés. En tout, ça fait 13 carrés.
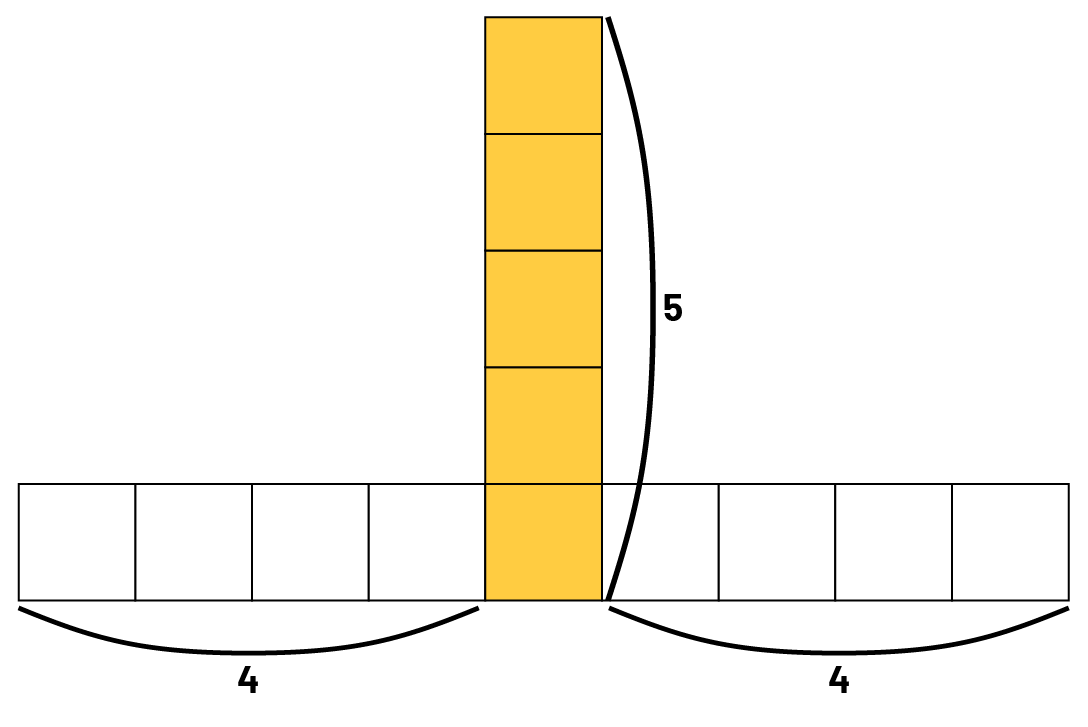
Élève 3 : Oui. Je vois une colonne de 5 carrés, puis 4 carrés à gauche et 4 carrés à droite. En tout, je compte 5 + 4 + 4, soit 13 carrés.
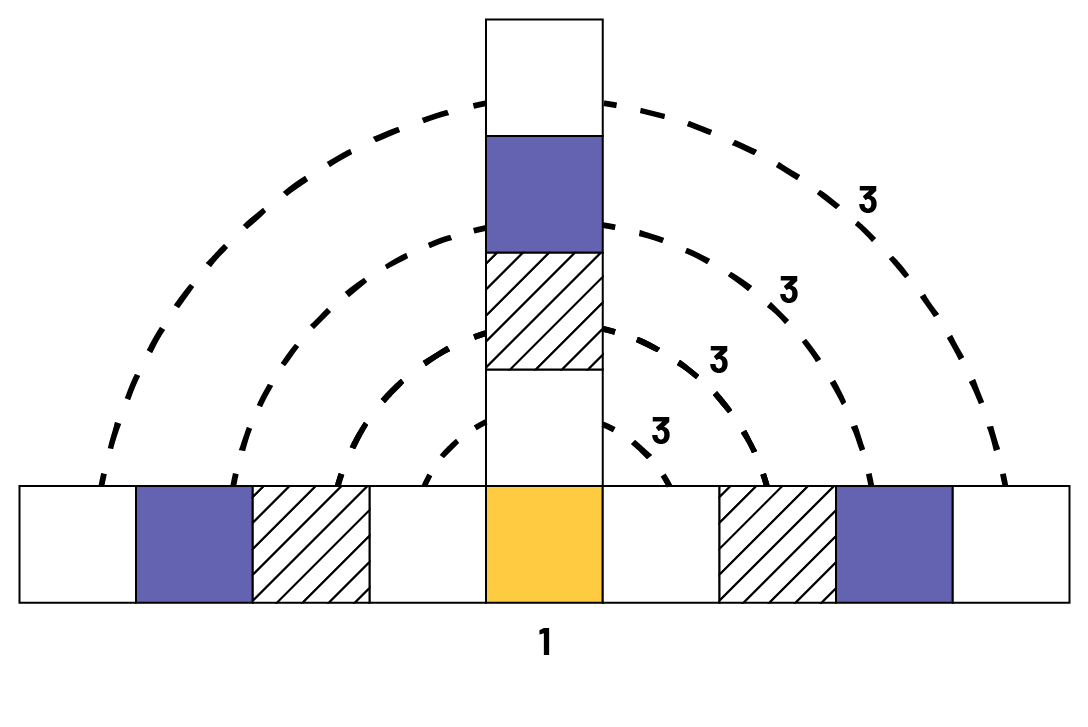
Élève 4 : Oui. Si je regarde la suite, elle commence par un carré et, à chaque figure suivante, on ajoute un carré à 3 endroits. Dans la figure au rang 5, on a ajouté les 3 carrés 4 fois. En tout, on a 13 carrés.
- Selon votre méthode, combien de carrés y aura-t-il dans la figure au rang 10?
Élève 1 : Il y aura 28 carrés. Il y aura 1 carré au centre, puis 9 carrés à gauche, 9 carrés à droite et 9 carrés au-dessus du centre. En tout, il y aura 9 + 9 + 9 + 1, soit 28 carrés.
- Comment sais-tu combien il y en aura à gauche, à droite et vers le haut?
Élève 1 : D’après les premières figures de la suite, il y a toujours 1 carré de moins que le rang de la figure à chacun de ces trois endroits.
Élève 2 : C’est presque la même chose.
- Pourquoi dis-tu que c’est la même chose que l’autre stratégie (élève 1)?
Élève 2 : Lui (élève 1), il mentionne qu’il additionne 9 + 9 + 9. Moi, je dis que je multiplie, c’est-à-dire que je fais 3 × 9, car multiplier, c’est comme additionner plusieurs fois une même quantité.
Élève 3 : J’ai aussi obtenu 28, puisqu’il y aura une colonne de 10 carrés, puis 9 carrés à gauche et 9 carrés à droite, donc 10 + 9 + 9 = 28 carrés.
- Comment sais-tu que c’est bien 10 carrés, puis 9 carrés deux fois?
Élève 3 : D’après les premières figures de la suite, le nombre de carrés dans la colonne est égal au rang de la figure, et le nombre de carrés à gauche et à droite est toujours 1 de moins que le rang.
Élève 4 : D’après ma façon de voir les figures, il y aura 1 carré au centre. Ensuite, on ajoute chaque fois 3 carrés pour passer au rang suivant. On doit le faire pour les rangs 2 à 10, soit 9 fois. En tout, on aura alors 1 + (9 × 3), ou 28 carrés.
Note : On remarque que les calculs effectués sont similaires. Cependant, les différentes façons de voir l’organisation des carrés dans la figure et l’expression de cette organisation ont généré des règles différentes, mais équivalentes.
- Votre méthode rapide de compter (votre règle) peut-elle être utilisée pour déterminer le nombre de carrés qu’il y aura dans la figure au rang 25?
En expliquant au moyen de mots la façon de déterminer la valeur d’un terme éloigné (par exemple, la figure au rang 10 ou 25) en relation avec le rang d’une figure, les élèves utilisent leur règle pour interpréter la relation.
Comme les élèves ont souvent de la difficulté à déterminer les quantités en jeu, le personnel enseignant pose ensuite des questions telles que celles ci-dessous afin de les amener à communiquer leur règle plus clairement et à exprimer la relation à l’aide de mots.
- Comment pouvez-vous déterminer le nombre de carrés qui composent une figure à n’importe quel rang?
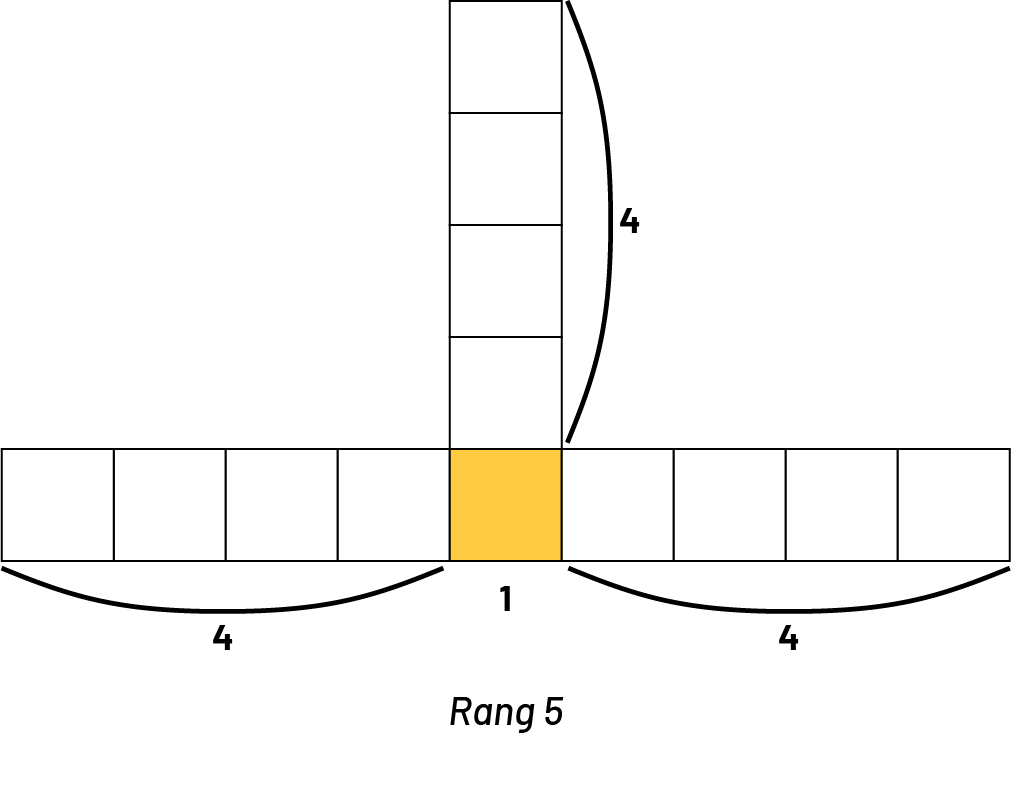
Élève 1 : Pour déterminer le nombre de carrés qui composent une figure à n’importe quel rang, j’additionne un nombre 3 fois, puis 1.
- Quel est ce nombre? Comment peux-tu l’identifier ou le nommer?
Élève 1 : C’est toujours le numéro du rang précédent.
- Peux-tu alors exprimer ta règle pour déterminer le nombre de carrés qui composent une figure à n’importe quel rang avec plus de précision?
Élève 1 : Pour déterminer le nombre de carrés qui composent une figure à n’importe quel rang, j’additionne le numéro du rang précédent 3 fois, puis 1.
Élève 2 : Pour déterminer la valeur de n’importe quel terme, je multiplie par 3 et j’ajoute 1.
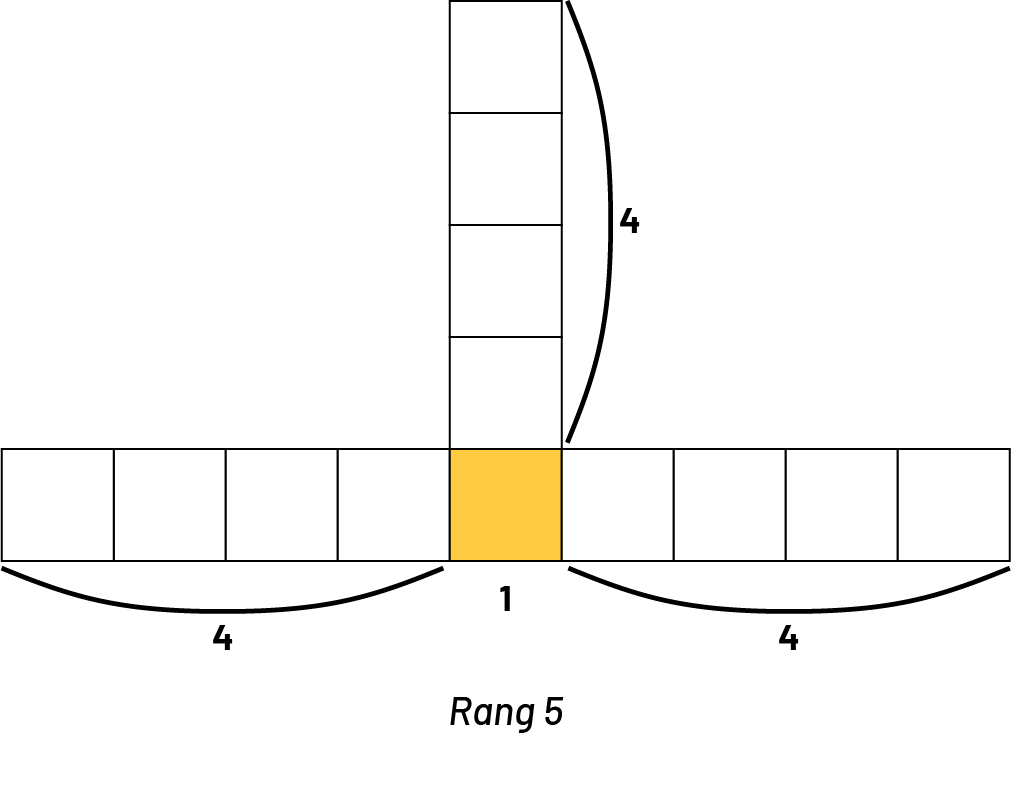
- Qu’est-ce que tu multiplies par 3? Qu’est-ce que tu détermines?
Élève 2 : Je multiplie le rang de la figure précédente par 3 et j’ajoute 1. Cela me donne le nombre de carrés qui composent la figure en question.
Élève 3 : Dans chaque figure, il y a toujours 3 branches. Une branche qui a le même nombre de carrés que le rang de la figure et deux autres qui ont 1 carré de moins que le rang de la figure. Pour déterminer le nombre de carrés, j’additionne ces 3 nombres.
- Peux-tu m’expliquer cette règle de façon plus concise?
Élève 3 : Pour déterminer le nombre de carrés qui composent une figure à un rang quelconque, j’additionne 3 valeurs, soit le rang de la figure et deux fois le rang de la figure précédente.
Élève 4 : Je fais 3 fois un nombre pour déterminer le nombre de carrés sur les 3 branches et j’ajoute 1 pour celui qui est au centre. En fait, je multiplie le rang de la figure précédente par 3 et j’ajoute 1.
Le personnel enseignant invite ensuite les élèves à vérifier la validité de leur règle. Pour valider les règles, on utilise la table de valeurs.
L’exemple précédent suit une certaine démarche qui peut être résumée comme suit : demander aux élèves de prolonger la suite de figures, d’analyser la régularité et de la décrire, de créer une table de valeurs, puis de formuler une règle en mots. Cette démarche permet d’explorer toutes sortes de relations, même certaines qui peuvent, au premier abord, sembler être hors de la portée des élèves.
Exemple
Voici une suite décroissante de figures. On étudie la relation entre le nombre de carrés qui composent chaque figure à chaque rang.
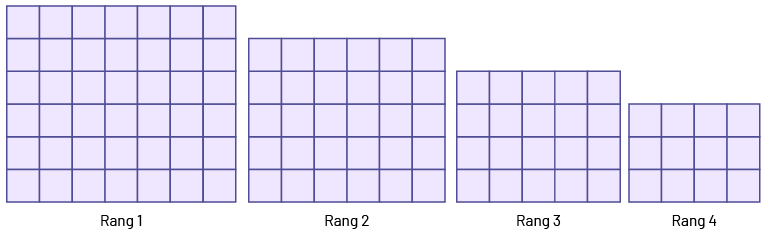
À première vue, cette situation peut sembler très complexe, puisque la suite correspondant au nombre de carrés qui composent chaque figure (42, 30, 20, 12…) ne présente pas une simple régularité de soustraction. Avant de mettre une telle situation de côté, il faut l’examiner de plus près. Ainsi, on peut d’abord prolonger la suite de figures, puis analyser la régularité et créer une table de valeurs comme suit.
Prolongement de la suite de figures
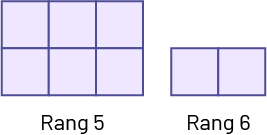
Analyse de la régularité
Si on examine les figures, on constate qu’il y a une régularité, puisqu’on enlève toujours une colonne et une rangée.
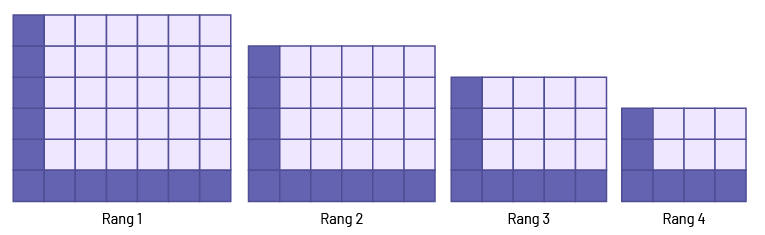
Le nombre de carrés diminue de 12, puis de 10, de 8, et ainsi de suite. On peut voir ces quantités dans la suite non numérique. Pour passer de la figure au rang 1 à la figure au rang 2, on enlève 12 carrés, soit 1 rangée de 6 carrés et 1 colonne de 6 carrés. Pour passer de la figure au rang 2 à la figure au rang 3, on enlève 10 carrés, soit 1 rangée de 5 carrés et 1 colonne de 5 carrés. Pour passer de la figure au rang 3 à la figure au rang 4, on enlève 8 carrés, soit 1 rangée de 4 carrés et 1 colonne de 4 carrés.
Création d’une table de valeurs
La table de valeurs permet de représenter cette régularité.
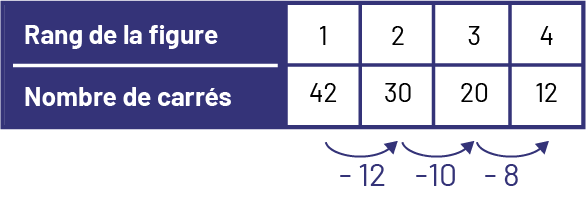
Prolonger une suite décroissante
Les élèves peuvent expliquer leurs observations comme suit :
- La figure au rang 1 est composée de 7 colonnes de 6 carrés.
- La figure au rang 2 est composée de 6 colonnes de 5 carrés.
- La figure au rang 3 est composée de 5 colonnes de 4 carrés.
Pour prolonger la suite, l’élève se rend compte que la figure au rang 5 sera composée de 3 colonnes de 2 carrés.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 54-65.
Connaissance : règles
Règle de régularité : règle qui permet de prolonger une suite en respectant la différence entre les termes (aussi appelée bond constant).
Règle de correspondance : règle qui permet de prolonger une suite en établissant la relation entre le rang et son terme.
Source : Curriculum de l’Ontario. Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l’Éducation de l’Ontario.
Suite non numérique à motif répété
Exemple de règle de correspondance en mots :
- Si le rang est un multiple de 3, le terme est un triangle.
- Si le rang donne un reste de 1 lorsqu’on le divise par 3, le terme est un rectangle.
- Si le rang donne un reste de 2 lorsqu’on le divise par 3, le terme est un trapèze.
Suite non numérique à motif croissant
Suite C
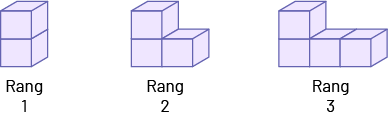
Exemple d’une règle de correspondance en mots :
- Chaque terme est composé d’une colonne de 2 cubes, à laquelle on ajoute 1 cube de moins que le rang de la figure.
Suite non numérique à motif décroissant
Suite D
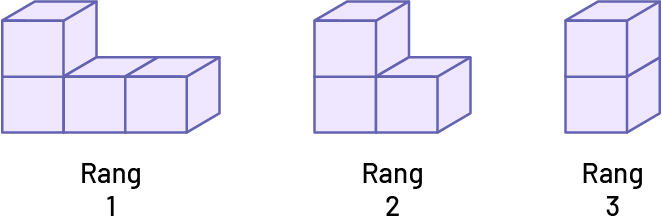
Exemple d’une règle de régularité en mots :
- Chaque terme est composé d’une colonne de 2 cubes. On enlève 1 cube à chaque rang.
Suite numérique croissante
4, 8, 16, 32, 64
Exemple d’une règle de régularité en mots et en symboles :
- On double la valeur du terme pour obtenir le terme suivant. La règle est donc : × 2.