C1.3 Déterminer et utiliser les règles pour prolonger des suites, faire et justifier des prédictions, et trouver les termes manquants dans des suites à motif répété, des suites croissantes et des suites décroissantes, et utiliser les représentations symboliques des règles pour trouver des valeurs inconnues dans des suites croissantes linéaires.
Habileté : déterminer et utiliser les règles pour prolonger des suites, faire et justifier des prédictions, et trouver les termes manquants
L’étude des relations comprend la représentation de relations au moyen des règles énoncées en langage courant.
Il est plus difficile de déterminer une règle de correspondance que de déterminer une règle de régularité. La détermination de la règle de correspondance en langage courant est une étape importante dans le développement de la pensée algébrique, puisqu’il s’agit d’une généralisation de la relation. La règle de correspondance aide les élèves à expliquer la relation entre les deux quantités en changement et à déterminer n’importe quel terme, comme le 25e, sans devoir prolonger la suite jusqu’au terme recherché.
Les élèves apprennent à représenter une règle de correspondance exprimée en mots à l’aide d’une équation. Elles et ils doivent choisir les variables et formuler une équation qui représente la règle, ce qui contribue au développement du sens du symbole. C’est dans un tel contexte que les équations obtenues et les relations qu’elles représentent prennent tout leur sens.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 52.
Certaines règles peuvent servir à renforcer le sens du nombre chez les élèves, tout en développant leur pensée algébrique. Il est préférable d’utiliser des situations contextuelles, car elles sont moins abstraites. Les situations peuvent présenter une variété de règles.
Voici quelques exemples :
Exemple 1
Dominique fait des économies pour acheter un jeu vidéo dont le prix est de 74,25 $ (taxes comprises). Or, dans son portefeuille, il n’a que 35 $. Chaque semaine, ses parents lui donnent 5 $ qu’il conserve précieusement dans son portefeuille. On peut représenter la relation entre le nombre de semaines qui passent et le nombre de dollars dans le portefeuille de Dominique au moyen d’une table de valeurs.
| Nombre de semaines | 1 | 2 | 3 | |||
|---|---|---|---|---|---|---|
| Nombre de dollars dans le portefeuille | 40 | 45 | 50 |
a) Combien d’argent Dominique aura-t-il dans son portefeuille après 5 semaines s’il ne dépense aucun dollar?
Règle de régularité (addition)
On peut représenter la relation entre le nombre de dollars dans le portefeuille de Dominique d’une semaine à l’autre au moyen d’une table de valeurs.
J’ai prolongé la table de valeurs et j’ai déterminé qu’il aura 60 $.
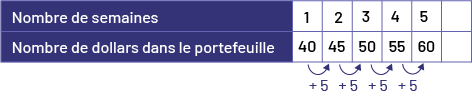 Image Table de valeurs qui représente le nombre de semaines et le nombre de dollars dans le portefeuille. Semaine un : 40 dollars. Semaine 2 : 45 dollars. Semaine 3 : 50 dollars. Semaine 4 : 55 dollars. Semaine 5 : 60 dollars. Des flèches représentent les bonds de plus 5 pour les dollars.
Image Table de valeurs qui représente le nombre de semaines et le nombre de dollars dans le portefeuille. Semaine un : 40 dollars. Semaine 2 : 45 dollars. Semaine 3 : 50 dollars. Semaine 4 : 55 dollars. Semaine 5 : 60 dollars. Des flèches représentent les bonds de plus 5 pour les dollars.
Règle de correspondance
On peut représenter la relation entre le nombre de semaines qui passent et le nombre de dollars dans le portefeuille à l’aide de mots.
- La 1re semaine, Dominique a 35 $ et 1 billet de 5 $ dans son portefeuille, ce qui lui donne 40 $.
- La 2e semaine, Dominique a 35 $ et 2 billets de 5 $ dans son portefeuille, ce qui lui donne 45 $.
- La 3e semaine, Dominique a 35 $ et 3 billets de 5 $ dans son portefeuille, ce qui lui donne 50 $.
- La 4e semaine, Dominique a 35 $ et 4 billets de 5 $ dans son portefeuille, ce qui lui donne 55 $.
- La 5e semaine, Dominique a 35 $ et 5 billets de 5 $ dans son portefeuille, ce qui lui donne 60 $.
b) Après combien de semaines Dominique aura-t-il assez d’argent pour acheter le jeu vidéo?
Règle de régularité (addition)
J’ai prolongé la table de valeurs jusqu’à ce qu’il y ait 75 $ dans le portefeuille et j’ai déterminé que ce sera après 8 semaines.
 Image Table de valeurs qui représente le nombre de semaines et le nombre de dollars dans le portefeuille. Semaine un : 40 dollars. Semaine 2 : 45 dollars. Semaine 3 : 50 dollars. Semaine 4 : 55 dollars. Semaine 5 : 60 dollars. Semaine 6 : 65 dollars. Semaine 7 : 70 dollars. Semaine 8 : 75 dollars Des flèches représentent les bonds de plus 5 pour les dollars.
Image Table de valeurs qui représente le nombre de semaines et le nombre de dollars dans le portefeuille. Semaine un : 40 dollars. Semaine 2 : 45 dollars. Semaine 3 : 50 dollars. Semaine 4 : 55 dollars. Semaine 5 : 60 dollars. Semaine 6 : 65 dollars. Semaine 7 : 70 dollars. Semaine 8 : 75 dollars Des flèches représentent les bonds de plus 5 pour les dollars.
Règle de correspondance
Le nombre de billets de 5 $ est toujours le même que le nombre de semaines qui passent, plus 35 $ qui était déjà dans son portefeuille (la constante).
Alors, la 8e semaine, Dominique a 35 $ et 8 billets de 5 $ dans son portefeuille, ce qui lui donne 75 $.
35 $ + (8 × 5 $) = 35 $ + 40 $ = 75 $
Note : Autrefois, une telle situation aurait été présentée dans le cadre d’activités de résolution de problèmes et seule la deuxième question aurait été posée. La résolution du problème aurait porté sur une méthode arithmétique, par exemple :
Dominique gagne 5 $ par semaine. Il lui manque 39,25 $. Puisque 39,25 ÷ 5 = 7,85, soit environ 8, ça lui prendra 8 semaines. Or, l’approche préconisée ici est plus algébrique, puisqu’elle mise sur la comparaison de deux quantités en changement.
Exemple 2
Un camelot doit livrer 45 journaux dans son quartier. La table de valeurs ci-dessous représente la relation entre le nombre de minutes écoulées depuis le début de la livraison et le nombre de journaux qu’il lui reste à livrer.
| Nombre de minutes écoulées | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| Nombre de journaux à livrer | 45 | 42 | 39 | 36 | 33 |
a) Combien lui reste-t-il de journaux à livrer après 7 minutes? Explique ta réponse.
Règle de régularité (soustraction)
J’ai constaté qu’il lui reste 3 journaux de moins à livrer chaque minute. Ça veut dire que le camelot livre 3 journaux chaque minute. J’ai prolongé la table de valeurs en maintenant cette règle de régularité, ce qui m’a permis de conclure qu’après 7 minutes il lui reste 24 journaux à livrer.
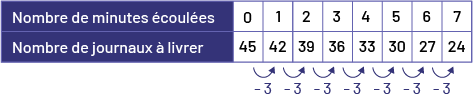 Image Table de valeurs qui représente le nombre de minutes écoulées et le nombre de journaux à livrer. Semaine zéro : 45 journaux. Semaine un : 42 journaux. Semaine 2 : 39 journaux. Semaine 3 : 36 journaux. Semaine 4 : 33 journaux. Semaine 5 : 30 journaux. Semaine 6 : 27 journaux. Semaine 7 : 24 journaux. Des flèches représentent les bonds de moins 3 pour les journaux.
Image Table de valeurs qui représente le nombre de minutes écoulées et le nombre de journaux à livrer. Semaine zéro : 45 journaux. Semaine un : 42 journaux. Semaine 2 : 39 journaux. Semaine 3 : 36 journaux. Semaine 4 : 33 journaux. Semaine 5 : 30 journaux. Semaine 6 : 27 journaux. Semaine 7 : 24 journaux. Des flèches représentent les bonds de moins 3 pour les journaux.
b) Combien de temps le camelot prend-il pour livrer tous ses journaux?
J’ai prolongé la table de valeurs jusqu’à ce qu’il reste 0 journal et j’ai constaté que le camelot prend 15 minutes pour livrer tous ses journaux.
| Nombre de minutes écoulées | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Nombre de journaux à livrer | 45 | 42 | 39 | 36 | 33 | 30 | 27 | 24 | 21 | 18 | 15 | 12 | 9 | 6 | 3 | 0 |
Règle de correspondance
Le nombre de journaux livrés est égal au nombre initial de journaux (45) moins trois fois le nombre de minutes écoulées. L’équation est donc j = 45 – 3 m, dont j représente le nombre de journaux à livrer et m, le nombre de minutes écoulées.
Exemple 3
Émilie garde régulièrement des enfants. Un couple lui demande de garder leur enfant 6 heures par jour pendant 10 jours et lui offre de la payer selon la table de valeurs suivante.
| Rang (jour) | 1 | 2 | 3 | 4 | … |
|---|---|---|---|---|---|
| Salaire pour la journée ($) | 1 | 2 | 4 | 8 | … |
Si elle accepte l’offre, combien d’argent Émilie gagnera-t-elle en tout?
Règle de régularité (multiplication)
J’ai remarqué que le salaire double chaque jour. J’ai prolongé la table de valeurs jusqu’à 10 jours. J’ai ensuite additionné les salaires et j’ai trouvé qu’Émilie gagnerait au total 1 023 $ pour 10 jours de gardiennage.
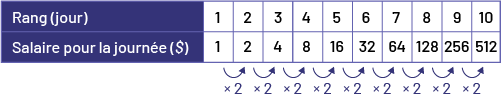 Image Table de valeurs représentant le rang en jour et le salaire pour la journée en dollars. Rang un : un dollar. Rang 2 :2 dollars. Rang 3 : 4 dollars. Rang 4 : 8 dollars. Rang 5 : 16 dollars. Rang 6 : 32 dollars. Rang 7 : 64 dollars. Rang 8 : 128 dollars. Rang 9 : 256 dollars. Rang dix : 512 dollars. Des flèches représentent les bonds de fois 2 des dollars.
Image Table de valeurs représentant le rang en jour et le salaire pour la journée en dollars. Rang un : un dollar. Rang 2 :2 dollars. Rang 3 : 4 dollars. Rang 4 : 8 dollars. Rang 5 : 16 dollars. Rang 6 : 32 dollars. Rang 7 : 64 dollars. Rang 8 : 128 dollars. Rang 9 : 256 dollars. Rang dix : 512 dollars. Des flèches représentent les bonds de fois 2 des dollars.
Exemple 4
À l’occasion d’un tournoi de soccer, 64 équipes sont présentes. Le premier jour, toutes les équipes jouent un match, et les équipes perdantes sont éliminées. Le deuxième jour, les 32 équipes qui restent jouent un match, et les équipes perdantes sont éliminées. Il en est de même chaque jour qui suit.
a) Construis une table de valeurs qui représente la relation entre le rang (jour) et le nombre d’équipes qui jouent un match ce jour-là.
Règle de régularité (division)
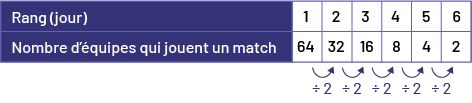 Image Table de valeurs qui représente le rang en jour et le nombre d’équipes qui jouent un match. Rang un : 64 équipes. Rang 2 : 32 équipes. Rang 3 : 16 équipes. Rang 4 : 8 équipes. Rang 5 : 4 équipes. Rang 6 : 2 équipes. Des flèches représentent les bonds de diviser par 2.
Image Table de valeurs qui représente le rang en jour et le nombre d’équipes qui jouent un match. Rang un : 64 équipes. Rang 2 : 32 équipes. Rang 3 : 16 équipes. Rang 4 : 8 équipes. Rang 5 : 4 équipes. Rang 6 : 2 équipes. Des flèches représentent les bonds de diviser par 2.
b) Quel jour aura lieu le dernier match?
Le dernier match aura lieu au cours de la 6e journée.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 35-37.
Il est important de reconnaître que le cheminement vers l’expression d’une équation peut différer d’une ou d’un élève à l’autre, puisque le raisonnement se développe en partant de perceptions individuelles. Le personnel enseignant doit tenir compte des différentes façons qu’ont les élèves de percevoir les relations entre les termes d’une suite et adapter son questionnement en conséquence afin d’aider chaque élève à exprimer la règle en mots avec précision et à déterminer l’équation qui lui correspond.
L’exemple ci-dessous illustre la façon dont les élèves peuvent percevoir différemment la relation entre le rang de la figure dans une suite non numérique croissante et le nombre de carrés qui la composent. La situation met en évidence des exemples de questionnement adapté.
Exemple
Le personnel enseignant présente la suite de figures suivante :
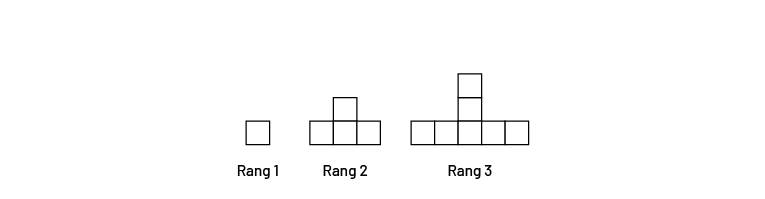
À l’aide des questions ci-dessous, inciter les élèves à analyser la suite et à établir une relation entre le rang de la figure et le nombre de carrés qui la composent :
- Combien de carrés composent le terme de la suite au 1er, au 2e et au 3e rang?
- Combien de carrés faut-il pour construire le terme de la suite au 4e rang? Construisez cette figure.
- Combien de carrés faut-il pour construire le terme de la suite au 5e rang? Construisez cette figure.

- Quelle règle de correspondance voyez-vous dans le nombre de carrés d’un rang à l’autre?
- Construisez une table de valeurs qui représente la relation entre le rang de la figure et le nombre de carrés qui la composent. Quelle régularité voyez-vous dans la table de valeurs?
- Combien y aura-t-il de carrés au 6e rang? au 10e rang? Comment le savez-vous?
- Y a-t-il d’autres façons de le déterminer?
Le personnel enseignant anime ensuite un échange mathématique qui met l’accent sur les différentes perceptions qu’ont les élèves de la relation. Il pose des questions telles que celles présentées ci-dessous afin d’amener les élèves à expliquer leur stratégie et leur règle, puis à les verbaliser.
- Avez-vous trouvé une méthode rapide pour compter le nombre de carrés de la figure située au 4e rang? Pouvez-vous nous l’expliquer?
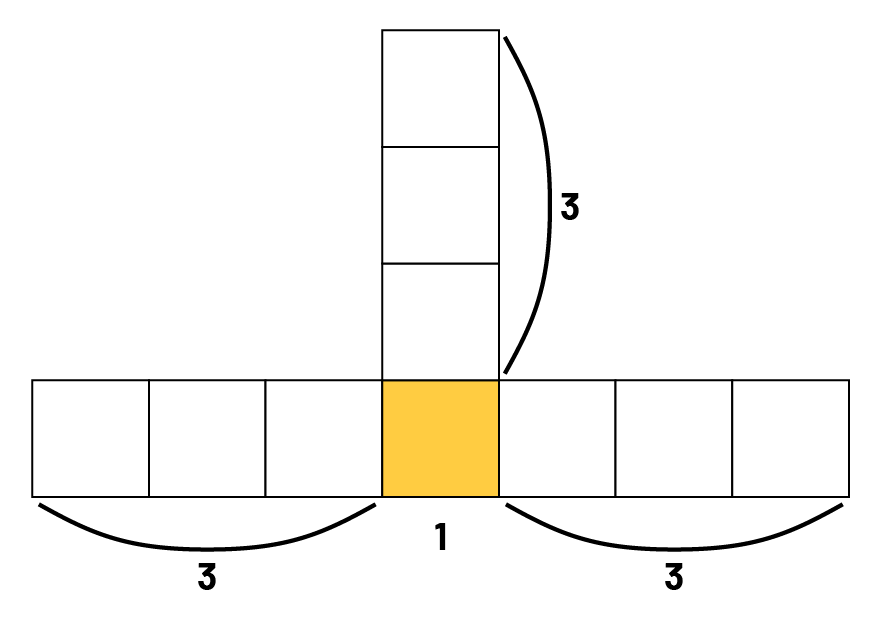
Élève 1 : Dans la figure au 4e rang, je vois qu’il y a 3 carrés à gauche, 3 carrés à droite, 3 carrés en haut et 1 au milieu, en bas. En tout, ça fait 3 + 3 + 3 + 1, soit 10 carrés.
- Qui a utilisé la même méthode? Y a-t-il quelqu’un qui a utilisé une autre méthode?

Élève 2 : J’ai utilisé une méthode semblable. Je vois 1 carré au milieu, en bas, et 3 branches de 3 carrés. En tout, ça fait 1 + (3 × 3), soit 10 carrés.
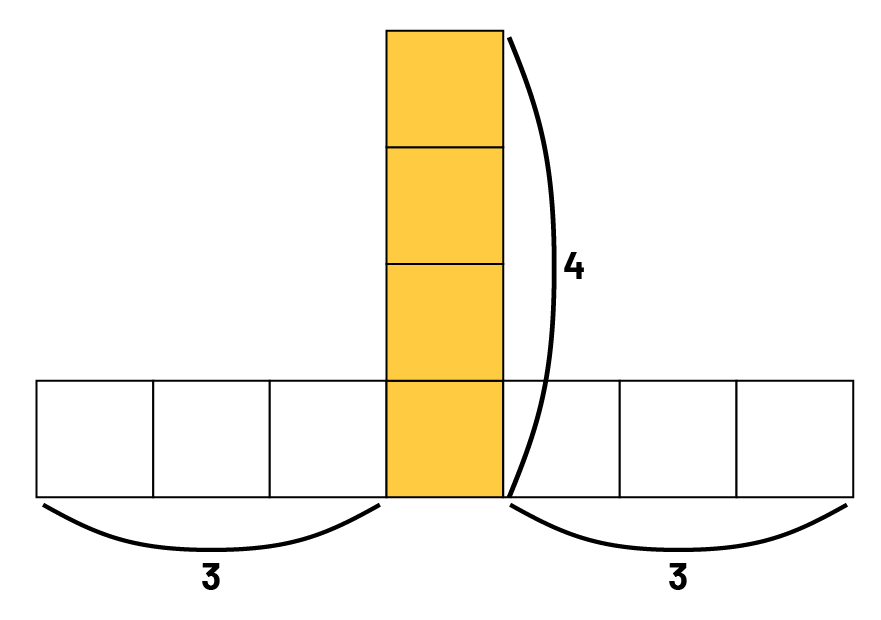 Image Figure
composée de dix carrés. 7 carrés forment la partie horizontale, et 3 carrés sont sur le carré du milieu et font de
façon verticale, cela fait un groupe de 4 carrés. Les carrés restants sont en groupe de 3.
Image Figure
composée de dix carrés. 7 carrés forment la partie horizontale, et 3 carrés sont sur le carré du milieu et font de
façon verticale, cela fait un groupe de 4 carrés. Les carrés restants sont en groupe de 3.
Élève 3 : Moi, ma méthode est différente, mais j’ai obtenu la même réponse. Je vois une colonne de 4 carrés, puis 3 carrés à gauche et 3 carrés à droite. En tout, je compte 4 + 3 + 3, soit 10 carrés.
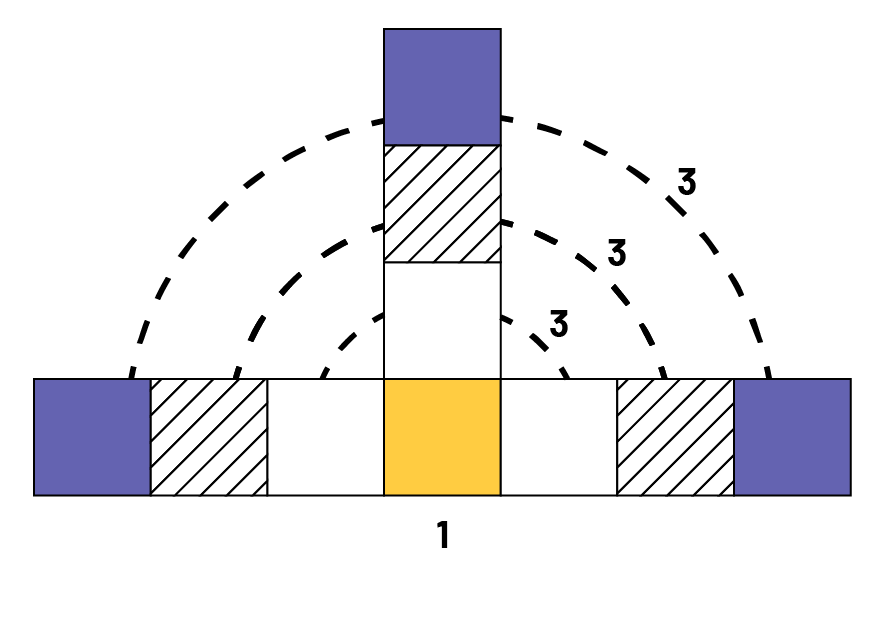 Image Figure
composée de dix carrés. 7 carrés forment la partie horizontale, et 3 carrés sont sur le carré du milieu. Ce carré est
le carré « un ». Des pointillés font un arc de cercle de 3 sur chaque rangée de carrés.
Image Figure
composée de dix carrés. 7 carrés forment la partie horizontale, et 3 carrés sont sur le carré du milieu. Ce carré est
le carré « un ». Des pointillés font un arc de cercle de 3 sur chaque rangée de carrés.
Élève 4 : Moi, je vois les figures d’une autre façon. Si je regarde la suite, elle commence par un carré et, à chaque rang suivant, on ajoute un carré à 3 endroits. Dans la figure située au 4e rang, on a ajouté les 3 carrés 3 fois. En tout, on a 1 + (3 × 3), soit 10 carrés.
- Votre méthode fonctionne-t-elle pour compter le nombre de carrés de la figure située au 5e rang?
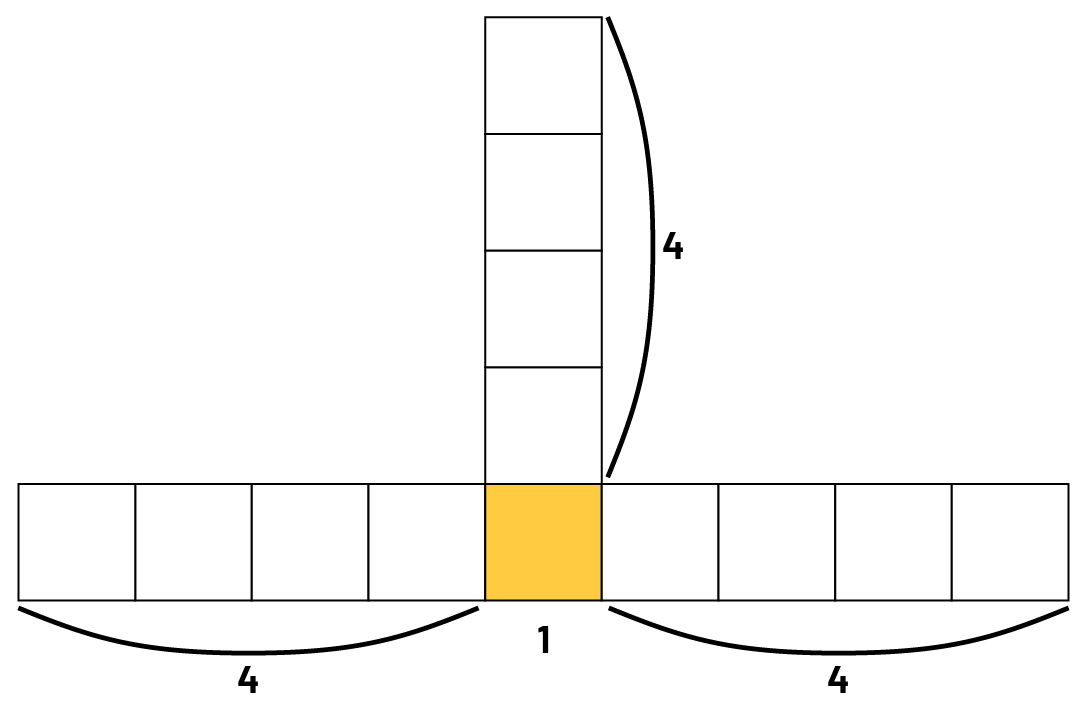
Élève 1 : Oui. Je vois qu’il y a 4 carrés à gauche, 4 carrés à droite, 4 carrés vers le haut et un carré au milieu, en bas. En tout, ça fait 4 + 4 + 4 + 1, soit 13 carrés.
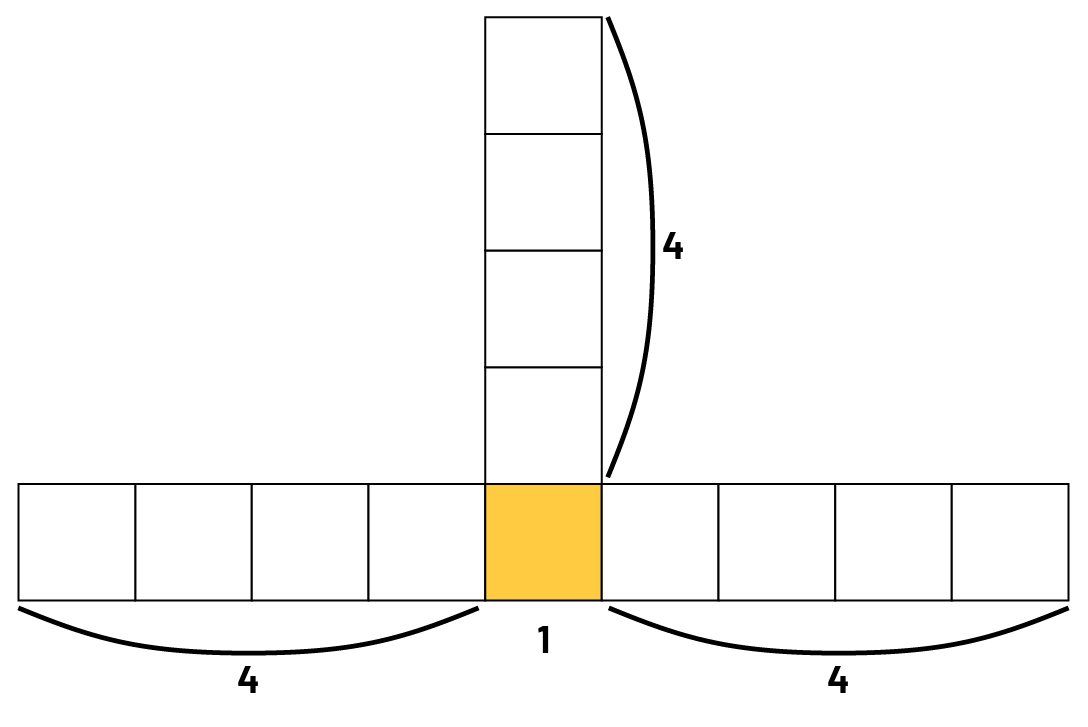
Élève 2 : Oui. Je vois 1 carré au milieu, en bas, et 3 branches de 4 carrés. En tout, ça fait 1 + (3 × 4), soit 13 carrés.
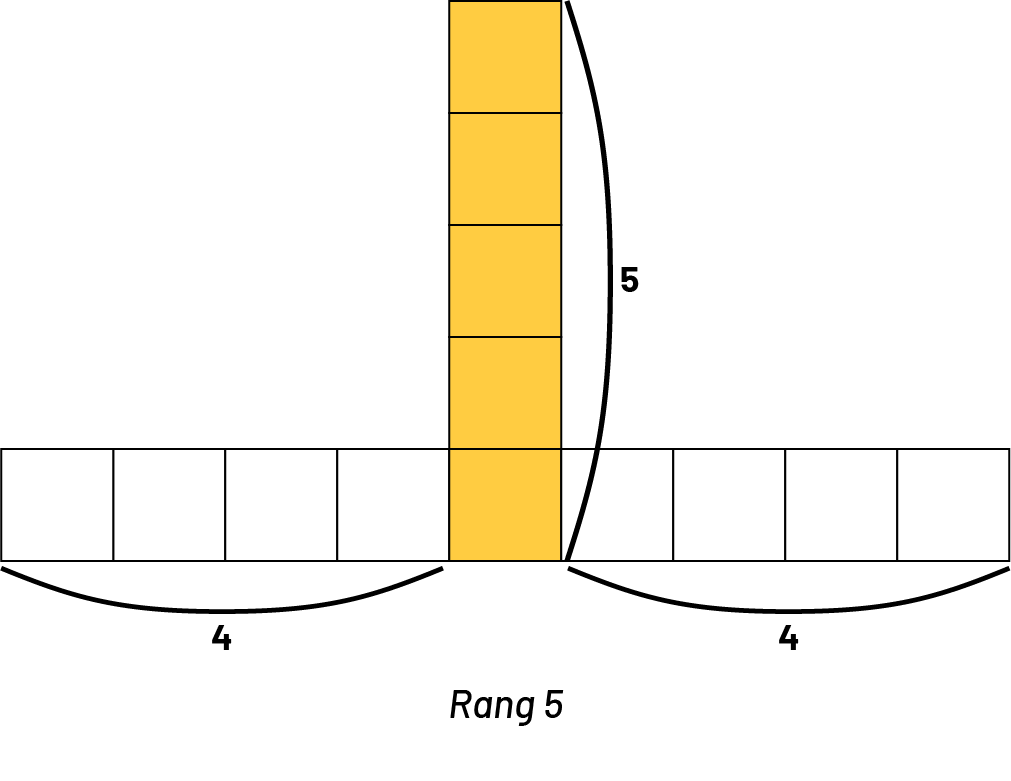 Image Figure
composée de dix carrés. 9 carrés forment la partie horizontale, et 4 carrés sont sur le carré du milieu et font de
façon verticale, cela fait un groupe .de 5 carrés. Les carrés restants sont en groupe de 4
Image Figure
composée de dix carrés. 9 carrés forment la partie horizontale, et 4 carrés sont sur le carré du milieu et font de
façon verticale, cela fait un groupe .de 5 carrés. Les carrés restants sont en groupe de 4
Élève 3 : Oui. Je vois une colonne de 5 carrés, puis 4 carrés à gauche et 4 carrés à droite. En tout, je compte 5 + 4 + 4, soit 13 carrés.
 Image Figure
composée de dix carrés. 9 carrés forment la partie horizontale, et 4 carrés sont sur le carré du milieu. Ce carré est
le carré « un ». Des pointillés font un arc de cercle de 3 sur chaque rangée de carrés.
Image Figure
composée de dix carrés. 9 carrés forment la partie horizontale, et 4 carrés sont sur le carré du milieu. Ce carré est
le carré « un ». Des pointillés font un arc de cercle de 3 sur chaque rangée de carrés.
Élève 4 : Oui. Si je regarde la suite, elle commence par un carré et, à chaque rang suivant, on ajoute un carré à 3 endroits. Dans la figure située au 5e rang, on a ajouté les 3 carrés 4 fois. En tout, on a 1 + (4 × 3), soit 13 carrés.
- Selon votre méthode, combien de carrés y aura-t-il dans la figure située au 10e rang?
Élève 1 : Il y aura 28 carrés. Il y aura 1 carré au milieu, en bas, puis 9 carrés à gauche, 9 carrés à droite et 9 carrés en haut. En tout, il y aura 9 + 9 + 9 + 1, soit 28 carrés.
- Comment sais-tu combien il y en aura à gauche? à droite? en haut?
D’après les premières figures de la suite, il y a toujours 1 carré de moins que le rang de la figure à chacun de ces trois endroits.
Élève 2: C’est presque la même chose.
- Pourquoi dis-tu que c’est la même chose que l’autre stratégie (élève 1)?
L’élève 1 mentionne qu’elle ou il additionne 9 + 9 + 9. Moi, je dis que je multiplie, c’est-à-dire que je fais 3 × 9, car multiplier, c’est comme additionner plusieurs fois une même quantité.
Élève 3: Moi, j’ai aussi obtenu 28, puisqu’il y aura une colonne de 10 carrés, puis 9 carrés à gauche et 9 carrés à droite, donc 10 + 9 + 9 = 28 carrés.
- Comment sais-tu que c’est bien 10 carrés, puis 9 carrés deux fois?
D’après les premières figures de la suite, le nombre de carrés dans la colonne est égal au rang de la figure et le nombre de carrés à gauche et à droite est toujours 1 de moins que ce rang.
Élève 4 : D’après ma façon de voir les figures, il y aura 1 carré au milieu, en bas. Ensuite, on ajoute chaque fois 3 carrés pour passer au rang suivant. On doit le faire pour les figures situées au rang 2 jusqu’au rang 10, soit 9 fois. En tout, on aura alors 1 + (9 × 3), ou 28 carrés.
Note : On remarque que les calculs effectués sont similaires. Cependant, les différentes façons de voir l’organisation des carrés dans la figure et l’expression de cette organisation ont généré des règles différentes, mais équivalentes.
- Votre méthode rapide pour compter (votre règle) peut-elle être utilisée pour déterminer le nombre de carrés qu’il y aura dans la figure au 25e rang?
Lorsque les élèves expliquent, en mots, la façon de déterminer la valeur d’une figure d’un rang éloigné, comme la figure au 10e ou au 25e rang, en relation avec le rang d’une figure, elles et ils utilisent leur règle pour interpréter la relation.
Pour aider les élèves ayant souvent de la difficulté à déterminer les quantités en jeu, le personnel enseignant pose des questions telles que celles présentées ci-dessous afin de les amener à exprimer leur règle plus clairement et à exprimer la relation à l’aide d’une équation.
- Comment pouvez-vous déterminer le nombre de carrés qui composent n’importe quelle figure?
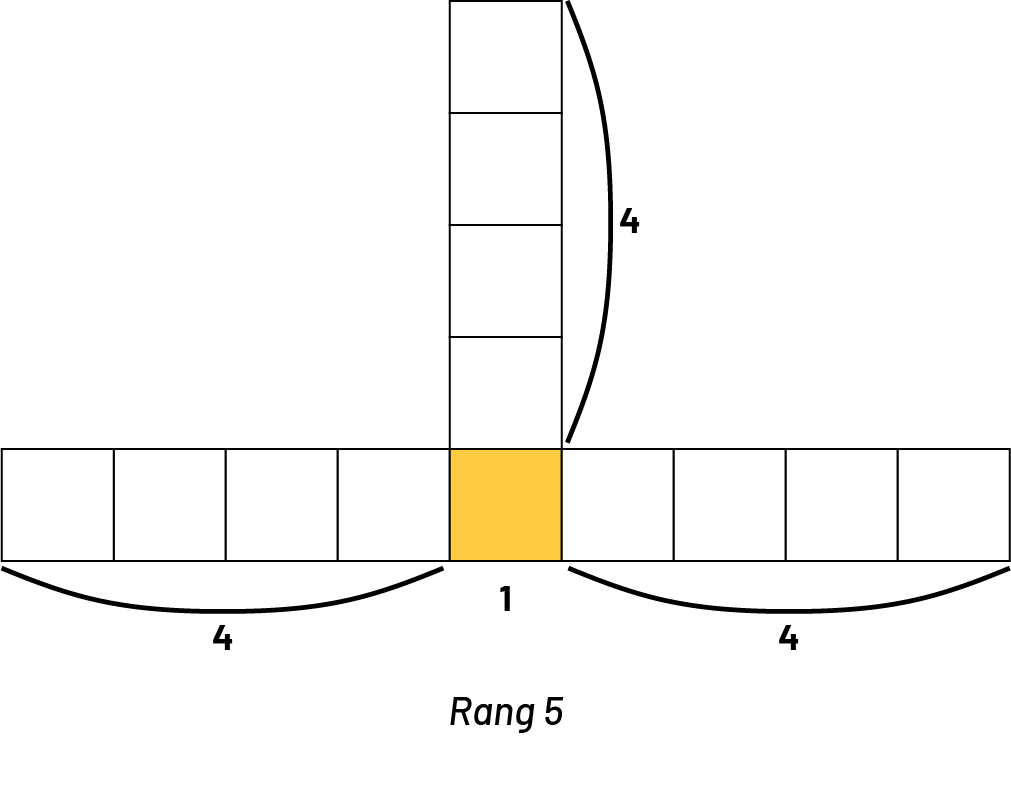
Élève 1 : Pour déterminer le nombre de carrés qui composent n’importe quelle figure, j’additionne un nombre 3 fois, puis 1.
- Quel est ce nombre? Comment peux-tu le nommer?
C’est toujours le rang de la figure précédente.
- Peux-tu alors exprimer ta règle de correspondance pour déterminer le nombre de carrés qui composent n’importe quelle figure avec plus de précision?
Pour déterminer le nombre de carrés qui composent n’importe quelle figure, j’additionne le rang de la figure précédente 3 fois, puis 1.
- Peux-tu maintenant exprimer cette règle de correspondance à l’aide d’une représentation symbolique?
L’équation serait c = (r − 1) + (r − 1) + (r − 1) + 1, où r représente le rang de la figure et c, le nombre de carrés qui la composent.
Élève 2 : Pour déterminer la valeur de n’importe quel terme, je multiplie par 3 et j’ajoute 1.
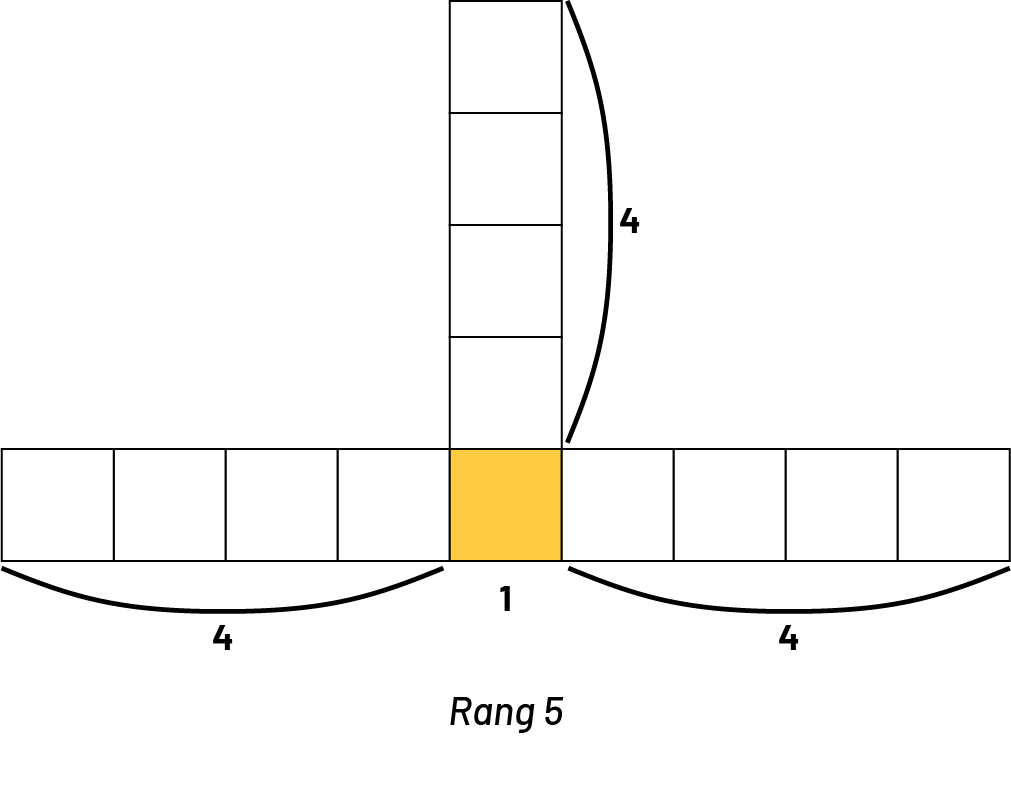
- Qu’est-ce que tu multiplies par 3? Que détermines-tu?
Je multiplie le rang de la figure précédente par 3 et j’ajoute 1. Cela me donne le nombre de carrés qui composent la figure en question.
- Si l’on représente le rang de la figure par r, comment peut-on représenter le rang de la figure précédente?
Il s’agit de r − 1. Donc, l’équation est c = 1 + 3 × (r − 1), où r représente le rang de la figure et c, le nombre de carrés qui la composent.
Élève 3 : Dans chaque figure, il y a toujours 3 branches. Une branche qui a le même nombre de carrés que le rang de la figure et deux autres qui ont 1 carré de moins que le rang de la figure. Pour déterminer le nombre de carrés, j’additionne ces trois nombres.
 Image Figure
composée de dix carrés. 9 carrés forment la partie horizontale, et 4 carrés sont sur le carré du milieu et font de
façon verticale, cela fait un groupe de 5 carrés. Les carrés restants sont en groupe de 4.
Image Figure
composée de dix carrés. 9 carrés forment la partie horizontale, et 4 carrés sont sur le carré du milieu et font de
façon verticale, cela fait un groupe de 5 carrés. Les carrés restants sont en groupe de 4.
- Peux-tu m’expliquer cette règle de façon plus concise?
Pour déterminer le nombre de carrés qui composent une figure quelconque, j’additionne 3 valeurs, soit le rang de la figure et deux fois le rang de la figure précédente. Donc, c = r + (r − 1) + (r − 1), où r représente le rang de la figure et c, le nombre de carrés qui la composent.
Élève 4 : Je fais 3 fois un nombre pour déterminer le nombre de carrés sur les 3 branches et j’ajoute 1 pour celui qui est au centre. En fait, je multiplie le rang de la figure précédente par 3 et j’ajoute 1. Donc, c = (r − 1) × 3 + 1, où r est le rang de la figure et c, le nombre de carrés qui la composent.
 Image Figure
composée de dix carrés. 9 carrés forment la partie horizontale, et 4 carrés sont sur le carré du milieu et font de
façon verticale, cela fait un groupe de 5 carrés. Les carrés restants sont en groupe de 4.
Image Figure
composée de dix carrés. 9 carrés forment la partie horizontale, et 4 carrés sont sur le carré du milieu et font de
façon verticale, cela fait un groupe de 5 carrés. Les carrés restants sont en groupe de 4.
Le personnel enseignant invite ensuite les élèves à vérifier la validité de leur équation. Pour valider les équations, on utilise la table de valeurs.
- D’après votre règle, si r prend une valeur de 4, quelle est la valeur correspondante de c?
Élève 1 : Mon équation devient c = (4 – 1) + (4 – 1) + (4 – 1) + 1. Donc, c = 10.
Élève 2 : Mon équation devient c = 1 + 3 × (4 – 1). Donc, c = 10.
Élève 3 : Mon équation devient c = 4 + (4 – 1) + (4 – 1). Donc, c = 10.
Élève 4 : Mon équation devient c = (4 – 1) × 3 + 1. Donc, c = 10.
- À quoi correspond cette valeur de c dans votre équation?
Élève 1 : La variable c représente le nombre de carrés qui composent la figure. Dans la suite donnée, il est vrai que la figure située au 4e rang est composée de 10 carrés.
- D’après votre équation, c = 10 lorsque r = 4. À quoi cela correspond-il dans la table de valeurs?
Élève 2 : Selon la table de valeurs, la figure au 4e rang est composée de 10 carrés. Cela correspond à ce que j’obtiens avec l’équation.
L’exemple précédent suit une certaine démarche qui peut être résumée comme suit : demander aux élèves de prolonger la suite de figures, d’analyser la règle et de la décrire, de construire une table de valeurs, puis de formuler une règle en mots et à l’aide d’une représentation symbolique. Cette démarche encourage l’exploration de toutes sortes de relations, même certaines qui peuvent d’abord sembler être hors de la portée des élèves. Cette démarche est utilisée pour des suites croissantes et décroissantes.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 54-64.
Habileté : utiliser les représentations symboliques des règles pour trouver des valeurs inconnues dans des suites croissantes linéaires
Parmi les représentations symboliques des suites croissantes, les règles sous forme d’équations aident plus facilement et plus précisément à faire des interpolations et des extrapolations que les représentations graphiques.
Pour établir ces règles, il est important d’aider les élèves à généraliser, c’est-à-dire :
- les guider dans l’observation et l’analyse des situations;
- les aider à proposer des conjectures;
- leur demander d’appuyer leurs conjectures à l’aide de représentations mathématiques ou d’arguments mathématiques;
- les inviter à vérifier leurs conjectures dans d’autres situations;
- les accompagner dans la formulation d’une généralisation, s’il y a lieu.
Source : Guide d’enseignement efficace des mathématiques de la 7e à la 10e année, p. 12.
Dans cette vidéo, on apprend comment une équation est utilisée pour modéliser une situation de la vie quotidienne.
 Description de la vidéo
Description de la vidéo
Description à venir
Exemple de représentation de la relation entre deux quantités changeantes
Écrire l’équation c = i × 2 au tableau et présenter son contexte :
Éric invite des amis chez lui. Lorsqu’ils entrent, il leur demande d’enlever leurs chaussures et de les mettre sur une marche de l’escalier. On s’intéresse à la relation entre le nombre d’invités (i) et le nombre de chaussures (c).
Avec les élèves, construire une table de valeurs représentant la relation ainsi qu’une suite non numérique.
| Nombre d'invités (i) | 1 | 2 | 3 | ... |
|---|---|---|---|---|
| Nombre de chaussures (c) | 2 | 4 | 6 | ... |
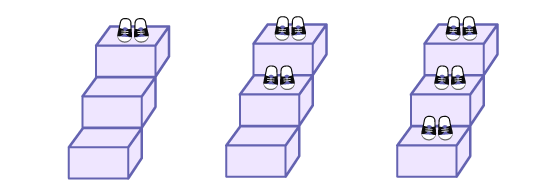 Image Suite
non numérique à motifs croissants. Sur un escalier de 3 marches, il y a une paire de souliers. Sur un escalier de 3
marches, il y a 2 paires de souliers. Sur un escalier de 3 marches, il y a 3 paires de souliers.
Image Suite
non numérique à motifs croissants. Sur un escalier de 3 marches, il y a une paire de souliers. Sur un escalier de 3
marches, il y a 2 paires de souliers. Sur un escalier de 3 marches, il y a 3 paires de souliers.
Demander aux élèves d’expliquer ce que représentent la variable i (le nombre d’invités), la variable c (le nombre de chaussures) et le « × 2 » (le nombre de chaussures par personne).
Questions pertinentes :
- Comment pouvez-vous représenter cette situation à l’aide d’un autre modèle?
- Quelle est la règle de correspondance dans la suite? Que représente-t-elle?
- Comment avez-vous trouvé le nombre total de chaussures dans la table de valeurs?
- Combien de chaussures se retrouveront dans l’escalier si Éric invite 6 amis?
- Combien de souliers y aura-t-il lorsque le 15e invité se déchaussera?
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 238.
Connaissance : interpolation
Opération qui consiste à estimer la valeur d’une variable entre deux valeurs connues.
Source : Curriculum de l’Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l’Éducation de l’Ontario.
Exemple
Trouver la valeur du coût lorsque la quantité est 7.
| Quantité | 2 | 4 | 6 | 8 | 10 | 12 |
|---|---|---|---|---|---|---|
| Coût | 6 | 12 | 18 | 24 | 30 | 36 |
Note : Dans ce cas, l’élève peut faire la moyenne entre les coûts pour 6 et 8.
Connaissance : extrapolation
Opération qui consiste à estimer la valeur d’une variable à partir de données à l’extérieur de l’intervalle observé.
Source : Curriculum de l’Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l’Éducation de l’Ontario.
Exemple
Trouver la valeur du coût si la quantité est 22.
| Quantité | 2 | 4 | 6 | 8 | 10 | 12 |
|---|---|---|---|---|---|---|
| Coût | 6 | 12 | 18 | 24 | 30 | 36 |
Note : Dans ce cas, l’élève peut d’abord déterminer que l’équation est c = 3q, puis calculer le coût en remplaçant q par 22, ce qui donne 66 $.
Note : Afin d’éviter la mémorisation de démarches et de provoquer la construction du sens, varier la valeur inconnue recherchée. Cela provoquera une flexibilité cognitive et un questionnement relativement au concept exploré.
