C1.2 Créer des suites à motif répété, des suites croissantes et des suites décroissantes comprenant des nombres naturels et des nombres décimaux à l’aide d’une variété de représentations, y compris des expressions algébriques et des équations pour des suites croissantes linéaires, et établir des liens entre les différentes représentations.
Activité 1 : les stratégies (suites croissantes linéaires)
Découper les équations, les tables de valeurs et les représentations graphiques du tableau ci-dessous. Diviser les élèves en équipes et distribuer les formes de représentations découpées à chacune des équipes. Les équipes doivent associer les différentes représentations de suites linéaires de façon à regrouper la représentation graphique, la table de valeurs et l’équation en comparant les valeurs initiales, b, et le taux constant, m (par exemple, 1A, 2B et 3C pourraient représenter la même situation).
Faire un retour en groupe-classe en mettant l’accent sur la ou les stratégies de regroupement des élèves.
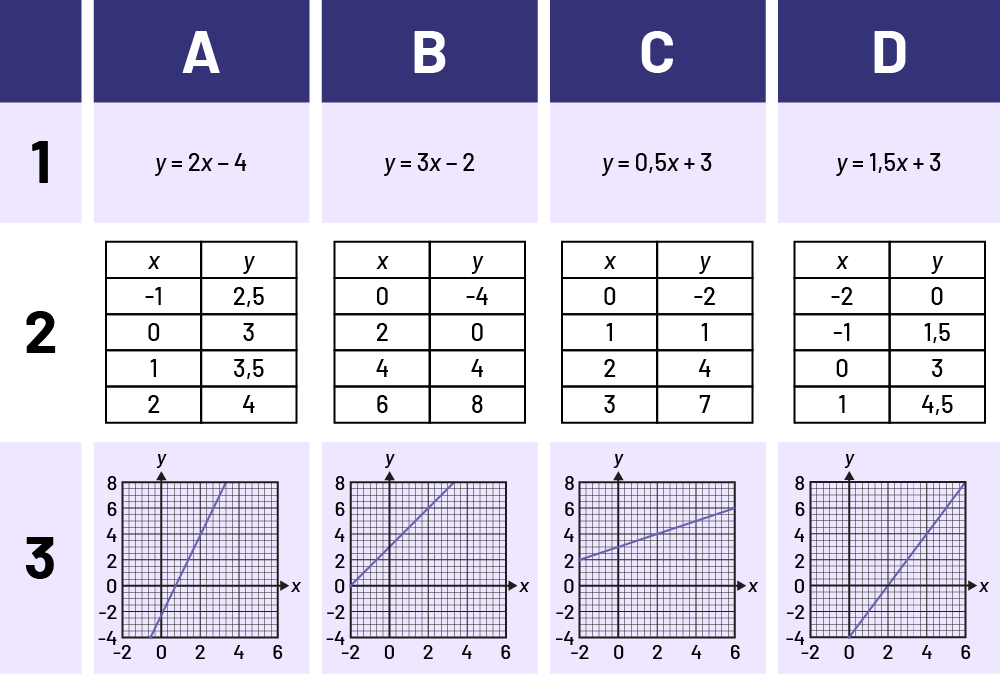
Stratégie 1 : Solution déterminée en comparant les valeurs initiales dans les 3 formes de représentations des situations linéaires
Je cherche dans l’équation la valeur du terme individuel (le b dans la formule \( y = mx +b\)). Dans la table de valeurs, je cherche la valeur de y quand x = 0. Dans le graphique, je cherche la valeur de y quand la suite linéaire croise l’axe des ordonnées (y).
Première situation : La droite linéaire croise l’axe des ordonnées à \(y = -4\).
Solution : A1, B2, D3
Deuxième situation : La droite linéaire croise l’axe des ordonnées à \(y = -2\).
Solution : B1, C2, A3
Troisième et quatrième situations, C1 et D1 : Je rencontre un problème, car il y a 2 possibilités lorsque je trouve la valeur y lorsque x = 0, soit C1 (b = 3) et D1 (b = 3). Je ne peux pas aller plus loin en utilisant cette stratégie.
Stratégie 2 : Solution déterminée en comparant les taux constants dans les 3 formes de représentations des situations linéaires
Je vais regarder les taux constants dans les équations, les bonds dans les tableaux de valeurs et l’inclinaison des droites dans les graphiques.
Première situation : A1 a un taux constant de 2 dans l’équation, ce qui implique une droite linéaire croissante inclinée dans le graphique D3. Cela implique, pour chaque valeur en x, des bonds de 2 aux valeurs de y dans la table de valeurs B2.
Solution : A1, B2, D3
Deuxième situation : B1 a un taux constant de 3 dans l’équation, ce qui implique une droite linéaire croissante très inclinée dans le graphique A3. Cela implique, pour chaque valeur en x, des bonds de 3 aux valeurs de y dans la table de valeurs C2.
Solution : A3, B1, C2
Troisième situation : C1 a un taux constant de 0,5 dans l’équation, ce qui implique une droite linéaire qui grimpe lentement dans le graphique C3. Cela implique, pour chaque valeur en x, des bonds de 0,5 aux valeurs de y dans la table de valeurs A2.
Solution : C1, A2, C3
Quatrième situation : D1 a un taux constant de 1,5 dans l’équation, ce qui implique une droite linéaire qui grimpe assez rapidement dans le graphique B3. Cela implique, pour chaque valeur en x, des bonds de 1,5 aux valeurs de y dans la table de valeurs D2.
Solution : D1, D2, B3
Source : En avant, les maths!, 7e année, CM, Algèbre, p. 5-7.
Activité 2 : création d’une suite linéaire
Matériel :
- cubes emboîtables;
- papier quadrillé;
- blocs ou objets quelconques.
Préparer 5 stations avec du matériel de manipulation. À chaque station, les élèves devront créer une suite croissante linéaire avec le matériel. Une fois terminée, elles et ils devront créer une table de valeurs, faire la représentation graphique et établir l’équation la définissant. Allouer une quinzaine de minutes par station. Prendre des photos et les utiliser pour faire un retour en groupe-classe. Discuter des stratégies, du vocabulaire et des différentes représentations (matériel, table de valeurs, graphiques et équations).
Note : Pour chaque suite, les élèves devraient être en mesure de relever la valeur initiale (rang 0) et le taux de variation constant. Au besoin, guider les élèves.
