General Foundations of Algebra
Intermediate Division
Introduction
The study of algebra was developed from the need to understand the real world and to represent it in order to solve problems. Over the centuries, mathematicians have attempted to solve problems by observing patterns and representing phenomena (for example, determining the diameter of the Earth, predicting the movement of tides, explaining the motion of falling objects). Their work contributed to the development of mathematical symbols and methods of calculation.
The Ontario Ministry of Education, in Paying Attention to Algebraic Reasoning K-12 (Ontario Ministry of Education, 2013), argues that 'algebraic reasoning underpins all mathematical thinking, including arithmetic, because it allows us to explore the structure of mathematics. We now recognize the importance of including algebraic reasoning in mathematics instruction from a very young age so that powerful mathematical ideas are accessible to all students.
Everyone has the capacity to think algebraically because algebraic reasoning is essentially the way humans interact with the world. We look for patterns, pay attention to aspects of the pattern that are important, and then generalize from familiar to unfamiliar situations.' (p. 3)
It is by addressing concrete situations that students consolidate their understanding of the representations of a situation (words, terms of a growing pattern, graphical representation, table of values and equations) and formalize mathematical ideas using algebraic symbols (variables).
Algebraic Reasoning
Algebraic reasoning moves a student's understanding of mathematics beyond the results of calculations and the procedural application of formulas. However, unlike natural number learning, the development of algebraic reasoning requires the learner to think beyond arithmetic. The acquisition of this form of reasoning is progressive. It evolves with the student's experience in exploring situations that can be generalized.
While considering the elements specific to the development of algebraic reasoning, teachers must incorporate the essential elements of effective mathematics instruction, including communication and problem-solving skills, into their instruction.
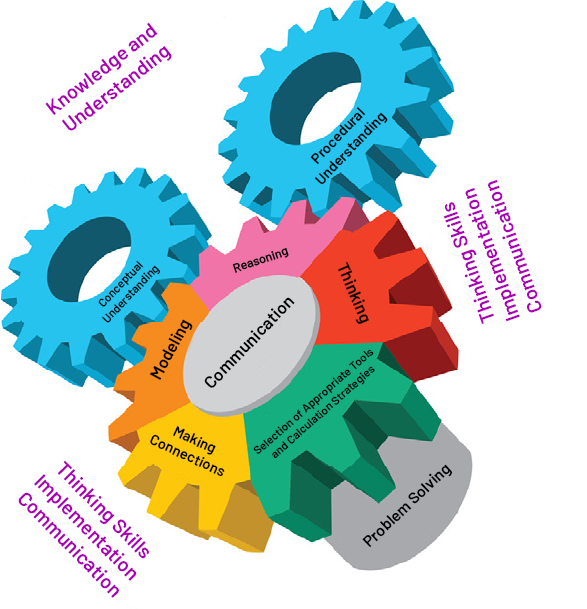image Infographic. A gear wheel is placed on an axis named 'problem solving'. The gear, which is on this axis, is divided into 5 parts: thinking; selecting appropriate tools and computational strategies; making connections; modeling; and reasoning. All revolving around communication. These five elements allow for: thinking skills, application and communication. On the gears, modelling and reasoning, there is another wheel of conceptual understanding, and a wheel of procedural understanding. This will bring knowledge and understanding.
Source: translated from Guide d’enseignement efficace des mathématiques de la 7e à la 10e année, p. 6-9.
In the intermediate grades, algebraic reasoning evolves by using abstraction in increasingly complex situations and by practicing generalization and operation on variables. These three processes of algebraic reasoning are 'interactive' and not 'hierarchical'. They facilitate problem solving and lead the student to think algebraically.
Abstracting
Abstracting is one of the fundamental processes of algebraic reasoning. 'To abstract is to detach oneself from the sensory aspect of things in order to reason at a more general level (adapted from Raynal and Rieunier, 2003, p. 13), it is to mentally represent a concrete situation, it is to move to a deeper level of conceptualization.' (Ontario Ministry of Education, 2008a, p. 9)
Example
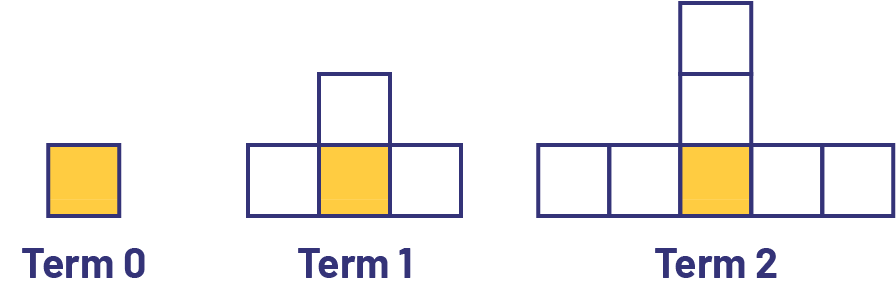image An example of abstract algebraic reasoning about squares. zero: a yellow square. one: one yellow square and one white square on top, right and left. two: one yellow square, two white squares on top vertically and two white squares on each side.
| Level of Abstraction | Student's Reflection |
|---|---|
| When analyzing the above growing pattern, it is common for the student to give a description of any term rather quickly. The student explains the pattern without representing it concretely: a first abstraction is then developed. Based on particular terms, the student says that they can describe the 10th term and even the 100th term. However, whatever the position of the term, the explanation sometimes remains for a long time anchored in the process of construction of these particular terms. | In position 0, there is a yellow square. In position 1, there is a yellow square and a group of 3 white squares. In position 2 there is one yellow square and 3 groups of 2 white squares. So, in position 3, there will be one yellow square and three groups of white squares. The term in position 3 will have 3 groups of 3 white squares (3 × 3) + one yellow square which makes 10 in all. In position 10, the term will have 10 groups of 3 white squares (10 × 3) + 1 yellow square, which is 31 squares. |
| The student must perform a second abstraction to arrive at '… an algebraic generalization, that is, to a generalization whose variable is expressed by an indeterminate number' (Radford, Demers, & Miranda, 2009, p. 16). The student first expresses the rule in words and then performs a generalization using an equation. | The number of squares in the term is equal to the row number × 3 and then I added 1 to it. Or Using an equation s = 3 × p + 1 (or s = 3p + 1), where s is the number of squares and pthe position number, I describe any term, whatever its position. Note: In this equation which generalizes the rule of the growing pattern, the rule is composed of a multiplier (× 3) and a constant (+ 1). |
It is the teacher's role to develop students' level of abstraction by providing opportunities to make such generalizations using problems of increasing difficulty.
Generalizing
The word conjecture is similar to the word hypothesis used more in the overall and specific expectations of the curriculum; for example, 'to hypothesize about the existence of a relationship between two variables.' (Ontario Ministry of Education, 2005b, p. 30)
Helping students generalize is to:
- guide them in the observation and analysis of situations;
- encourage them to make conjectures;
- ask them to support their conjectures with mathematical representations or arguments;
- invite them to verify their conjectures in other situations;
- support them in the formulation of a generalization, if possible.
Example
Abdel gives the students a rectangle and asks them to determine its area. Then, he asks them to come up with a conjecture about the measurement of the area. 'If the base measurement of the rectangle is doubled, what happens to the area measurement?'
A student offers a conjecture, 'The area will also double.'
To verify the conjecture, the teacher asks students to double the length of the base and determine the area of the new rectangle.
Then the teacher invites the students to analyze the results to determine what happens to the area of a rectangle when the measurement of its base is doubled.
Then, the teacher asks students to check if the conjecture is true for other rectangles.
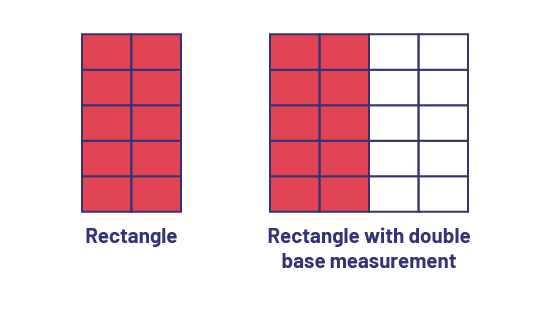
Recognizing that their conjecture seems to apply to all similar situations, students can make a generalization using words or symbols.
Student reasoning: If the length of the base of a rectangle is doubled, the area of the rectangle is also doubled.
If b × h = A, then 2b × h = 2A.
When the development of algebraic reasoning becomes a learning goal, teachers provide students with a variety of explorations so that they can generalize. These different explorations should lead students to make generalizations about the properties of numbers based on the observation of growing patterns, and to discover formulas and generalizations related to measurement and geometry.
Operating on Variables
Operating on variables is the action of analyzing and acting on what is unknown. 'It is reasoning analytically, thinking about operations, generalizations, not objects (adapted from Squalli & Theis, 2005).' (Ontario Ministry of Education, 2008a, p. 11)
Note: We are referring here to unknown quantities in the broad sense of the word and not to the unknown quantity in the sense of a symbol or value that is not known.
It is also to examine the elements of an operation, of a number pattern in order to identify the change. In other words, 'algebraic reasoning … allows one to manipulate any unknown quantity as if it were known.' (Ontario Ministry of Education, 2013, p. 4)
Variables and symbols make it possible to observe and describe the actions taken to solve a problem and to generalize it.
Source: translated from Guide d’enseignement efficace des mathématiques de la 7e à la 10e année, p. 10-13.
Students' algebraic thinking develops in conjunction with the development of mathematical skills. Thus, students need to develop the ability to reason and solve problems algebraically and then communicate their algebraic reasoning.
Ability to Reason Algebraically
While arithmetic is generally perceived as a calculation on known quantities, focusing on finding the right answer, algebraic reasoning aims to better understand numeration through the analysis of relationships between numbers. This is why it is essential for the students to develop the ability to reason algebraically, especially in problem-solving situations.
According to Driscoll (1999, p. 1-19), algebraic reasoning includes the ability to “do and undo”, the ability to create rules to represent relationships between two changing quantities and the ability to formulate generalizations about the properties of arithmetic operations.
The ability to “do and undo” occurs when students succeed in working backwards. For example, students can make use of the connections between addition and subtraction and between multiplication and division. Given the equation Δ + 3 = 11, a student who can work backwards understands that 3 can be subtracted from the sum (11 – 3 = 8) to determine the unknown quantity, since we have added 3 to the variable to get a sum of 11. This is algebraic reasoning, since the action is performed based on thought and understanding, not a procedure for which the student cannot explain its meaning.
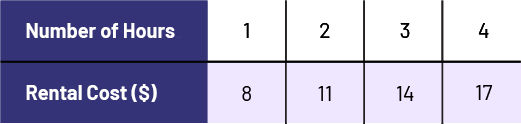
The ability to create rules to represent relationships involves the ability to generalize from rules. For example, in the growing pattern below, the student reasoning algebraically can first recognize that at position 1, the term is composed of 1 column of 2 dots, that at position 2, the term is composed of 2 columns of 3 dots… Thus, the student can generalize and represent the relationship between the number of dots (d) and the position number (p) by an equation [for example, d = p × (p + 1)].
The ability to generalize properties of arithmetic operations also demonstrates algebraic reasoning (for example, knowing that you can change the order of two numbers you want to add without affecting the sum or that the product of a number and 1 is always equal to the number).
Algebraic reasoning is also distinguished from arithmetic reasoning in the following way; Arithmetic reasoning is more concerned with static situations, whereas algebraic reasoning is more concerned with changing situations. Developing students' algebraic reasoning allows them to see and analyze more encompassing situations and to develop their repertoire of problem-solving strategies.
To stimulate students' algebraic reasoning, teachers can use an existing arithmetic problem and give it an algebraic perspective by adding a changing situation. These situations encourage the search for regularities and relationships, the use of variables, and the expression of justifications, conjectures and generalizations.
The table below highlights the difference between a problem that elicits arithmetic reasoning and a problem that elicits algebraic reasoning.
| Arithmetic Reasoning | Algebraic Reasoning |
|---|---|
|
Students work from a static situation. Example This problem presents a static situation. It results a single answer which must be determined using arithmetic operations. |
Students work from a changing situation. Example
This problem presents a changing situation. It focuses on the study of pattern rule and especially of the relationship between two changing quantities. |
Through algebraic reasoning, students analyze numbers, symbols, quantities, operations, and then generalize them.
The ability to reason algebraically does not develop in a simple and natural way. Therefore, teachers need to walk students through the process by encouraging them to:
- explain their reasoning;
- work backwards;
- analyze the relationships between quantities and organize information to represent a situation in another way;
- make conjectures and generalize.
During learning situations teachers should ask questions that emphasize algebraic concepts and encourage students' thinking.
Here are some examples:
- Does it work if I do the same with other numbers?
- What changes? What does not change?
- Can I predict the outcome based on the information gathered?
- Can the regularity be applied to any case?
- Do I always follow the same steps? What are they?
Ability to Solve a Problem Algebraically
Problem solving is designed to engage students in a process that requires the use of different strategies. Students who have developed strategies find it easier to initiate the resolution of a problem, to anticipate and predict outcomes, to reason and to find a solution.
A problem-solving situation refers to a problem that:
- is in context;
- allows the use of different strategies;
- is a challenge for the student.
Here is a problem that can be solved arithmetically or algebraically.
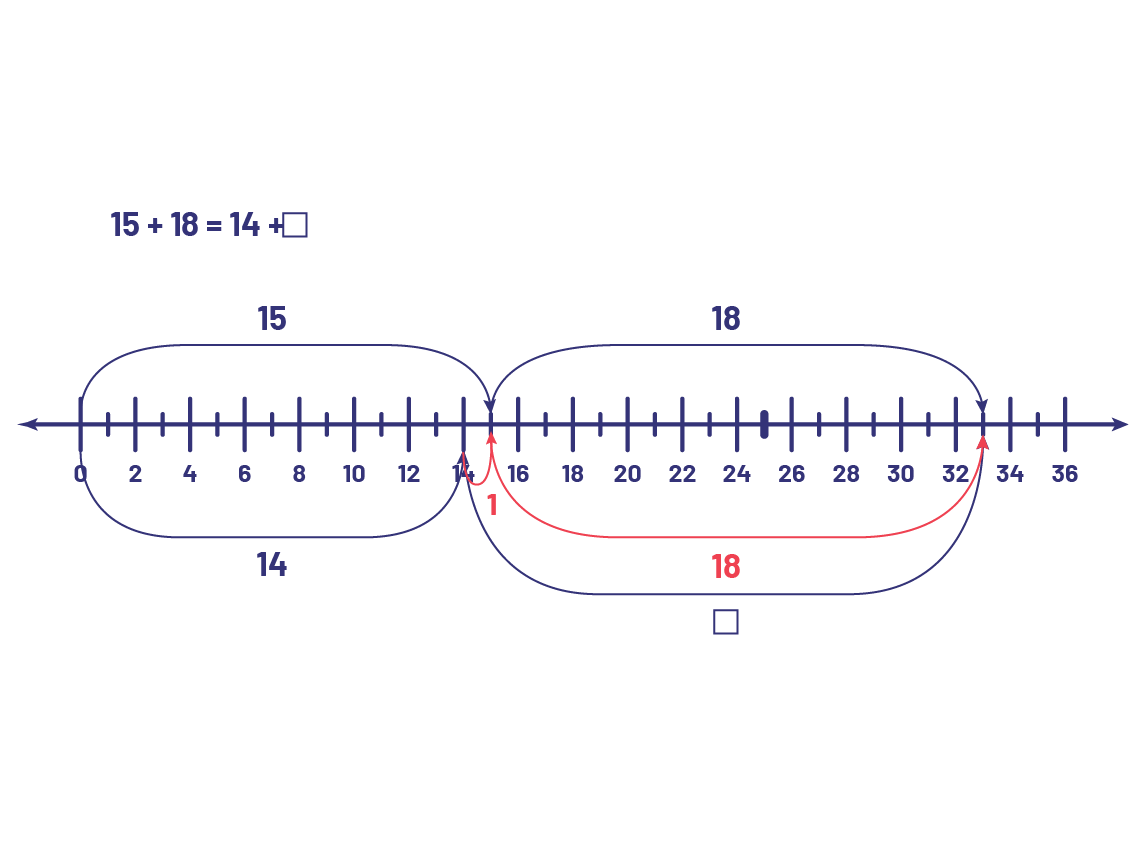
Sylvia has 15 red fish and 18 yellow-striped fish. Jacob has the same number of fish, but only 14 of his fish are red. How many yellow-striped fish does Jacob have?
| Solving with arithmetic reasoning | Solving with algebraic reasoning |
|---|---|
| I know that Sylvia has 33 fish in total, because 15 plus 18 is 33. 15 + 18 = 33 Jacob has the same number of fish. So if he has 14 red fish, he has 19 fish with yellow stripes, because 33 minus 14 is 19. 33 - 14 = 19 We perform arithmetic operations to solve the problem. |
I know that Sylvia and Jacob have the same number of fish. 15 + 18 = 14 + □ If Sylvia has 15 goldfish and Jacob has 14, then Jacob has 1 less goldfish than Sylvia. Since Jacob has the same number of fish as Sylvia, he must have 1 more yellow-striped fish than Sylvia .Therefore □ = 19. Instead of doing calculations, we interpret the problem and compare the quantities. We can represent the situation with an equation. To solve it, we compare the quantities on either side of the '=' sign.  |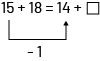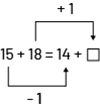
In general, students tend to solve such a problem arithmetically. Teachers can then vary the parameters of the problem by giving it an algebraic perspective, for example, by asking students to represent the problem using an equation. To solve the equation, students can use a number line, which can help them think about the calculation, not do the calculation. The important thing is not to do the calculation, but to understand the relationship of equality between the two numerical expressions.
Ability to Communicate Algebraic Reasoning
Communication benefits everyone involved in the exchange. The obligation to share one's understanding of a situation or concept often contributes to the improvement or deepening of that understanding.
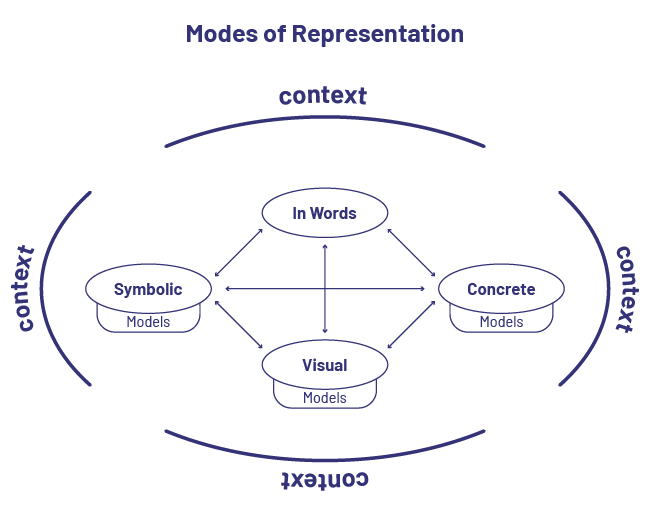
The ability to communicate algebraic reasoning is developed when students express their understanding of a problem or concept and defend their ideas using different representations:
- the concrete mode, linked to exploration, manipulation and creation using concrete materials;
- the semi-concrete mode, linked to an illustration, a drawing or any other representation on paper;
- the symbolic mode, linked to any representation made from numbers or symbols;
- the 'in words' mode, linked to an explanation or a verbal or written description.
Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Algèbre, pp. 12-19.
Students show their understanding of relationships using different representations: relationship in situation (words, terms in a growing pattern), table of values, equation and graphic representation.
It is important for students in grades 7 and 8 to continue to represent a situation using concrete materials, semi-concrete materials and words before moving on to symbolic representation. Analysis of growing patterns helps them develop the ability to translate a situation into an equation. Students achieve algebraic generalization by filling in a table of values, verbally describing terms further down the pattern, and analyzing numerical expressions. It is also important that students associate growing patterns with a story in context.
Source: translated from Guide d’enseignement efficace des mathématiques de la 7e à la 10e année, p. 14.
In order to develop a solid understanding, students need to have experiences in context by exploring problem situations. Contextualization allows students to make connections between various representations and to develop an understanding of the algebraic concepts being explored. Teachers also use a variety of representations to help students take ownership of mathematical concepts, make connections between representations, facilitate transfer, and elicit cognitive flexibility in relation to the concepts.
Mathematical argument is an essential tool for communication in mathematics. Students need to be able to justify their representations, ideas, and understanding using mathematical arguments, using a vocabulary of causal relationships (for example, if… therefore, because, since). Mathematical arguments allow students to present their understanding in a much more accurate and thoughtful way. For more information, see Communication and Learning: Conceptual and Practical Considerations for the Mathematics Classroom (Radford & Demers, 2004, pp. 15-25). A mathematical argument is an oral or written justification of a reasoning to demonstrate or refute a mathematical idea.
The mathematical exchange is the ideal moment to communicate mathematical representations and arguments. When solving a problem in algebra, students formulate conjectures, present their possible solutions, compare their ideas or justify their results using different representations. In short, students communicate.
Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 12-19.
Algebraic Reasoning: A Generalization of Arithmetic
As stated in Paying Attention to Algebraic Reasoning K-12, 'generalization is the heartbeat of mathematics.' (Mason, 1996, p. 65, as cited in Ontario Ministry of Education, 2013, p. 4)
When teachers want to develop students' algebraic reasoning from the generalization of arithmetic, it changes the learning goal.
Indeed, '… The focus of learning shifts from completing individual calculations to understanding the properties of and operations on numbers. This shift allows students to extend their understanding to other number systems (for example, fractions, decimals, integers) and to algebraic expressions.' (Ontario Ministry of Education, 2013, p. 6)
Helping students make generalizations allows them to deepen their learning beyond the original context and make connections between diverse knowledge.
This section will discuss the main objectives of the generalization of arithmetic, namely:
Operations and their properties
Much of the mathematics content related to numbering and number sense in grades 7 and 8 can be addressed with the goal of developing algebraic thinking. '… Rather than have students memorize properties or rules, allowing students to analyze many specific cases helps them move beyond thinking about multiple specific instances to thinking about the underlying mathematical generalization (Beatty & Bruce, 2012; Ontario Ministry of Education, 2005).'
The goal is to have students observe and analyze a situation and establish various relationships in order to formulate a generalization. Understanding the commutative, associative and distributive properties in numeration is a prerequisite for simplifying algebraic expressions and solving equations. Simplifying and solving equations also requires an understanding of the meaning of an equality situation and the meaning of the equal symbol.
Exploring the various properties of operations means examining the relationships between numbers, that is, analyzing situations in which the change of one quantity has an effect on another quantity.
Equality as a Relation Between Quantities
Algebra is about recognizing the relationships among quantities and operations. When students work with equations, it is imperative that they understand that the equal sign represents a relation between quantities rather than being a symbol to carry out a calculation. (Ontario Ministry of Education, 2013, p. 7)
In Paying Attention to Algebraic Reasoning K-12 (Ontario Ministry of Education, 2013), it is explained that '… many students do not recognize that the equal sign denotes equality' (p. 6), or even equivalence between two numerical expressions. '… most students see the equal sign as a signal to do something – to carry out a calculation and put the answer after the equal sign' (p. 6).
This idea comes from an association made with arithmetic where the learner is often asked to evaluate equations with the form: a [operation sign] b = ? Furthermore, the use of the calculator reinforces this idea, as the answer is displayed when the student presses the '=' key. Therefore, it is necessary to present students with arithmetic situations that require them to check whether equalities are true or false (for example, 14 + 3 = 16 + 1), as well as equalities with unusual forms (17 = 3 + 14). To facilitate the transition from arithmetic to algebraic reasoning, students need to develop some skills related to relationships between quantities.
The Transition to the Symbolic
Generalizations are expressed by symbols.
Traditionally, algebra has often been presented in high school as a predetermined syntax of rules and a symbolic language to be memorized by students. Students were expected to master symbolic manipulation before learning what the purpose and use of symbols were.
In other words, students were introduced to algebra with little opportunity to explore or make sense of it.
Exposing students to a variety of representations early in their learning helps them develop comfort with symbols. Continued exploration of the use of symbols in a variety of mathematical contexts allows students to make sense of and take ownership of these symbols. In particular, students gradually replace personal symbols with literal symbols to represent variables (for example, 13 + a = 19) and use them to communicate algebraic reasoning.
Source: translated from Guide d’enseignement efficace des mathématiques de la 7e à la 10e année, p. 32.
Teachers are vital in the development of algebraic thinking in the classroom. The teacher's role is not defined solely by the choice of tasks, but also by their interventions, which aim to encourage students to go beyond arithmetic reasoning and to access a symbolic way of thinking. Doing mathematics thus takes on its full meaning.
Some authors (for example, Blanton & Kaput, 2003, pp. 70-77) believe that teachers need 'algebraic eyes and ears' to identify and maximize connections to algebraic concepts in mathematical activities and to take advantage of opportunities to develop students' algebraic thinking.
To do this, the teacher can:
Vary the parameters of a problem
Use an existing problem and give it an algebraic perspective, promoting the search for relationships, patterns, conjectures and generalizations.
Example of a problem in the Numbers strand
In a team of four people, how many handshakes will there be if each person shakes hands with all the other people only once?
Starting from a number problem, the teacher asks questions that draw out connections to algebraic concepts, such as:
- How many handshakes will there be if one, two or three other people are added to the team?
- Organize the data in a table of values. Do you see a pattern?
- How many handshakes will there be if ten people are added to the team?
Ask questions to help students generalize
- What can be said about the relationship between the number of people on the team and the total number of handshakes?
- Is there a regularity? Explain your answer.
Ask questions with an emphasis on algebraic concepts
- Can you explain the problem in your own words?
- Can you solve the problem using another representation?
- How do we make sure that this solution is true?
- Would this approach work with other numbers? Always?
- What changes?
- What does not change?
These questions encourage students to make conjectures and explain them with mathematical arguments.
Develop and strengthen symbol literacy
Teachers need to introduce students to symbol literacy and support them in its development. Too often, the application of many of the mathematical symbols is done automatically, with students perceiving these symbols simply as a command to perform a mathematical operation. These students then have difficulty solving a problem correctly and explaining what the number sentence they have written represents because they do not understand the symbols that make up the sentence. The teacher's job is to put in place strategies that allow students to:
- read the symbols and think about what they represent before acting;
- understand the correct meaning of mathematical symbols (for example, the '=' sign represents a relationship between the numerical expressions on either side of the sign and is not a precursor to the answer);
- recognize and use symbols as communication tools to interpret a mathematical sentence and to express reasoning.
Creating an 'algebraic' learning environment: An 'algebraic' learning environment is one where the development of analytical thinking is emphasized. Teachers consciously identify times when reasoning is an integral part of their instruction. Arguing, abstracting, and generalizing become common practice during daily lessons in mathematics and even in other subjects, not an occasional enrichment.
Creating an 'algebraic' learning environment means giving students the chance to experience the world around them with 'algebraic' eyes and ears, that is, to be able to generalize explicitly.
Source: translated from Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, p. 23-24.