Fondements généraux du domaine Algèbre
Cycle intermédiaire
Introduction
« L’algèbre est le langage de communication privilégié des mathématiques. Les élèves doivent apprendre à utiliser l’algèbre comme outil de résolution de problèmes, c’est-à-dire comme un moyen de clarifier les concepts à un niveau abstrait avant de les appliquer. Le fait de connaître ce processus aide souvent les élèves à faire des généralisations et à approfondir leur apprentissage au-delà du contexte original. » (Ministère de l’Éducation de l’Ontario, 2005a, p. 10)

L’étude de l’algèbre s’est développée en partant du besoin de comprendre le monde réel et de le représenter. Au fil des siècles, les spécialistes des mathématiques ont tenté de résoudre des problèmes par l’observation de régularités et la représentation de phénomènes (par exemple, déterminer le diamètre de la Terre, prédire le mouvement des marées, expliquer le déplacement des objets en chute libre). Leurs travaux ont contribué au développement de symboles mathématiques et de méthodes de calcul.
Le ministère de l’Éducation de l’Ontario, dans le document Mettre l’accent sur le raisonnement algébrique M-12 (ministère de l’Éducation de l’Ontario, 2013), soutient que : « [le] raisonnement algébrique sous-tend toute la pensée mathématique, y compris l’arithmétique, car il nous permet d’explorer la structure des mathématiques. Nous reconnaissons maintenant l’importance d’inclure le raisonnement algébrique dans l’enseignement des mathématiques dès un très jeune âge, afin de rendre accessibles à tous les élèves ces idées mathématiques très efficaces.
Nous avons tous la capacité de penser algébriquement, car le raisonnement algébrique constitue, essentiellement, la façon dont les humains interagissent avec le monde. Dans notre quotidien, nous recherchons des régularités, nous prêtons attention à des aspects importants de ces régularités, puis nous faisons des généralisations tirées de situations familières pour les appliquer à des situations peu familières. » (p. 3)
C’est en abordant des situations concrètes que les élèves consolident leur compréhension des représentations d’une situation (mots, figures d’une suite à motif croissant, représentation graphique, table de valeurs et équation) et formalisent les idées mathématiques à l’aide de symboles algébriques (variables).
Le raisonnement algébrique
« Le raisonnement algébrique est présent dans tous les domaines mathématiques. Il consiste à décrire des régularités caractérisant des relations entre des quantités – contrairement à l’arithmétique qui consiste à effectuer des calculs portant sur des quantités connues. En gros, le raisonnement algébrique concerne la généralisation d’idées mathématiques et l’identification de structures mathématiques. » (Ministère de l’Éducation de l’Ontario, 2013, p. 3)
Dans un cours de mathématiques « […] visant à développer la pensée algébrique chez les élèves, l’objectif traditionnel de l’enseignement, apprendre à calculer, n’est pas omis; il est largement dépassé ». (Ministère de l’Éducation de l’Ontario, 2008a, p. 9)
Le raisonnement algébrique fait passer la compréhension qu’a l’élève des mathématiques au-delà des résultats de calculs et de l’application procédurale de formules. Toutefois, contrairement à l’apprentissage naturel des nombres, le développement d’un raisonnement algébrique requiert de penser autrement que de façon arithmétique de la part de l’apprenante ou de l’apprenant. L’acquisition de cette forme de raisonnement est progressive. Elle évolue avec l’expérience qu’acquiert l’élève en explorant des situations pouvant être généralisées.
Tout en tenant compte des éléments propres au développement du raisonnement algébrique, le personnel enseignant doit intégrer, dans son enseignement, les éléments essentiels d’un enseignement efficace des mathématiques, notamment les compétences liées à la communication et à la résolution de problèmes.
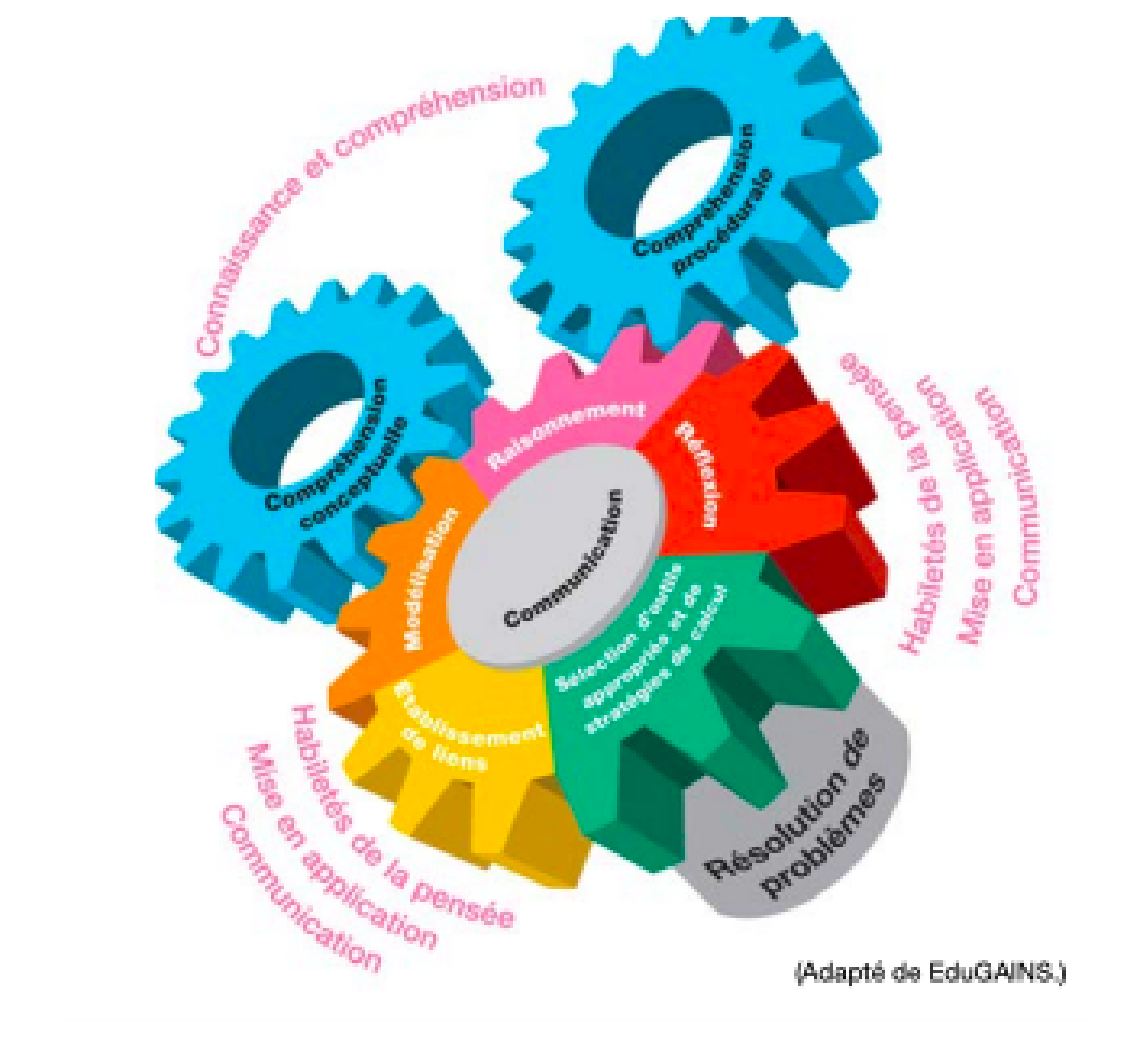 image Infographie. Un engrenage est placé sur un axe nommé « résolution de problèmes ». La roue d’engrenage, qui est sur cet axe, est divisée en 5 parties : la réflexion ; sélection d’outils appropriés et de stratégies de calcul ; établissement de liens ; modélisation ; et raisonnement. Le tout atournant autour de la communication. Ces cinq éléments permettent : les habiletés de la pensée, la mise en application et la communication. Sur les engrenages, modélisation et raisonnement, on retrouve une autre roue de compréhension conceptuelle, et une roue de compréhension procédure. Ce qui apportera la connaissance et compréhension.
image Infographie. Un engrenage est placé sur un axe nommé « résolution de problèmes ». La roue d’engrenage, qui est sur cet axe, est divisée en 5 parties : la réflexion ; sélection d’outils appropriés et de stratégies de calcul ; établissement de liens ; modélisation ; et raisonnement. Le tout atournant autour de la communication. Ces cinq éléments permettent : les habiletés de la pensée, la mise en application et la communication. Sur les engrenages, modélisation et raisonnement, on retrouve une autre roue de compréhension conceptuelle, et une roue de compréhension procédure. Ce qui apportera la connaissance et compréhension. Source : Guide d’enseignement efficace des mathématiques, de la 7e à la 10e année, p. 7-9.
Au cycle intermédiaire, le raisonnement algébrique évolue en faisant appel, dans des situations de plus en plus complexes, à l’abstraction et en mettant en pratique la généralisation et l’opération sur l’inconnue. Ces trois processus du raisonnement algébrique sont d’ordre « interactif » et non « hiérarchique ». Ils facilitent la résolution de problèmes et amènent l’élève à penser de façon algébrique.
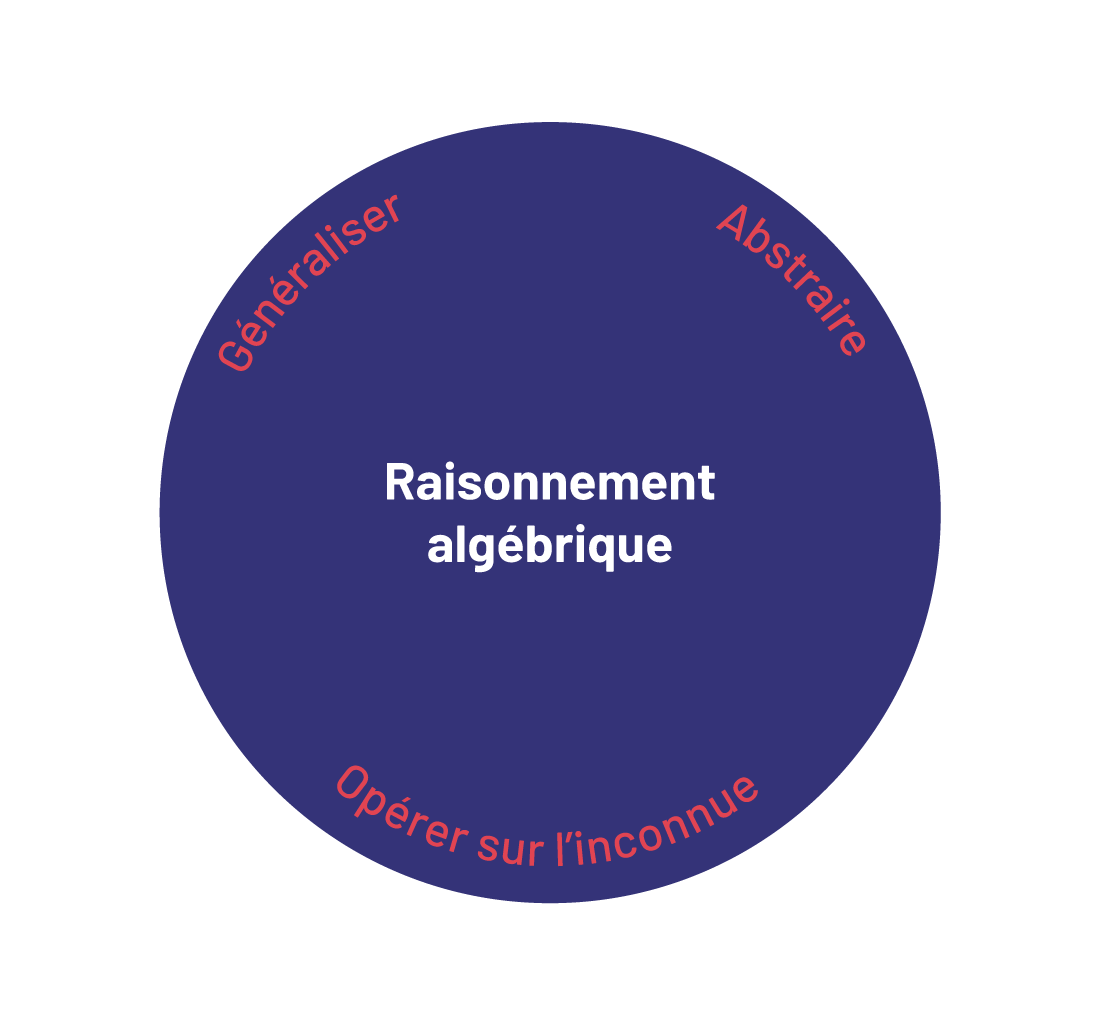
Abstraire
Abstraire est un des processus fondamentaux du raisonnement algébrique. « Abstraire, c’est se détacher de l’aspect sensoriel des choses pour raisonner à un niveau plus général (adapté de Raynal et Rieunier, 2003, p. 13), c’est se représenter mentalement une situation concrète, c’est passer à un niveau de conceptualisation plus profond. » (Ministère de l’Éducation de l’Ontario, 2008a, p. 9)
Exemple
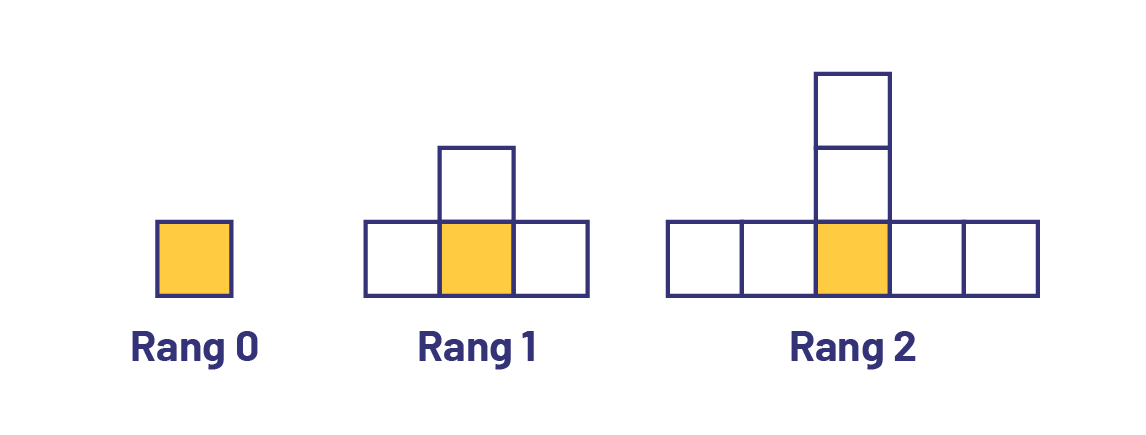 image Un exemple de raisonnement algébrique abstrait sur les carrés. Rang zéro : un carré jaune. Rang un : un carré jaune et un carré blanc sur le dessus, à droite et à gauche. Rang 2: un carré jaune, deux carrés blancs superposés verticalement et deux carrés blancs de chaque côté.
image Un exemple de raisonnement algébrique abstrait sur les carrés. Rang zéro : un carré jaune. Rang un : un carré jaune et un carré blanc sur le dessus, à droite et à gauche. Rang 2: un carré jaune, deux carrés blancs superposés verticalement et deux carrés blancs de chaque côté. | Niveau d'abstraction | Réflexion de l’élève |
|---|---|
| En analysant la suite croissante ci-dessus, il est fréquent que l’élève donne assez rapidement la description d’une figure quelconque. L’élève explique la suite sans la représenter concrètement : une première abstraction est alors développée. En se basant sur des figures particulières, l’élève dit pouvoir décrire la 10e figure et même la 100e figure. Toutefois, quel que soit le rang de la figure, l’explication demeure parfois longtemps ancrée dans le processus de construction de ces figures particulières. | Au rang 0, il y a un carré jaune. Au rang 1, il y a un carré jaune et un groupe de 3 carrés blancs. Au rang 2, il y a un carré jaune et deux groupes de 3 carrés blancs. Donc, au rang 3, il y aura un carré jaune et trois groupes de carrés blancs. La figure au rang 3 aura 3 groupes de 3 carrés blancs (3 × 3) + un carré jaune qui fait 10 en tout. Au rang 10, la figure aura 10 groupes de 3 carrés blancs (10 × 3) + 1 carré jaune, soit 31 carrés. |
| L’élève doit accomplir une seconde abstraction pour arriver à « […] une généralisation algébrique, c’est-à-dire [à] une généralisation dont la variable est exprimée par un nombre indéterminé » (Radford, Demers et Miranda, 2009, p. 16). L’élève exprime d’abord la règle en mots, puis effectue une généralisation à l’aide d’une équation. | Le nombre de carrés dans la figure est égal au numéro du rang × 3 et j’ajoute 1. Cela me donne le nombre de carrés qui composent la figure en question. Ou À l’aide d’une équation c = 3 × n + 1 (ou c = 3n + 1), où c représente le nombre de carrés et n, le numéro du rang, je décris n’importe quelle figure, quel que soit son rang. Note : Dans cette équation qui généralise la règle de la suite croissante, la règle est composée d’un multiplicateur (× 3) et d’une constante (+ 1). |
C’est le rôle du personnel enseignant de faire évoluer le niveau d’abstraction des élèves en leur offrant des occasions de faire de telles généralisations à l’aide de problèmes à difficulté croissante.
Généraliser
« Généraliser, c’est tirer des conclusions valables, vraies dans tous les cas, à partir de l’observation et de l’analyse de quelques exemples » (adapté de Squalli, 2002, p. 9, cité dans ministère de l’Éducation de l’Ontario, 2008a, p. 9).
Le raisonnement algébrique est fondé sur la capacité de remarquer l’existence de régularités, de similarités et de différences pour dégager des généralisations.
« La généralisation est au cœur des mathématiques et se manifeste sous de nombreuses formes. Si les enseignantes et enseignants […] n’ont pas l’habitude de demander aux élèves d’exprimer leurs propres généralisations, la pensée mathématique n’est pas présente. » (Mason, 1996, p. 65, cité dans ministère de l’Éducation de l’Ontario, 2013, p. 4)
Pour amener les élèves à généraliser, le personnel enseignant doit modeler une marche à suivre favorisant le raisonnement algébrique. Cette marche à suivre engage l’élève à réaliser trois étapes : la proposition d’une conjecture, la vérification de cette conjecture et la formulation d’une généralisation.
« Une conjecture est l’expression d’une idée perçue comme étant vraie dans toute situation semblable. » (Ministère de l’Éducation de l’Ontario, 2008a, p. 10)
Le mot conjecture s’apparente au mot hypothèse utilisé davantage dans les attentes et les contenus d’apprentissage du programme-cadre; par exemple, « formuler une hypothèse quant à l’existence d’une relation entre deux variables. » (Ministère de l’Éducation de l’Ontario, 2005b, p. 30)
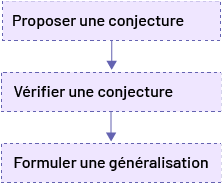
Aider les élèves à généraliser, c’est :
- les guider dans l’observation et l’analyse de situations;
- les initier à proposer des conjectures;
- leur demander d’appuyer leurs conjectures à l’aide de représentations mathématiques ou d’arguments mathématiques;
- les inviter à vérifier leurs conjectures dans d’autres situations;
- les accompagner dans la formulation d’une généralisation, si cela est possible.
Exemple
Abdel remet aux élèves un rectangle et leur demande d’en déterminer l’aire. Puis, il les invite à proposer une conjecture relative à la mesure de l’aire. « Si la mesure de la base du rectangle est doublée, qu’arrive-t-il à la mesure de l’aire? »
Un élève propose une conjecture : « L’aire va aussi doubler. »
Pour vérifier la conjecture, l’enseignant demande aux élèves de doubler la longueur de la base et de déterminer l’aire du nouveau rectangle.
Ensuite, il les invite à analyser les résultats afin de déterminer ce qui arrive à l’aire d’un rectangle lorsque la mesure de sa base est doublée.
Puis, il demande aux élèves de vérifier si la conjecture est vraie pour d’autres rectangles.
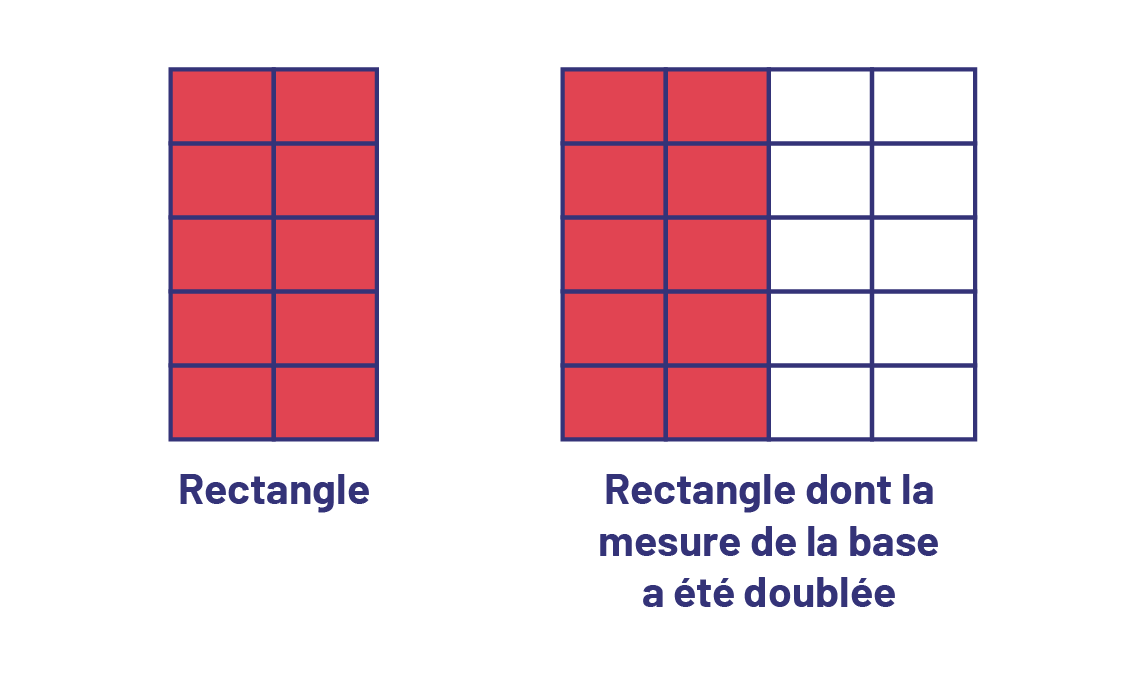 image Exemple d'une suite de carrés rouges dont la base est doublée. Rectangle un: 5 carrés rouges superposés verticalement répétés 2 fois. Rectangle 2: 5 carrés rouges superposés verticalement répétés 2 fois. Rectangle 3 : 5 carrés blancs superposés verticalement répétés 2 fois.
image Exemple d'une suite de carrés rouges dont la base est doublée. Rectangle un: 5 carrés rouges superposés verticalement répétés 2 fois. Rectangle 2: 5 carrés rouges superposés verticalement répétés 2 fois. Rectangle 3 : 5 carrés blancs superposés verticalement répétés 2 fois. Reconnaissant que leur conjecture semble s’appliquer à toutes les situations similaires, les élèves peuvent formuler une généralisation en ayant recours à des mots ou en se servant de symboles.
Raisonnement de l’élève : Si la longueur de la base d’un rectangle est doublée, l’aire du rectangle est aussi doublée.
Si b × h = A, alors 2b × h = 2A.
Lorsque le développement du raisonnement algébrique devient un objectif d’apprentissage, le personnel enseignant propose aux élèves différentes explorations pour qu’elles et ils soient en mesure de généraliser. Ces différentes explorations devraient amener les élèves à faire des généralisations sur les propriétés des nombres en partant de l’observation de suites à motif croissant, et à découvrir des formules et des généralisations relatives à la mesure et à la géométrie.
Opérer sur l’inconnue
Opérer sur l’inconnue, c’est l’action d’analyser et d’agir sur ce qui est inconnu. « C’est raisonner de manière analytique, c’est réfléchir sur les opérations, les généralisations et non sur les objets (adapté de Squalli et Theis, 2005). » (Ministère de l’Éducation de l’Ontario, 2008a, p. 11)
Note : On fait allusion ici à l’inconnu dans le sens large du mot et non à l’inconnue dans le sens d’un symbole ou d’une valeur que l’on ne connaît pas.
C’est aussi examiner les éléments d’une opération, d’une suite numérique pour en dégager le changement. En d’autres mots, « [l]e raisonnement algébrique […] permet de manipuler n’importe quelle quantité inconnue comme si elle était connue ». (Ministère de l’Éducation de l’Ontario, 2013, p. 4)
L’inconnue, les variables et les symboles permettent d’observer et de décrire les actions posées pour résoudre un problème et en dégager une généralisation.

Source : Guide d’enseignement efficace des mathématiques, de la 7e à la 10e année, p. 10-13.
« Raisonner à l’aide de concepts et de processus mathématiques ne peut logiquement se faire que si l’on communique avec le langage mathématique et le raisonnement mathématique s’exerce le plus généralement en situation de résolution de problèmes. » (Ministère de l’Éducation du Québec, 2001, p. 125)
La pensée algébrique des élèves se développe en relation avec le développement d’habiletés mathématiques. Ainsi, les élèves doivent développer leur habileté à raisonner et à résoudre des problèmes de façon algébrique, puis à communiquer leur raisonnement algébrique.
Habileté à raisonner de façon algébrique
L’habileté à raisonner de façon algébrique permet aux élèves d’examiner des situations et d’organiser leur pensée. Alors que l’arithmétique est généralement perçue comme un calcul sur des quantités connues, misant à trouver la bonne réponse, le raisonnement algébrique vise à mieux comprendre la numération en permettant d’analyser les relations entre les nombres pour trouver une valeur. C’est pourquoi il est primordial de développer, à l’élémentaire, l’habileté à raisonner de façon algébrique, plus particulièrement dans des situations de résolution de problèmes.
Selon Driscoll (1999, p. 1-19), le raisonnement algébrique inclut l’habileté à « faire et défaire », l’habileté à créer des règles pour représenter des relations entre deux quantités en changement et l’habileté à formuler des généralisations au sujet des propriétés des opérations arithmétiques.
L’habileté à « faire et défaire » se manifeste lorsque les élèves réussissent à procéder à rebours. Par exemple, les élèves peuvent faire appel aux liens entre l’addition et la soustraction et entre la multiplication et la division. Étant donné l’équation Δ + 3 = 11, l’élève qui peut procéder à rebours comprend que l’on peut soustraire 3 de la somme (11 – 3 = 8) pour déterminer la valeur inconnue, car on a ajouté 3 à la variable pour obtenir une somme de 11. Il s’agit d’un raisonnement algébrique, puisque l’action est effectuée en fonction d’une réflexion et d’une compréhension, et non d’une procédure pour laquelle l’élève ne peut en expliquer le sens.
L’habileté à créer des règles pour représenter des relations fait appel à l’habileté à généraliser à partir de règles. Par exemple, dans la suite croissante ci-dessous, l’élève qui raisonne algébriquement peut d’abord reconnaître qu’au rang 1, la figure est composée de 1 colonne de 2 points, qu’au rang 2, la figure est composée de 2 colonnes de 3 points… Ainsi, l’élève peut généraliser et représenter la relation entre le nombre de points (p) et le numéro du rang (n) par une équation [par exemple, p = n × (n + 1)].
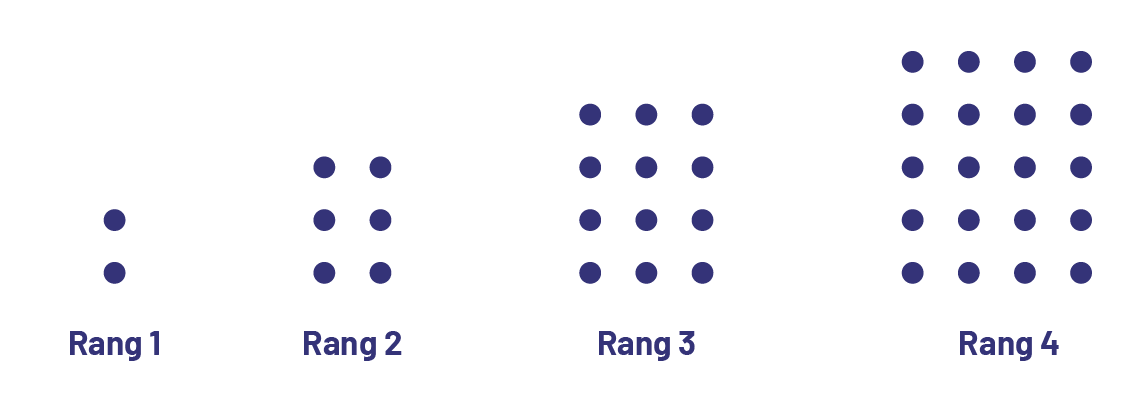
L’habileté à généraliser les propriétés des opérations arithmétiques démontre aussi un raisonnement algébrique (par exemple, savoir que l’on peut changer l’ordre de deux nombres que l’on veut additionner sans affecter la somme ou que le produit d’un nombre et de 1 est toujours égal au nombre).
Le raisonnement algébrique se distingue aussi du raisonnement arithmétique de la façon suivante. Le raisonnement arithmétique porte plutôt sur des situations statiques, alors que le raisonnement algébrique porte davantage sur des situations en changement. En développant le raisonnement algébrique des élèves, on leur permet de voir et d’analyser des situations plus englobantes et de développer leur répertoire de stratégies de résolution de problèmes.
Pour stimuler le raisonnement algébrique des élèves, le personnel enseignant peut utiliser un problème arithmétique existant et lui donner une perspective algébrique en ajoutant une situation en changement. Ces situations favorisent la recherche de régularités et de relations, l’utilisation de variables ainsi que l’expression de justifications, de conjectures et de généralisations.
Le tableau ci-dessous fait ressortir la différence entre un problème qui suscite un raisonnement arithmétique et un problème qui suscite un raisonnement algébrique.
| Raisonnement arithmétique | Raisonnement algébrique |
|---|---|
On travaille à partir d’une situation statique. Exemple Ce problème présente une situation statique. Il admet une seule réponse qu’il faut déterminer à l’aide d’opérations arithmétiques. | On travaille à partir d’une situation en changement. Exemple
Ce problème présente une situation en changement. Il porte sur l’étude de règle de régularité et surtout de règle de correspondance (relation entre deux quantités en changement). |
En raisonnant algébriquement, les élèves analysent les nombres, les symboles, les quantités et les opérations, puis généralisent.
Voici un autre exemple où on peut observer la différence entre un raisonnement algébrique et un raisonnement arithmétique.
Dans l’image ci-dessous, il y a le même nombre de carrés de chaque côté de la flèche. Combien de carrés y a-t-il sous la cloche?
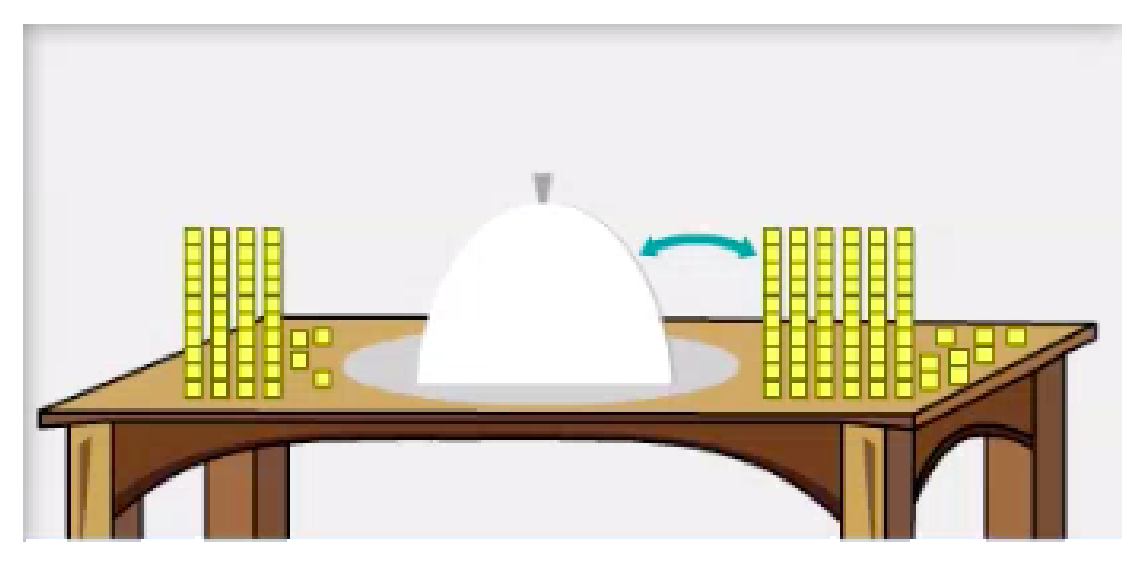 image Exemple de raisonnement algébrique et arithmétique d'un tableau comportant des carrés des deux côtés. Le côté droit a 6 colonnes de 10 carrés jaunes et 8 carrés jaunes sur le côté. Le côté gauche a 4 colonnes de 10 carrés jaunes et 4 carrés jaunes sur le côté. Une flèche bleue part des carrés jaunes et se dirige vers la cloche située au milieu du tableau.
image Exemple de raisonnement algébrique et arithmétique d'un tableau comportant des carrés des deux côtés. Le côté droit a 6 colonnes de 10 carrés jaunes et 8 carrés jaunes sur le côté. Le côté gauche a 4 colonnes de 10 carrés jaunes et 4 carrés jaunes sur le côté. Une flèche bleue part des carrés jaunes et se dirige vers la cloche située au milieu du tableau.Cliquer sur l’image pour constater la différence entre les deux raisonnements.
Source : L’@telier - Ressources pédagogiques en ligne (atelier.on.ca).
La capacité de raisonner algébriquement ne se développe pas de façon simple et naturelle. C’est pourquoi le personnel enseignant doit faire cheminer les élèves en les incitant :
- à expliciter leur raisonnement;
- à travailler à rebours;
- à analyser les liens entre les quantités et à organiser l’information pour représenter une situation d’une autre façon;
- à proposer des conjectures et à généraliser.
Dans le cadre de situations d’apprentissage, le personnel enseignant doit poser des questions qui mettent l’accent sur des concepts algébriques et qui amènent les élèves à réfléchir.
En voici quelques exemples :
- Est-ce que ça fonctionne si je fais la même chose avec d’autres nombres?
- Qu’est-ce qui change? Qu’est-ce qui ne change pas?
- Est-ce que l’information recueillie me permet de prédire le résultat?
- Est-ce que la règle peut être appliquée à n’importe quel cas?
- Est-ce que je suis toujours les mêmes étapes? Quelles sont-elles?
Habileté à résoudre une situation-problème de façon algébrique
La résolution d’une situation-problème vise à engager les élèves dans un processus où seront utilisées différentes stratégies. Les élèves qui ont développé des stratégies ont plus de facilité à amorcer la résolution d’une situation-problème, à anticiper et à prédire des résultats, à raisonner et à trouver une solution.
Une situation-problème désigne un problème qui :
- est en contexte;
- permet d’utiliser différentes stratégies;
- représente un défi pour l’élève.
Voici une situation-problème qui peut être résolue de façon arithmétique ou algébrique.
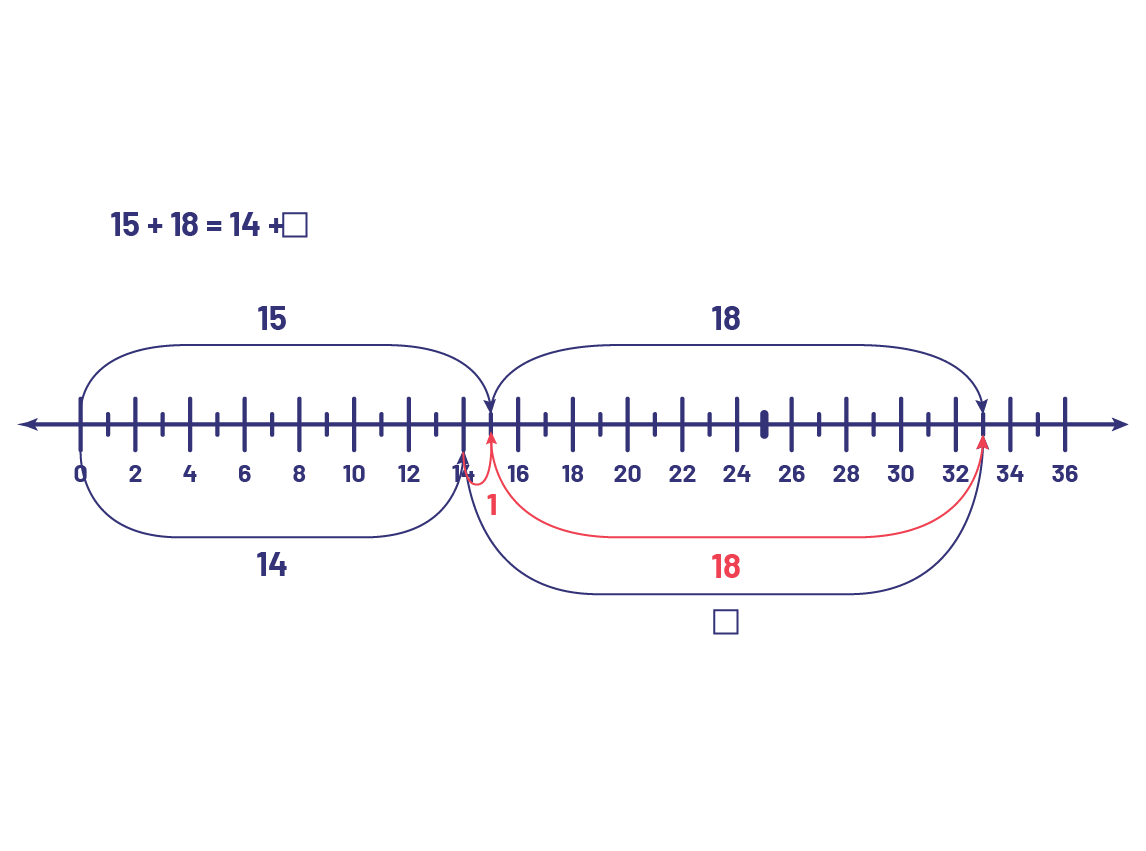
Sylvia a 15 poissons rouges et 18 poissons à rayures jaunes. Jacob a le même nombre de poissons, mais seulement 14 de ses poissons sont rouges. Combien Jacob a-t-il de poissons à rayures jaunes?

| Résolution à l’aide d’un raisonnement arithmétique | Résolution à l’aide d’un raisonnement algébrique |
|---|---|
| Je sais que Sylvia a 33 poissons en tout, car 15 plus 18, c’est 33. 15 + 18 = 33 Jacob a le même nombre de poissons. Alors s’il a 14 poissons rouges, il en a 19 qui ont des rayures jaunes, car 33 moins 14, c’est 19. 33 – 14 = 19 On effectue des opérations arithmétiques pour résoudre le problème. | Je sais que Sylvia et Jacob ont le même nombre de poissons. 15 + 18 = 14 + □ Si Sylvia a 15 poissons rouges et Jacob en a 14, alors Jacob a 1 poisson rouge de moins que Sylvia. 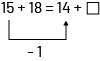 Puisque Jacob a le même nombre de poissons que Sylvia, il doit avoir 1 poisson à rayures jaunes de plus que Sylvia. 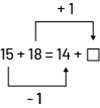 image Équation arithmétique : 15, plus, 18, égal, 14, plus, carré. Une flèche pointant de la valeur 15 à la valeur 14, montrant une équation en équilibre avec la valeur moins un. Une flèche pointant de la valeur 18 vers le symbole du carré, montrant une équation en équilibre avec une valeur de plus un. image Équation arithmétique : 15, plus, 18, égal, 14, plus, carré. Une flèche pointant de la valeur 15 à la valeur 14, montrant une équation en équilibre avec la valeur moins un. Une flèche pointant de la valeur 18 vers le symbole du carré, montrant une équation en équilibre avec une valeur de plus un.Donc □ = 19. Au lieu d’effectuer des calculs, on interprète le problème et on compare les quantités. On peut représenter la situation par une équation. Pour la résoudre, on compare les quantités de chaque côté du signe « = ». |
En général, les élèves ont tendance à résoudre un tel problème de façon arithmétique. Le personnel enseignant peut alors varier les paramètres du problème en lui donnant une perspective algébrique, par exemple, en demandant aux élèves de représenter la situation-problème à l’aide d’une équation. Pour résoudre l’équation, les élèves peuvent utiliser une droite numérique, ce qui peut les aider à réfléchir au calcul et non à faire le calcul. L’important n’est pas d’effectuer un calcul, mais de bien saisir la relation d’égalité entre les deux expressions numériques.
Habileté à communiquer un raisonnement algébrique
« La communication bénéficie à tous ceux qui participent à l’échange […]. L’obligation de faire part de sa compréhension d’une situation ou d’un concept contribue souvent à l’amélioration ou à l’approfondissement de cette compréhension. » (Ministère de l’Éducation du Québec, 2001, p. 132)
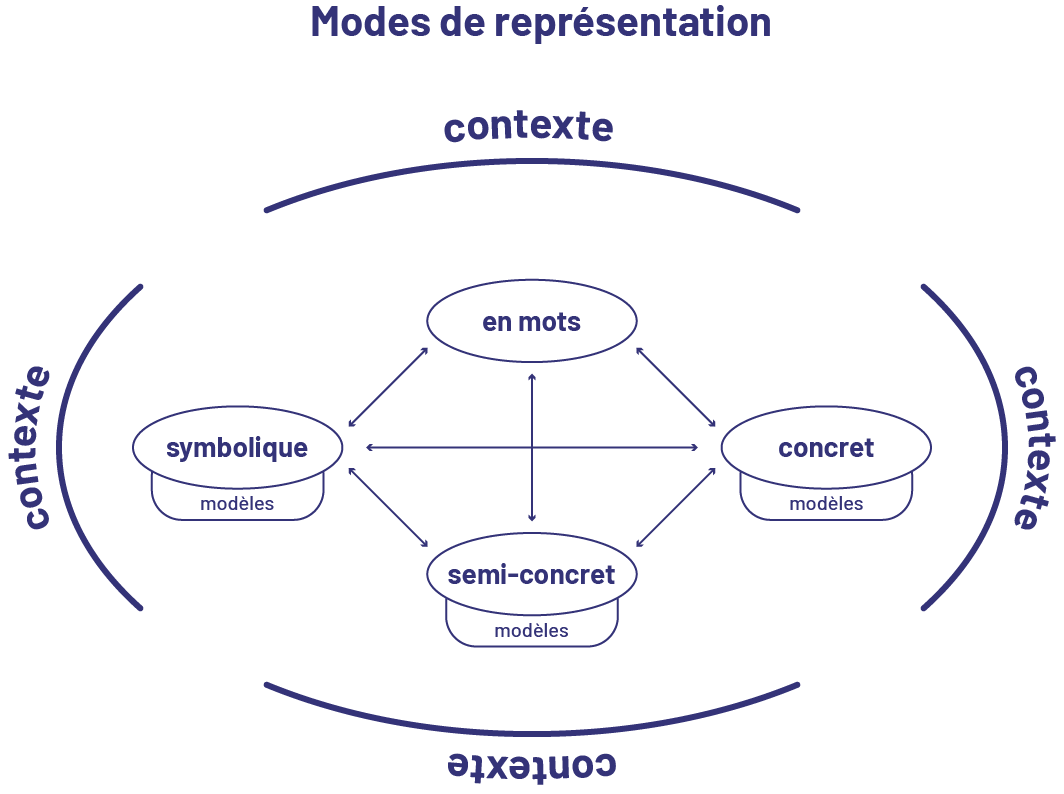
L’habileté à communiquer un raisonnement algébrique se développe lorsque les élèves expriment leur compréhension d’une situation-problème ou d’un concept, et défendent leurs idées en utilisant différents modes de représentation :
- le mode concret, lié à l’exploration, à la manipulation et à la création à l’aide de matériel concret;
- le mode semi-concret, lié à une illustration, à un dessin ou à toute autre représentation sur papier;
- le mode symbolique, lié à toute représentation faite à partir de chiffres ou de symboles;
- le mode « en mots », lié à une explication ou à une description verbale ou écrite.
Source : Algèbre, Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 12-18.
Les élèves montrent leur compréhension des relations à l’aide de différentes représentations : relation en situation (mots, figures d’une suite croissante), table de valeurs, équation et représentation graphique.
Il est important pour les élèves de la 7e et de la 8e année de continuer à représenter une situation à l’aide de matériel concret, de matériel semi-concret et de mots avant de passer à la représentation symbolique. L’analyse de suites croissantes les aide à développer leur habileté à traduire une situation en équation. Les élèves parviennent à la généralisation algébrique en remplissant une table de valeurs, en décrivant verbalement des figures occupant des rangs plus loin dans la suite et en analysant des expressions numériques. Il importe aussi que les élèves associent des suites croissantes à une histoire en contexte.

Source : Guide d’enseignement efficace des mathématiques, de la 7e à la 10e année, p. 14.
Afin d’acquérir une solide compréhension, les élèves doivent vivre des expériences en contexte en explorant des situations-problèmes. La mise en contexte permet aux élèves d’établir des liens entre diverses représentations et de développer une compréhension des concepts algébriques explorés. Le personnel enseignant utilise aussi diverses représentations afin d’aider les élèves à s’approprier les concepts mathématiques et à établir des liens entre les représentations.
L’argument mathématique est un outil essentiel de communication en mathématiques. Les élèves doivent parvenir à justifier leurs représentations, leurs idées et leur compréhension à l’aide d’arguments mathématiques, en se servant d’un vocabulaire de relations causales (par exemple, si… donc, parce que, puisque). Les arguments mathématiques permettent aux élèves de présenter leur compréhension de façon beaucoup plus juste et réfléchie. Pour plus de renseignements à ce sujet, consulter le document intitulé Communication et apprentissage : Repères conceptuels et pratiques pour la salle de classe de mathématiques (Radford et Demers, 2004, p. 15-25). Un argument mathématique est une justification orale ou écrite d’un raisonnement dans le but de démontrer ou de réfuter une idée mathématique.
L’échange mathématique est le moment idéal pour communiquer des représentations et des arguments mathématiques. Au moment de résoudre une situation-problème en algèbre, les élèves formulent des conjectures, présentent leurs pistes de solution, confrontent leurs idées ou justifient leurs résultats à l’aide de différentes représentations. Bref, les élèves communiquent.
Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 18-19.
Le raisonnement algébrique : une généralisation de l'arithmétique
« La distinction entre un raisonnement arithmétique et un raisonnement algébrique réside précisément dans le caractère analytique du raisonnement et non sur l’absence ou la présence de lettres pour représenter les inconnues. » (Adihou et collab., 2016, p. 209)
Comme le précise le document Mettre l’accent sur le raisonnement algébrique M-12, « la généralisation est au cœur des mathématiques […] ». (Mason, 1996, p. 65, cité dans ministère de l’Éducation de l’Ontario, 2013, p. 4)
Lorsque le personnel enseignant désire développer chez les élèves le raisonnement algébrique en partant de la généralisation de l’arithmétique, cela modifie l’objectif d’apprentissage.
En effet, celui-ci : « […] devient la compréhension des propriétés des nombres et des opérations sur ceux-ci, plutôt que le fait d’effectuer des calculs. Ce changement permet aux élèves d’appliquer leurs connaissances à d’autres systèmes de nombres (par exemple, fractions, décimales, nombres entiers) et à des situations algébriques. » (Ministère de l’Éducation de l’Ontario, 2013, p. 6)
Aider les élèves à faire des généralisations leur permet d’approfondir leur apprentissage au-delà du contexte original et d’établir des liens entre diverses connaissances.
Cette section traitera des principaux objectifs de la généralisation de l’arithmétique soit :
Les opérations et leurs propriétés
La plupart des contenus mathématiques liés au domaine Nombres, de la 7e et de la 8e année, peuvent être abordés en misant sur l’objectif de développer la pensée algébrique. Au lieu de demander aux élèves de mémoriser des règles pour effectuer des opérations sur différents nombres, il est plus efficace de « […] les amener à dépasser ces cas particuliers et arriver à penser à la généralisation mathématique sous-jacente (Beatty et Bruce, 2012; ministère de l’Éducation de l’Ontario, 2005) ». (Ministère de l’Éducation de l’Ontario, 2013, p. 6)
L’objectif est d’amener les élèves à observer et à analyser une situation, ainsi qu’à établir diverses relations en vue de formuler une généralisation. La compréhension des propriétés telles que la commutativité, l’associativité et la distributivité en numération est un préalable à la simplification d’expressions algébriques et à la résolution d’équations. Simplifier et résoudre des équations exigent aussi une bonne compréhension du sens d’une situation d’égalité et du sens du symbole égal.
Explorer les diverses propriétés des opérations, c’est examiner les relations entre les nombres, c’est-à-dire analyser des situations dans lesquelles le changement d’une quantité a un effet sur une autre quantité.
Source : Guide d’enseignement efficace des mathématiques, de la 7e à la 10e année, p. 17-18
L’égalité en tant que relation entre des quantités
« L’algèbre consiste à reconnaître les relations entre des quantités et des opérations. Lorsque des élèves travaillent avec des équations, il est impératif qu’ils comprennent que le signe égal représente une relation entre des quantités plutôt qu’un symbole indiquant qu’il faut effectuer un calcul. » (Ministère de l’Éducation de l’Ontario, 2013, p. 7)
Dans Mettre l’accent sur le raisonnement algébrique M-12 (ministère de l’Éducation de l’Ontario, 2013), il est expliqué que « […] de nombreux élèves ne reconnaissent pas que le signe égal indique une égalité » (p. 6), voire une équivalence entre deux expressions numériques. La « […] plupart des élèves ont interprété le symbole égal comme étant synonyme d’effectuer un calcul et [d’] inscrire la réponse après le symbole égal » (p. 6).
Cette idée relève d’une association faite avec l’arithmétique où souvent il est demandé à l’apprenante ou à l’apprenant d’évaluer des équations ayant la forme : a [signe d’opération] b = ?. De plus, l’utilisation de la calculatrice renforce cette idée, puisque la réponse est affichée lorsque l’élève appuie sur la touche « = ». Il est donc nécessaire de présenter aux élèves des situations arithmétiques qui leur demandent de vérifier si des égalités sont vraies ou fausses (par exemple, 14 + 3 = 16 + 1), ainsi que des égalités ayant des formes inhabituelles (17 = 3 + 14). Pour faciliter le passage du raisonnement arithmétique au raisonnement algébrique, les élèves doivent développer certaines habiletés relatives aux relations entre des quantités.
Source : Guide d’enseignement efficace des mathématiques, de la 7e à la 10e année, p. 26
Le passage au symbolique
Les généralisations sont exprimées par des symboles.
Traditionnellement, l’algèbre a souvent été présentée au secondaire comme une syntaxe prédéterminée de règles et un langage symbolique devant être mémorisé par les élèves. On s’attendait à ce que les élèves maîtrisent la manipulation symbolique avant d’apprendre ce qu’étaient le but et l’utilisation des symboles.
Autrement dit, on a présenté l’algèbre aux élèves en leur donnant peu de possibilités de l’explorer ou d’y trouver un sens.
Exposer les élèves à une variété de représentations tôt dans leur apprentissage les aide à développer une aisance avec les symboles. L’exploration continue de l’utilisation de symboles dans des contextes mathématiques variés permet aux élèves de donner un sens à ces symboles et à se les approprier. Notamment, les élèves remplacent progressivement les symboles personnels par des symboles littéraux pour représenter des variables (par exemple, 13 + a = 19) et les utilisent pour communiquer un raisonnement algébrique.
Source : Guide d’enseignement efficace des mathématiques, de la 7e à la 10e année, p. 32.
Le personnel enseignant demeure le pivot de l’actualisation du développement de la pensée algébrique. Son rôle ne se définit pas uniquement dans le choix des tâches, mais bien dans ses interventions qui visent à encourager les élèves à dépasser le raisonnement arithmétique et à accéder à un mode de pensée symbolique. Faire des mathématiques prend ainsi tout son sens.
Certains auteurs et auteures (par exemple, Blanton et Kaput, 2003, p. 70-77) croient que le personnel enseignant doit se munir « d’yeux et d’oreilles algébriques » afin de déterminer et de maximiser, dans les activités mathématiques, les liens avec les concepts algébriques et de saisir des occasions pour développer la pensée algébrique des élèves.
Pour ce faire, il peut :
Varier les paramètres d’un problème
Utiliser un problème existant et lui donner une perspective algébrique favorise la recherche de relations, de régularités, de conjectures et de généralisations.
Exemple de problème du domaine Nombres :
Dans une équipe de quatre personnes, combien de poignées de main y aura-t-il si chaque personne donne la main à toutes les autres personnes une seule fois?
À partir d’un problème de numération, le personnel enseignant pose des questions qui permettent de faire ressortir les liens avec les concepts algébriques, telles que :
- Combien y aura-t-il de poignées de main si une, deux ou trois autres personnes s’ajoutent à l’équipe?
- Organiser les données dans une table de valeurs. Est-ce que vous voyez une régularité?
- Combien de poignées de main y aura-t-il si dix personnes s’ajoutent à l’équipe?
Poser des questions pour aider les élèves à généraliser
- Que peut-on dire au sujet de la relation entre le nombre de personnes dans l’équipe et le nombre total de poignées de main?
- Y a-t-il une régularité? Expliquez votre réponse.
Poser des questions en mettant l’accent sur les concepts algébriques
- Pouvez-vous expliquer le problème dans vos mots?
- Pouvez-vous résoudre le problème à l’aide d’une autre représentation?
- Comment fait-on pour s’assurer que cette solution est vraie?
- Est-ce que cette démarche fonctionnerait avec d’autres nombres? Toujours?
- Qu’est-ce qui change?
- Qu’est-ce qui ne change pas?
Ces questions incitent les élèves à faire des conjectures et à les expliquer à l’aide d’arguments mathématiques.
Développer et renforcer une littératie des symboles
Le personnel enseignant doit initier les élèves à la littératie des symboles et les soutenir dans le développement de celle-ci. Trop souvent, l’application de plusieurs des symboles mathématiques se fait par automatisme, ces symboles étant perçus par des élèves simplement comme une commande d’exécution d’une opération mathématique. Ces élèves éprouvent alors des difficultés à résoudre un problème correctement et à expliquer ce que représente la phrase mathématique qu’elles et ils ont écrite, faute de compréhension des symboles qui la composent. Le travail du personnel enseignant consiste à mettre en place les stratégies qui permettent aux élèves :
- de lire les symboles et de réfléchir à ce qu’ils représentent avant d’agir;
- de comprendre la juste signification des symboles mathématiques (par exemple, le signe « = » représente une relation entre les expressions numériques de chaque côté du signe et n’est pas précurseur de la réponse);
- de reconnaître et d’utiliser les symboles comme outils de communication pour interpréter une phrase mathématique et pour exprimer son raisonnement.
Créer un milieu d’apprentissage « algébrique » : Un milieu d’apprentissage « algébrique » est un environnement où l’on mise sur le développement de la pensée analytique. Le personnel enseignant, de façon consciente, détermine et cerne des moments où le raisonnement fait partie intégrante de son enseignement. Argumenter, abstraire et généraliser devient pratique courante pendant des leçons quotidiennes en mathématiques et même dans les autres matières, et non un enrichissement occasionnel.
Créer un milieu d’apprentissage « algébrique », c’est donner la chance aux élèves de découvrir le monde qui les entoure avec des yeux et des oreilles « algébriques », c’est-à-dire d’être capables de généraliser de façon explicite.
Source : Guide d’enseignement efficace des mathématiques, de la maternelle à la 3e année, p. 23-24.

