General Foundations of Algebra
Junior Division
Introduction
The Algebra strand brings together concepts essential to mathematics and used for representing and analyzing relationships found in many everyday situations.
The study of algebra developed from the need to understand and represent the real world, for example, the position of planets, the movement of tides, the movement of falling objects. Mathematicians tried to solve these questions by observing regularities and modelling the phenomena with equations and graphical representations. This work has contributed to the development of mathematical symbols and methods of calculation. Now, 'in this new millennium, algebra is no longer a discipline that dwells on the manipulation of symbols. Algebra becomes a way of thinking, a way of seeing and expressing relationships.' (Ontario Ministry of Education, 2000, p. 26)
In the junior grades, students observe changes in the world around them and describe and represent them first in concrete and visual (semi-concrete) ways and then in symbolic ways.
For example, the growing pattern below is used to represent a situation. Students learn to describe the regularities that can be seen from one term to the next, to express the relationship between the position and the number of cubes in the term, and to represent this relationship by a table of values and by an equation.

Students should observe that there is one constant (+1), the blue cube that does not change from one term to the next.
Students should also observe the relationship between the term number and the term value to determine the pattern rule: number of cubes = term number × 2 + 1. In this case, it is a pattern rule with a multiplier (the part that makes the pattern grow) and a constant. This rule allows them to make far predictions.
Algebraic Thinking
In the Primary and Junior Divisions, the main goal of the Algebra strand is to develop students' algebraic thinking. In the search for a definition of algebraic thinking, several authors emphasize a perspective that is considered essential in algebra.
Of the many elements that contribute to effective teaching and modelling of algebra, some have a greater impact on the development of algebraic thinking, namely a focus on:
- fundamental processes to access higher levels of abstraction (abstracting, generalizing and operating on variables);
- mathematical skills developed from an algebraic perspective (problem solving, reasoning and communication);
- components of the learning environment (understanding relationships, representing with symbols, using models, and analyzing change);
- algebraic concepts grouped according to a big idea (relationships).
The image below illustrates the interaction between these factors.
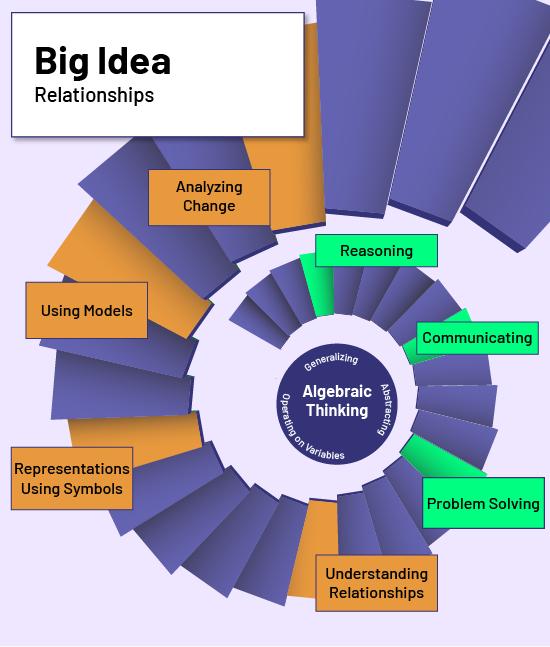 image Infographics: Big ideas. Patterns and relationships. Expressions and equality. A descending spiral staircase with the following words spiraling down with the staircase. Analyze change, Use models, Represent with symbols, Understand relationships, Solve a problem, Communicate, Reason. At the bottom of the spiral staircase is a circle with the following words inside: Algebraic Thinking, Generalize, Abstract, Operate on a variable.
image Infographics: Big ideas. Patterns and relationships. Expressions and equality. A descending spiral staircase with the following words spiraling down with the staircase. Analyze change, Use models, Represent with symbols, Understand relationships, Solve a problem, Communicate, Reason. At the bottom of the spiral staircase is a circle with the following words inside: Algebraic Thinking, Generalize, Abstract, Operate on a variable.
Algebraic Concepts Grouped According to A Big Idea
The overall and specific expectations in Algebra involve a large number of concepts. Grouping these concepts under big ideas helps to plan more effective instructional programming. In doing so, teachers are able to develop coherent learning situations that allow students to:
- explore concepts in depth;
- make connections between the different concepts;
- develop algebraic thinking.
A big idea is a statement of an idea that is fundamental to learning mathematics, an idea that ties together a lot of mathematical knowledge into a coherent whole.
The big idea of "Relationships" forms the basis of the expectations for the Algebra strand in grades 4 to 6. This big idea places the understanding of relationships between quantities or numbers at the centre of all algebra learning. Its development in terms of the two underlying concepts, exploring relationships and the meaning of symbols, helps teachers identify and prioritize important learning and implement effective and consistent instructional strategies.
Understanding the relationships between quantities or numbers in mathematical situations with or without context is the basis of algebraic thinking.
| BIG IDEA 1: Relationships |
|---|
|
Key Point 1 - Exploring Relationships Analyzing situations involving changing quantities helps us to establish the mathematical relationship between them. |
|
Key Point 2 - Meaning of Symbols Symbols have meanings that help us to interpret and represent relationships between quantities or numbers in mathematical situations. |
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 30.
Developing algebraic thinking is a complex journey that relies on three fundamental processes: abstracting, generalizing, and operating on unknown quantities.
Abstracting
To abstract is 'to dismiss by thought, to disregard' (Le nouveau Petit Robert, 2006, p. 11). Abstraction is one of the characteristics of algebraic thinking. In the primary grades, students learn that no matter what objects are involved, two objects plus two objects is four objects. To understand this concept, students do not consider the objects per se, but focus on their number. To abstract is to detach oneself from the sensory aspect of things in order to reason at a more general level (adapted from Raynal & Rieunier, 2003, p. 13), to mentally represent a concrete situation, to move to a deeper level of conceptualization. Piaget considers abstraction to be one of the basic processes in the construction of knowledge. For his part, Roegiers (2000, p. 77) explains that the development of a concept generalizes reality. The concept is thus located on another level than reality. This is the domain of abstraction. In algebra, abstraction is mostly related to generalization.
Generalizing
To generalize is to draw valid conclusions, true in all cases, from the observation and analysis of a few examples (adapted from Squalli, 2002, p. 9). It is to reason by generalization, going from the particular to the general. Generalizing '… is particularly important, because in humans it is the basis for the acquisition of concepts and the possibility of abstraction' (Raynal and Rieunier, 2003, p. 156). Generalization is therefore at the heart of mathematical activity. In algebra, it allows the development of the student's algebraic thinking.
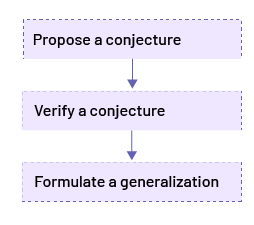
To make a generalization, students observe and analyze situations and then propose conjectures. When proposing a conjecture, students must be able to express their reasoning in their own words. By supporting their conjectures with concrete and visual (semi-concrete) representations and mathematical arguments, students must then verify whether their conjecture is valid in other situations. This process, sometimes informal, helps students learn to formulate their generalizations more clearly.
A conjecture is the expression of an idea that is perceived to be true in any similar situation.
Example
Students analyze the relationship between the position number in the pattern below and the number of squares in the term. One student proposes a conjecture that the number of squares in each term is always two more than in the previous one. Another student mentions that the number of squares is always twice the position number.

To verify the conjecture, the first student can check that Position 2 has two more squares than Position 1 and Position 3 has two more squares than Position 2. This conjecture allows the student to predict that Position 4 will have 2 more squares than Position 3, or 8 squares. The student can verify this by building Position 4. In this case, the reasoning is additive.
The second student can verify their conjecture by checking that Position 1 has 1 group of two squares, Position 2 has 2 groups of two squares and Position 3 has 3 groups of two squares. This reasoning allows the student to predict that in Position 4, there will be 4 groups of two squares (8 squares) and that Position 5 will have 20 groups of two squares, (40 squares). The construction of Position 4 and other subsequent positions will support this conjecture. Note that conjectures must be revised if a counterexample is discovered.
Recognizing that their conjecture seems to apply to all similar situations in a given context, students can formulate their generalization (rule) using words or symbols. In the previous example, the first student formulates his generalization by saying, 'The number of squares that make up a position is always 2 more than the number of squares in the previous position.' The other student can formulate their generalization (rule) verbally or symbolically using the equation s = n × 2, where n represents the position number and s is the number of squares that make it up.
Operating on Unknown Quantities
Operating on unknown quantities is the action of analyzing and acting on what is unknown. 'It is reasoning analytically, thinking about operations, generalizations, not objects (adapted from Squalli & Theis, 2005).' (Ontario Ministry of Education, 2008a, p. 11). According to several researchers, this is what distinguishes algebra from arithmetic (Driscoll, 1999, p. 1; Squalli, 2002, p. 8). Variables are usually represented symbolically by letters. However, in many situations, they can be represented by other symbols (for example, a square, a question mark, a fill-in-the-blank) or concrete materials. They can also be expressed verbally.
'Algebra begins with the awareness of operations, operations in the broad sense of the word, that is, a series of intellectual acts involving reflection and combination of means in order to obtain a result or solve a problem. It is … presented as a 'generalized arithmetic', as a tool for solving problems more powerful than arithmetic.' (Squalli & Theis, 2005, p. 5).
Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 11.
Students' algebraic thinking develops in conjunction with the development of mathematical skills. Thus, students need to develop the ability to reason and solve problems algebraically and then communicate their algebraic reasoning.
Ability to Reason Algebraically
The ability to reason algebraically allows students to analyse mathematical situations and express mathematical relationships. While arithmetic is generally perceived as a calculation on known numbers or quantities and focused on finding the right answer, algebraic reasoning aims to better understand relationships between numbers and quantities to find an unknown. This is why it is essential to develop the ability to reason algebraically, especially in problem-solving situations.
According to Driscoll (1999, p. 1-19), algebraic reasoning includes the ability to “do and undo”, the ability to create rules to represent relationships between two changing quantities and the ability to formulate generalizations about the properties of arithmetic operations.
“Doing and undoing” is important to the strategy of working backwards when reasoning algebraically. For example, students can make use of the inverse relationships between addition and subtraction and between multiplication and division to reason about an equation. Given the equation Δ + 3 = 11, a student who can work backwards understands that they can think about this situation as 11 – 3 because they know that they had to add 3 to the variable to get 11. Inversely, they know that taking 3 away from 11 must represent the variable. This is algebraic reasoning, since the action is performed based on thought and understanding, not a procedure for which the student cannot explain its meaning.
Creating rules to represent relationships involves making generalizations. For example, in the growing pattern below, the student who reasons algebraically recognizes that at Position 1, there is 1 column of two dots, at Position 2, there are 2 columns of three dots, and so on. Thus, the student can generalize and represent the relationship between the number of dots (d) and the position number (n) with an equation [for example, d = n × (n + 1)].

The ability to generalize properties of arithmetic operations also demonstrates algebraic reasoning (for example, knowing that you can change the order of two numbers you want to add without affecting the sum or that the product of a number and 1 is always equal to the number).
Algebraic reasoning is also distinguished from arithmetic reasoning in the following way. Arithmetic reasoning is more concerned with static situations, whereas algebraic reasoning is more concerned with changing situations. Developing students' algebraic reasoning allows them to see and analyze more encompassing situations and to develop their repertoire of problem-solving strategies.
To stimulate students' algebraic reasoning, teachers can use an existing arithmetic problem and give it an algebraic perspective by adding a changing situation. These situations encourage the search for regularities and relationships, the use of variables, and the expression of justifications, conjectures and generalizations.
The table below highlights the difference between a problem that elicits arithmetic reasoning and a problem that elicits algebraic reasoning.
| Arithmetic Reasoning | Algebraic Reasoning |
|---|---|
|
We work with a static situation. Example This problem presents a static situation. It allows only one answer that msut be determined using arithmetic operations. |
We work with a changing situation. Example
This problem presents a changing situation. It focuses on the study of the pattern rule and the relationship between two changing quantities. |
Through algebraic reasoning, students analyze numbers, symbols, quantities, operations, and then generalize them.
The ability to reason algebraically does not develop in a simple and natural way. Therefore, teachers should walk students through the process by encouraging them to:
- explain their reasoning;
- work backwards;
- analyze the relationships between quantities and organize information to represent a situation in another way;
- make conjectures and generalize.
In learning situations, teachers should ask questions that emphasize algebraic concepts and get students thinking.
- Does it work if I do the same thing with other numbers?
- What changes? What does not change?
- Can I predict the outcome based on the information gathered?
- Can the regularity be applied to any case?
- Do I always follow the same steps? What are they?
Ability to Solve a Problem Algebraically
Problem solving is designed to engage students in a process that requires the use of different strategies. Students who have developed strategies find it easier to initiate the resolution of a problem, to anticipate and predict outcomes, to reason and to find a solution.
A problem-solving situation refers to a problem that:
- is in context;
- allows the use of different strategies;
- is a challenge for the student.
Below is a problem that can be solved arithmetically or algebraically:
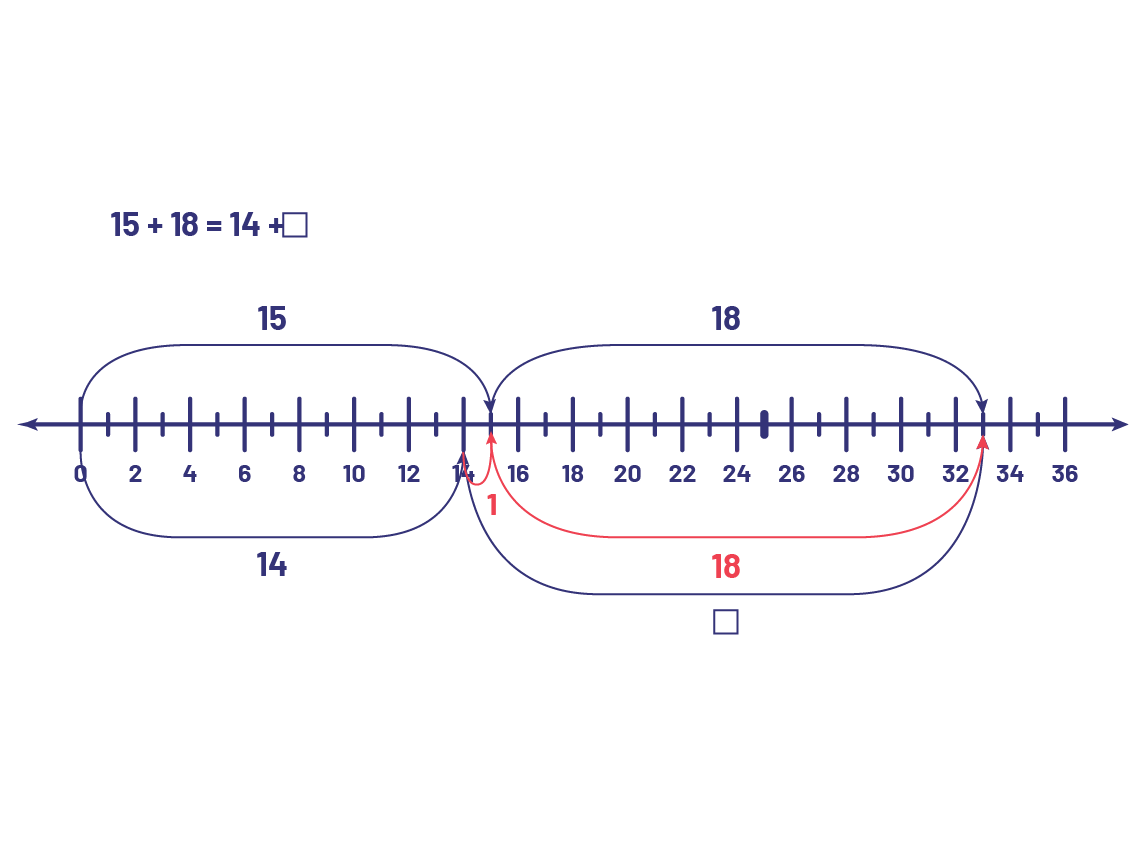
Sylvia has 15 red fish and 18 yellow-striped fish. Jacob has the same number of fish, but only 14 of his fish are red. How many yellow-striped fish does Jacob have?

| Solving with Arithmetic Reasoning | Solving with Algebraic Reasoning |
|---|---|
| We perform arithmetic operations to solve the problem. I know that Sylvia has 33 fish in total, because 15 plus 18 is 33. 15 + 18 = 33 Jacob has the same number of fish. So if he has 14 red fish, he must have 19 fish with yellow stripes, because 33 minus 14 is 19. 33 – 14 = 19 |
Instead of doing calculations, we interpret the problem and compare the quantities. We can represent the situation with an equation. To solve it, we compare the quantities on either side of the '=' sign. I know that Sylvia and Jacob have the same number of fish. 15 + 18 = 14 + □ If Sylvia has 15 goldfish and Jacob has 14, then Jacob has 1 less goldfish than Sylvia.  Since Jacob has the same number of fish as Sylvia, he must have 1 more yellow-striped fish than Sylvia . 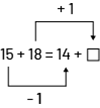 Therefore □ = 19. |
In general, students tend to solve such a problem arithmetically. Teachers can then vary the parameters of the problem by giving it an algebraic perspective, for example, by asking students to represent the problem using an equation. To solve the equation, students can use a number line, which can help them think about the mathematical situation. The important thing is to understand the relationship of equality between the two numerical expressions, not to do the calculation.
Ability to Communicate Algebraic Reasoning
Communication benefits everyone involved in the exchange. The obligation to share one's understanding of a situation or concept often contributes to the improvement or deepening of that understanding.
The ability to communicate algebraic reasoning is developed when students express their understanding of a problem or concept and defend their ideas using different representations:
- the concrete mode, linked to exploration, manipulation and creation using concrete materials;
- the visual (semi-concrete) mode, linked to a picture, a drawing or any other representation on paper;
- the symbolic mode, linked to any representation made from numbers or symbols;
- the 'with words' mode, linked to an explanation or a verbal or written description.
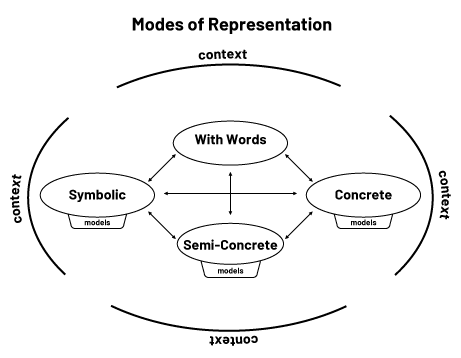
In order to develop a solid understanding, students need to have experiences in context by exploring problem situations. Contextualization allows students to make connections between various representations and to develop an understanding of the algebraic concepts being explored. Teachers also use a variety of representations to help students take ownership of mathematical concepts, make connections between representations, facilitate transfer, and elicit cognitive flexibility in relation to the concepts.
Mathematical argumentation is an essential tool for communication in mathematics. Students need to be able to justify their representations, ideas, and understanding using mathematical arguments and a vocabulary of causal relationships (for example, if… therefore, because, since). Mathematical arguments allow students to present their understanding in a much more accurate and thoughtful way. A mathematical argument is a verbal or written justification of a reasoning to demonstrate or refute a mathematical idea.
Exchanging ideas allows students to communicate mathematical representations and arguments. When solving a problem in algebra, students formulate conjectures, present their possible solutions, compare their ideas or justify their results using different representations. In short, students communicate.
Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 18.
The components of algebra learning are the fundamental elements that learning in algebra should address, regardless of grade (National Council of Teachers of Mathematics, 2000, pp. 37-40). These components are part of the foundation of the curriculum. In algebra, the goal is to advance students' learning by having them understand relationships, use mathematical models to understand and analyze change, and represent problems using symbols.
Each of these components is discussed below. Then, a problem is analyzed to illustrate the integration of these components in the learning of algebra.
Understanding Patterns and Relationships
Understanding relationships is an important problem-solving skill in algebra, as it supports the acquisition of concepts and the formulation of conjectures leading to generalizations. When students perceive and describe patterns, compare, represent, and create situations or patterns based on regularities, they are on their way to establishing relationships between quantities.
In the Junior Division, students explore relationships between changing quantities, particularly in situations involving growing patterns. To develop their sense of symbol, students observe, analyze, and represent numbers in number sentences and equations.
Use of Mathematical Models
The ability to use models is an integral part of the Mathematics Curriculum. Mathematical models are used to represent situations in order to analyze the relationships between numbers and quantities. Over time, mathematicians have created, used, and generalized certain ideas, strategies, and representations to facilitate the understanding of concepts. In use, some representations have become accepted models, such as the number line and the array. It is important for students to use different models in a variety of activities so that they can move easily from one representation to another.
Example
The 3 × 4 multiplication is represented here in three different ways.
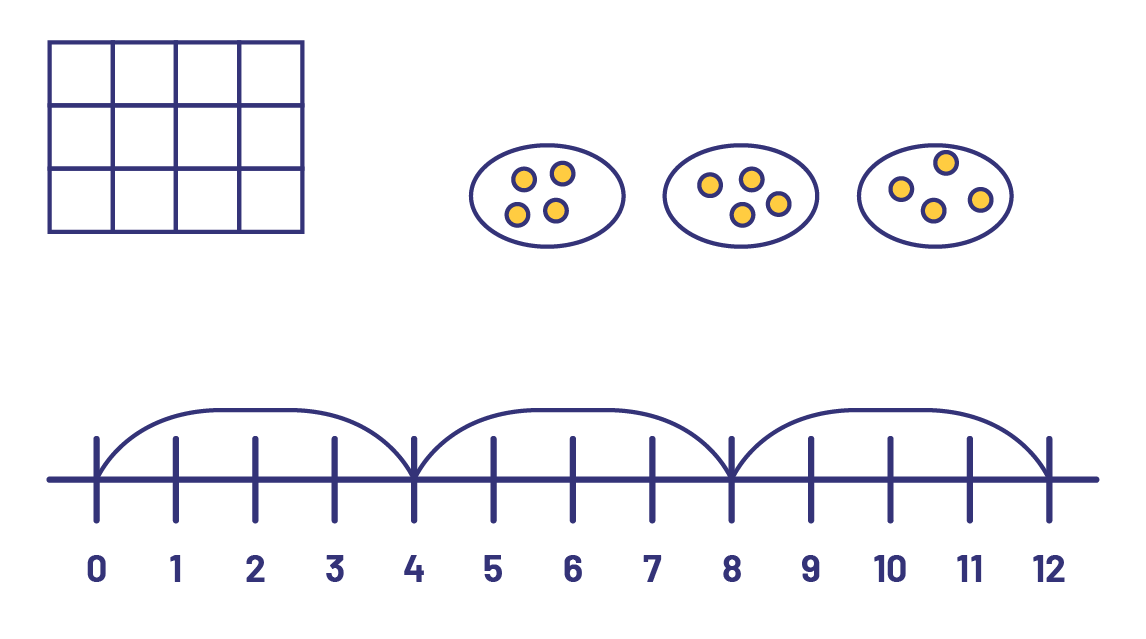
When faced with a problem, several representations are possible; a number of students use their bodies, manipulatives or drawings, while others represent the data more schematically. The way in which the data is represented and organized using models reflects the degree of development of algebraic thinking.
According to Fosnot and Dolk (2001), models, like big ideas and strategies, cannot be transmitted automatically; students must construct them themselves in order to internalize them. It is therefore important to present them with problems that are conducive to modelling, so that students create their own symbols and models to represent situations, instead of systematically proposing the usual algorithms or learned strategies.
To help students reason, teachers should offer a variety of models and representations, and encourage students to use them frequently.
In representing a problem, students analyze relationships using models, draw conclusions, and explain them using words. Models are tools that support students in noticing and naming relationships and therefore develop algebraic thinking. They promote analysis and introduce students to a level of abstraction that facilitates making predictions and generalizations. Dialogue, sharing ideas about the data in the problem represented by different models, and questions from the teacher are all ways to engage students in thinking.
Understanding Change
Students live in a changing world. Understanding that change is a part of life and that most things change over time (for example, each year their height and weight increases and their feet grow in length) is an important aspect of algebraic thinking.
Observed changes can be described qualitatively (for example, I am taller than last year; my hair is longer; the bucket filled with water quickly during the storm; it is colder now than this morning) and quantitatively (for example, I grew 2 cm this year; the bucket of water filled with 50 mL in 30 minutes; the temperature dropped 6°C in 3 hours).
Students learn to observe and understand change in patterns, in equivalent relationships and in problems.
Change and regularities are two inseparable concepts in exploring the relationships between two changing quantities. Students realize that the change in one quantity affects another. For example, by looking at the growing pattern below, students can recognize the change from one position to the next, and that the number of squares increases from one position to the next. As they investigate the change further, students can recognize that the number of squares doubles with each position.

Students may even find that the number of squares that make up a position is equal to 2 × 2 × 2 × … × 2, where the multiplier equals the position number × 2 doubled, or the position number × 4.
The study of a changing quantity is a major leap in the way we see things. For example, in a problem that involves the lengths 5 cm, 7 cm, 9 cm…, instead of seeing several quantities, we consider that it is a single length that is changing, hence the need to involve the concept of the variable.
Example of Integrating the Components in a Problem-Solving Situation
The representation of problems using symbols is a fundamental component of algebraic thinking. It is important to move students toward a more abstract and formal representation of situations using symbols; in this way, students develop their symbolic literacy.
Example of integrating the components in a problem situation
The following example illustrates the integration of algebraic reasoning into a problem-solving situation.
In the city where Jessie and Boukar live, there are two Fitness Centres, Mega and Extra, which offer different plans for their members.
Jessie goes to the Mega Fitness Centre, where the membership cost is $25 and classes cost $2 each.
Boukar has a subscription to the Extra Fitness Centre, where the cost of the membership is $4 and classes cost $5 each.
Using this information, determine when Jessie and Boukar will have paid the same amount of money for the same number of classes.
After presenting the problem, teachers can ask questions and invite students to complete various tasks to integrate algebraic reasoning.
Understanding Patterns and Relationships
Teachers can highlight patterns and relationships by inviting students to represent the patterns in the different scenarios using concrete materials or a model.
In general, students should note that at the Mega Fitness Centre, the amount paid increases by $2 each time Jessie takes a class, while at the Extra Fitness Centre, it increases by $5 each time Boukar takes a class. By further analyzing the situation, students can recognize that there is a relationship between the amount paid and the number of classes taken at each Fitness Centre.
Use of Mathematical Models
Models that can be used to explore this problem include:
Number Line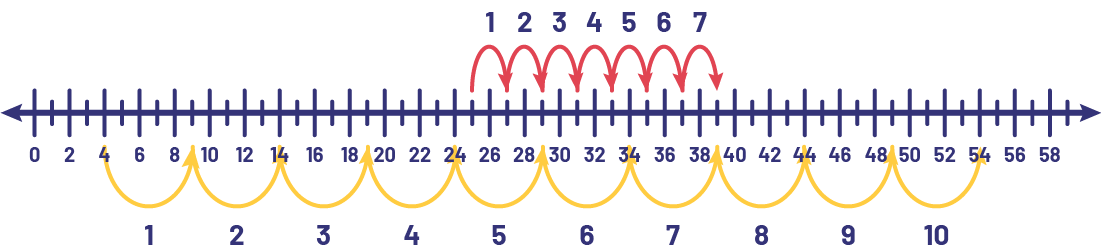 |
||||||||||||||||||||||||||||||||||||||||||||||||
Manipulatives
 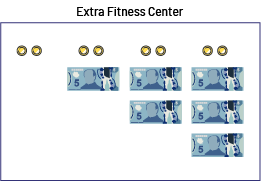 |
||||||||||||||||||||||||||||||||||||||||||||||||
Table of values Mega Fitness Centre
Extra Fitness Centre
|
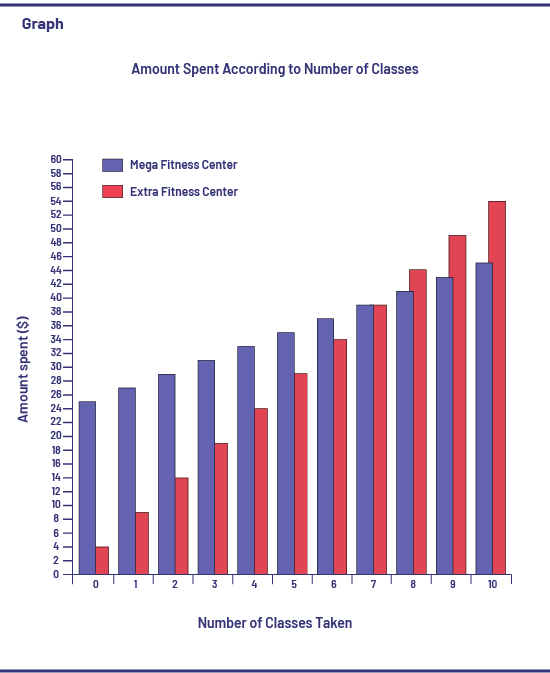
Understanding Change
Here are some questions that can be asked to analyze the change in this problem:
- What information allows you to predict (extrapolate) what will happen?
- What step or steps must be repeated to find the amount spent?
- When different numbers are used, what changes? What doesn't change?
- How does this representation (for example, with the manipulatives) resemble this one (for example, the table of values)?
- Would this approach still work with other numbers? How do you know?
Represent Problem-Solving Situations Using Symbols
By offering strategic feedback, teachers can assist students to represent the situation using symbols.
Examples
At the Mega Fitness Centre: s = 2 × c + 25, where s is the amount spent and c is the number of classes.
At the Extra Fitness Centre: s = 5 × c + 4, where s is the amount spent and c is the number of classes.
Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 20-27.
Teachers are vital in the development of algebraic thinking in the classroom. The teacher's role is not defined solely by the choice of tasks, but also by their teaching moves, which aim to encourage students to go beyond arithmetic reasoning and to access a symbolic way of thinking. Doing mathematics thus takes on its full meaning.
Some authors (for example, Blanton & Kaput, 2003, pp. 70-77) believe that teachers need 'algebraic eyes and ears' to identify and maximize connections to algebraic concepts in mathematical activities and to take advantage of opportunities to develop students' algebraic thinking.
To do this, the teacher can:
Vary the parameters of a problem
Use an existing problem and give it an algebraic perspective, by promoting the search for relationships, patterns, conjectures and generalizations.
For example consider the following problem typically associated with the Numbers strand:
In a team of four people, how many handshakes will there be if each person shakes hands with all the other people only once?
The teacher could use this problem and ask questions that draw out connections to algebraic concepts, such as:
- How many handshakes will there be if one, two or three other people are added to the team?
- Organize the data in a table of values. Do you see a pattern?
- How many handshakes will there be if ten people are added to the team?
Ask questions to help students generalize
- What can be said about the relationship between the number of people on the team and the total number of handshakes?
- Is there a regularity? Explain your answer.
Ask questions with an emphasis on algebraic concepts
- Can you explain the problem in your own words?
- Can you solve the problem using another representation?
- How do we make sure that this solution is true?
- Would this approach work with other numbers? Always?
- What changes?
- What does not change?
These questions encourage students to make conjectures and explain them with mathematical arguments.
Develop and strengthen a symbol literacy
Teachers should understand that symbol literacy is an important concept for students and to support them in its development. Too often, the application of mathematical symbols is done automatically, with students perceiving these symbols simply as a command to perform a mathematical operation. Students can then have difficulty solving a problem correctly and explaining the meaning of the number sentence they have written because they do not understand the symbols used in it. The teacher should be mindful of supporting students to:
- read the symbols and think about what they represent before acting;
- understand the correct meaning of mathematical symbols (for example, the '=' sign represents a relationship between the numerical expressions on either side of the sign and is not a precursor to the answer);
- recognize and use symbols as communication tools to interpret a mathematical sentence and to express reasoning.
Creating an 'algebraic' learning environment
An 'algebraic' learning environment is one where the development of analytical thinking is emphasized. Teachers consciously identify times when reasoning is an integral part of their instruction. Arguing, abstracting, and generalizing become common practice during daily lessons in mathematics and even in other subjects, not an occasional enrichment.Creating an 'algebraic' learning environment means giving students the chance to experience the world around them with 'algebraic' eyes and ears, be able to generalize explicitly.
Source: translated from Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, p. 23-24.