Fondements généraux du domaine Algèbre
Cycle moyen
Introduction
« Le domaine Algèbre est une composante qui prend de plus en plus d’importance dans l’évolution des mathématiques. Chaque jour, nous sommes confrontés à une multitude de problèmes composés d’une variété d’inconnues. C’est en essayant de voir des patrons, des régularités, que des solutions seront trouvées. » (Ministère de l’Éducation de l’Ontario, 2000, p. 15)
Le domaine Algèbre regroupe des concepts essentiels aux mathématiques pour représenter et analyser des relations que l’on trouve dans plusieurs situations de la vie courante.
L’étude de l’algèbre s’est développée à partir du besoin de comprendre et de représenter le monde réel, par exemple, la position des planètes, le mouvement des marées, le déplacement des objets en chute libre. Les spécialistes des mathématiques ont tenté de résoudre ces questions par l’observation des régularités et la modélisation des phénomènes par des équations et des représentations graphiques. Ces travaux ont contribué au développement de symboles mathématiques et de méthodes de calcul. Or, « dans ce nouveau millénaire, l’algèbre n’est plus une discipline qui s’attarde à la manipulation de symboles. L’algèbre devient un mode de pensée, une façon de voir et d’exprimer des relations. » (Ministère de l’Éducation de l’Ontario, 2000, p. 26)
Au cycle moyen, les élèves observent les changements dans le monde qui les entoure, les décrivent et les représentent d’abord de façon concrète et semi-concrète, puis de façon symbolique.
Par exemple, la suite croissante ci-dessous est utilisée afin de représenter une situation. Les élèves apprennent à décrire la régularité que l’on peut voir d’un rang à l’autre, à exprimer la relation entre le rang et le nombre de cubes qui le composent et à représenter cette relation par une table de valeurs et par une équation.
 image Suite croissante non numérique de cubes. Rang un : un cube violet et 2 cubes rouges. Rang 2 : un cube bleu, 2 cubes rouges et 2 cubes verts. Rang 3 : un cube bleu, 2 cubes rouges, 2 cubes verts et 2 cubes orange. Rang 4 : un cube bleu, 2 cubes rouges, 2 cubes verts, 2 cubes orange et 2 cubes violets.
image Suite croissante non numérique de cubes. Rang un : un cube violet et 2 cubes rouges. Rang 2 : un cube bleu, 2 cubes rouges et 2 cubes verts. Rang 3 : un cube bleu, 2 cubes rouges, 2 cubes verts et 2 cubes orange. Rang 4 : un cube bleu, 2 cubes rouges, 2 cubes verts, 2 cubes orange et 2 cubes violets.Les élèves observent qu’il y a une constante (+1), soit le cube bleu qui ne change pas d’un rang à l’autre.
Les élèves observent également la relation entre le numéro indiquant le rang et le nombre de cubes afin d’en arriver à une règle : nombres de cubes = numéro du rang × 2 + 1. Dans ce cas, c’est une règle composée d’un multiplicateur (partie qui fait croître la suite) et d’une constante. Cette règle leur permet de faire des prédictions lointaines.
La pensée algébrique
Aux cycles primaire et moyen, le domaine Algèbre a pour but principal de développer chez les élèves la pensée algébrique. Dans la recherche d’une définition de ce qu’est la pensée algébrique, plusieurs auteures et auteurs privilégient une perspective jugée essentielle en algèbre.
En voici trois exemples qui reflètent trois perspectives différentes :
« L’algèbre est quelquefois définie comme la généralisation de l’arithmétique ou comme un langage pour généraliser l’arithmétique. Mais l’algèbre, c’est plus qu’un ensemble de règles pour manipuler des symboles, c’est une manière de penser. » [traduction libre] (Vance, 1998, p. 282)
« L’algèbre est un langage. Ce langage comprend entre autres : les relations, les inconnues et les variables, ainsi que la généralisation des régularités. Chaque fois qu’une de ces idées est discutée, que ce soit à la maternelle ou à un autre niveau, c’est une occasion de travailler le langage de l’algèbre. » [traduction libre] (Usiskin, 1997, p. 346)
« L’algèbre peut être un outil puissant pour résoudre des problèmes. Elle permet d’accéder à des solutions beaucoup plus facilement. […] Elle peut devenir un outil indispensable pour représenter et résoudre des situations complexes du monde qui nous entoure. » [traduction libre] (Baroody et Coslick, 1998, p. 16-3)
Parmi les nombreux éléments qui contribuent à l’efficacité de l’enseignement en Algèbre, certains ont une incidence plus grande sur le développement de la pensée algébrique. Ainsi, il est important de reconnaître particulièrement les éléments suivants :
- les processus fondamentaux pour accéder à des niveaux d’abstraction supérieurs (abstraire, généraliser et opérer sur l’inconnue);
- les habiletés mathématiques développées selon une perspective algébrique (résoudre un problème, raisonner et communiquer);
- les composantes de l’apprentissage de l’algèbre (comprendre des relations, représenter à l’aide de symboles, utiliser des modèles et analyser le changement);
- les concepts algébriques regroupés selon une grande idée (relations).
L’affiche ci-dessous illustre l’interaction entre ces éléments.
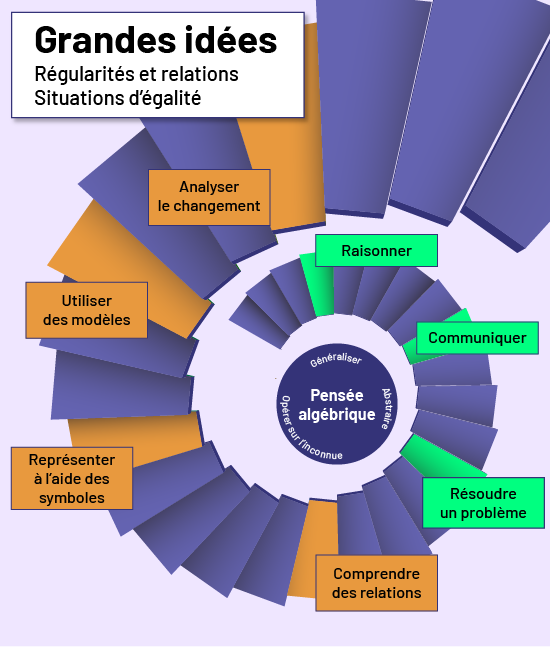 image Grandes idées. Modèles et relations. Situations d'égalité. Un escalier en colimaçon descendant avec les mots suivants qui descendent en spirale avec l'escalier: analyser le changement, utilisation de modèles, représentations à l'aide de symboles, comprendre les relations, résoudre un problème, communiquer, raisonner. Au bas de l'escalier en colimaçon, il y a un cercle avec les mots suivants à l'intérieur : pensée algébrique, généraliser, abstrait, opérer sur une inconnue.
image Grandes idées. Modèles et relations. Situations d'égalité. Un escalier en colimaçon descendant avec les mots suivants qui descendent en spirale avec l'escalier: analyser le changement, utilisation de modèles, représentations à l'aide de symboles, comprendre les relations, résoudre un problème, communiquer, raisonner. Au bas de l'escalier en colimaçon, il y a un cercle avec les mots suivants à l'intérieur : pensée algébrique, généraliser, abstrait, opérer sur une inconnue. Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 5-8.
Concepts algébriques regroupés selon une grande idée
« Lorsque les enseignantes et les enseignants disposent d’un programme-cadre structuré, axé sur les concepts essentiels en mathématiques et, en outre, fondé sur les grandes idées, ils peuvent déterminer la composition de leçons susceptibles de favoriser l’apprentissage de ces concepts mathématiques importants. » (Ministère de l’Éducation de l’Ontario, 2004a, p. 21)
Les attentes et les contenus d’apprentissage en algèbre font appel à un grand nombre de concepts. Le regroupement de ces concepts sous de grandes idées favorise la planification d’une programmation plus efficace de l’enseignement. Ce faisant, le personnel enseignant est en mesure d’élaborer des situations d’apprentissage cohérentes qui permettent aux élèves :
- d’explorer les concepts en profondeur;
- d’établir des liens entre ces concepts;
- de développer une pensée algébrique.
Une grande idée est l’énoncé d’une idée fondamentale pour l’apprentissage des mathématiques, une idée qui lie de nombreuses connaissances mathématiques en un tout cohérent.
« L’un des thèmes les plus importants des mathématiques est l’étude des régularités et des relations. […] L’accent de l’enseignement se déplace de l’exploration des régularités à celles des relations. Quand les élèves utilisent des graphiques, des tables de valeurs, des expressions, des équations ou des descriptions verbales pour représenter une relation, ils voient plus facilement différents aspects d’une situation. Grâce à ces activités, les élèves développent une compréhension des concepts d’inconnue et de variable, et des effets des changements d’une variable sur une autre. »
(Ministère de l’Éducation de l’Ontario, 2005, p. 10)
La grande idée de relations constitue la base des attentes du domaine Algèbre de la 4e à la 6e année. Cette grande idée place la compréhension des relations entre des quantités ou des nombres au centre de tous les apprentissages en algèbre. Son développement en fonction des deux énoncés qui la sous-tendent, soit l’exploration de relations et le sens du symbole, aide le personnel enseignant à définir et à prioriser les concepts clés, et à mettre en œuvre des stratégies d’enseignement efficaces et cohérentes.
Grande idée 1 : Relations
La compréhension des relations entre des quantités ou des nombres dans des situations mathématiques avec ou sans contexte constitue la base de la pensée algébrique.
Énoncé 1 - Exploration de relations
L’analyse de situations impliquant des quantités en changement dans le but d’établir la relation entre ces quantités favorise le développement de la pensée algébrique.
Énoncé 2 - Sens du symbole
Le sens du symbole permet d’interpréter diverses relations mathématiques et de représenter un raisonnement algébrique.
Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 27-30.
Dans une classe de mathématiques visant à développer la pensée algébrique chez les élèves, l’objectif traditionnel de l’enseignement, apprendre à calculer, n’est pas omis; il est largement dépassé. Développer la pensée algébrique est un cheminement complexe qui mise sur trois processus fondamentaux : abstraire, généraliser et opérer sur l’inconnue.
Abstraire
Faire abstraction de, c’est « écarter par la pensée, ne pas tenir compte de » (Le nouveau Petit Robert, 2006, p. 11). L’abstraction est une des caractéristiques de la pensée algébrique. Au cycle primaire, les élèves apprennent que peu importe les objets en question, deux objets plus deux objets donnent quatre objets. Pour comprendre ce concept, les élèves ne tiennent pas compte des objets en soi, mais se concentrent sur leur nombre. Abstraire, c’est se détacher de l’aspect sensoriel des choses pour raisonner à un niveau plus général (adapté de Raynal et Rieunier, 2003, p. 13), c’est se représenter mentalement une situation concrète, c’est passer à un niveau de conceptualisation plus profond. Piaget considère l’abstraction comme un des processus de base de la construction des savoirs. Pour sa part, Roegiers (2000, p. 77) explique que l’appropriation d’un concept généralise la réalité. Le concept se situe donc sur un autre plan que la réalité. C’est là le domaine de l’abstraction. En algèbre, l’abstraction est surtout reliée à la généralisation.
Généraliser
Généraliser, c’est tirer des conclusions valables, vraies dans tous les cas, à partir de l’observation et de l’analyse de quelques exemples (adapté de Squalli, 2002, p. 9). Il s’agit de raisonner par généralisation, en allant du particulier au général. Généraliser « […] est particulièrement important, car chez l’homme, il est à la base de l’acquisition des concepts et des possibilités d’abstraction » (Raynal et Rieunier, 2003, p. 156). La généralisation est alors au cœur de l’activité mathématique. En algèbre, elle permet de développer la pensée algébrique de l’élève.
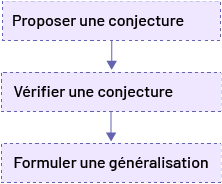
Pour arriver à une généralisation, les élèves observent et analysent des situations pour ensuite proposer des conjectures. Au moment de proposer une conjecture, les élèves doivent être en mesure d’exprimer leur raisonnement dans leurs mots. En appuyant leurs conjectures au moyen de représentations concrètes et semi-concrètes et d’arguments mathématiques, les élèves doivent ensuite vérifier si leur conjecture est valable dans d’autres situations. Ce processus, parfois informel, permet aux élèves d’apprendre à formuler plus clairement leurs généralisations.
« Une conjecture est l'expression d'une idée percue comme étant vraie dans toute situation semblable. » (Ministère de l’Éducation de l’Ontario, 2008, p.10)
Exemple
Les élèves analysent la relation entre le numéro indiquant le rang des figures dans la suite ci-dessous et le nombre de carrés qui les composent. Un élève propose une conjecture, soit que le nombre de carrés dans chaque figure est toujours deux de plus que dans la figure précédente. Un autre élève mentionne que le nombre de carrés est toujours deux fois le numéro indiquant le rang.
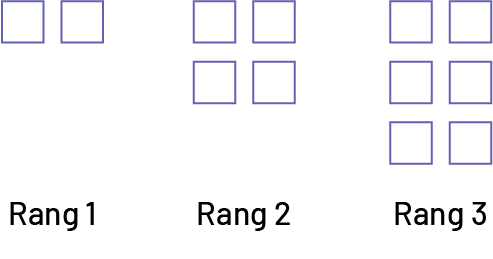
Pour vérifier sa conjecture, le premier élève peut vérifier qu’au rang 2 la figure a bien 2 carrés de plus que la figure au rang 1 et que la figure au rang 3 a bien 2 carrés de plus que la figure au rang 2. Sa conjecture l’autorise à prédire qu’à la figure au 4e rang, il y aura 2 carrés de plus que 6, soit 8 carrés, et l’élève peut le vérifier en construisant la figure au 4e rang. Dans ce cas, il s’agit d’un raisonnement additif.
Le deuxième élève peut vérifier sa conjecture en vérifiant qu’à la figure au rang 1, il y a 1 groupe de 2 carrés, qu’au rang 2, il y a 2 groupes de 2 carrés et qu’au rang 3, il y a 3 groupes de 2 carrés. Cette conjecture/relation lui permet de prédire qu’au 4e rang, il y aura 4 groupes de 2 carrés (soit 8 carrés) et que la figure au rang 20 aura 20 groupes de 2 carrés, soit 40 carrés. La construction de la figure au 4e rang et d’autres figures subséquentes permettent d’appuyer sa conjecture. Notons que la conjecture doit être revue si on découvre un contre-exemple.
Reconnaissant que leur conjecture semble s’appliquer à toutes les situations similaires dans un contexte donné, les élèves formulent leur généralisation (la règle) en ayant recours à des mots ou à des symboles. Dans l’exemple précédent, le premier élève formule sa généralisation en disant : « Le nombre de carrés qui composent une figure est toujours 2 de plus que le nombre de carrés du rang précédent. » L’autre élève peut formuler sa généralisation (la règle) à l’oral ou de façon symbolique au moyen de l’équation n = r × 2, où r est le rang et n, le nombre de carrés qui la composent.
Opérer sur l’inconnue
Opérer sur l’inconnue, c’est traiter et examiner ce qui est inconnu. C’est raisonner de manière analytique, c’est réfléchir sur les opérations, les généralisations et non sur les objets (adapté de Squalli et Theis, 2005). Selon plusieurs chercheurs, c’est ce qui distingue l’algèbre de l’arithmétique (Driscoll, 1999, p. 1; Squalli, 2002, p. 8). Les variables sont généralement représentées de façon symbolique par des lettres. Toutefois, dans bien des situations, elles peuvent l’être par d’autres symboles (par exemple, un carré, un point d’interrogation, un trait à remplir) ou du matériel concret. Elles peuvent aussi être exprimées oralement.
L’algèbre commence par la prise de conscience des opérations, opérations dans le sens large du mot, c’est-à-dire une série d’actes intellectuels supposant réflexion et combinaison de moyens en vue d’obtenir un résultat ou de résoudre un problème. L’algèbre est « […] présentée comme une “arithmétique généraliséeˮ, comme un outil de résolution de problèmes plus puissant que l’arithmétique » (Squalli et Theis, 2005, p. 5).
Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 9-11.
« Raisonner à l’aide de concepts et de processus mathématiques ne peut logiquement se faire que si l’on communique avec le langage mathématique, et le raisonnement mathématique s’exerce le plus généralement en situation de résolution de problèmes. » (Ministère de l’Éducation du Québec, 2001, p. 125)
La pensée algébrique des élèves se développe en relation avec le développement d’habiletés mathématiques. Ainsi, les élèves doivent développer leur habileté à raisonner et à résoudre des problèmes de façon algébrique, puis à communiquer leur raisonnement algébrique.
Habileté à raisonner de façon algébrique
L’habileté à raisonner de façon algébrique permet aux élèves d’examiner des situations et d’organiser leur pensée. Alors que l’arithmétique est généralement perçue comme un calcul sur des quantités connues, misant à trouver la bonne réponse, le raisonnement algébrique vise à mieux comprendre la numération en permettant d’analyser les relations entre les nombres pour trouver une valeur inconnue. C’est pourquoi il est primordial de développer, à l’élémentaire, l’habileté à raisonner de façon algébrique, plus particulièrement dans des situations de résolution de problèmes.
Selon Driscoll (1999, p. 1-19), le raisonnement algébrique inclut l’habileté à « faire et défaire », l’habileté à créer des règles pour représenter des relations entre deux quantités en changement et l’habileté à formuler des généralisations au sujet des propriétés des opérations arithmétiques.
L’habileté à « faire et défaire » se manifeste lorsque les élèves réussissent à procéder à rebours. Par exemple, les élèves peuvent faire appel aux liens entre l’addition et la soustraction et entre la multiplication et la division. Étant donné l’équation Δ + 3 = 11, l’élève qui peut procéder à rebours comprend que l’on peut soustraire 3 de la somme (11 – 3 = 8) pour déterminer la valeur inconnue, car on a ajouté 3 à la variable pour obtenir une somme de 11. Il s’agit d’un raisonnement algébrique, puisque l’action est effectuée en fonction d’une réflexion et d’une compréhension, et non d’une procédure pour laquelle l’élève ne peut en expliquer le sens.
L’habileté à créer des règles pour représenter des relations fait appel à l’habileté à généraliser à partir de règles. Par exemple, dans la suite croissante ci-dessous, l’élève qui raisonne algébriquement peut d’abord reconnaître qu’au rang 1, la figure est composée de 1 colonne de 2 points, qu’au rang 2, la figure est composée de 2 colonnes de 3 points… Ainsi, l’élève peut généraliser et représenter la relation entre le nombre de points (p) et le rang (r) par une équation [par exemple, p = r × (r + 1)].
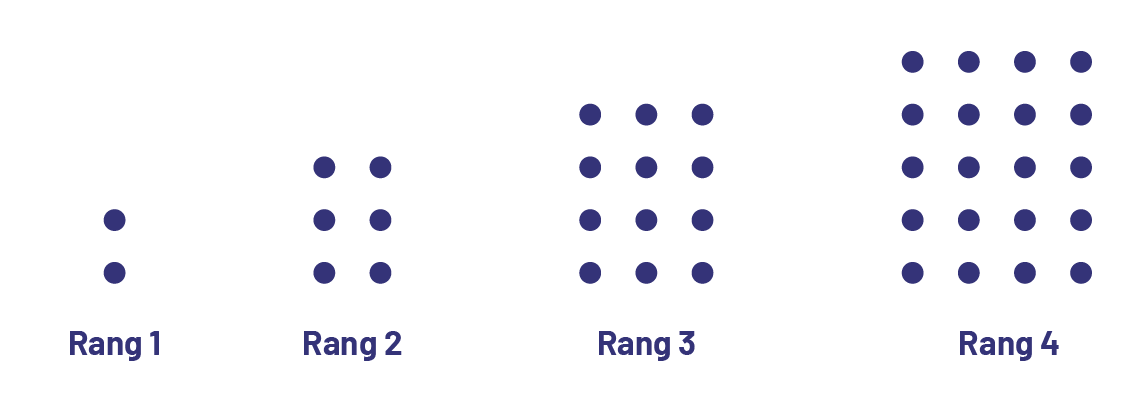
L’habileté à généraliser les propriétés des opérations arithmétiques démontre aussi un raisonnement algébrique (par exemple, savoir que l’on peut changer l’ordre de deux nombres que l’on veut additionner sans affecter la somme ou que le produit d’un nombre et de 1 est toujours égal au nombre).
Le raisonnement algébrique se distingue aussi du raisonnement arithmétique de la façon suivante. Le raisonnement arithmétique porte plutôt sur des situations statiques, alors que le raisonnement algébrique porte davantage sur des situations en changement. En développant le raisonnement algébrique des élèves, on leur permet de voir et d’analyser des situations plus englobantes et de développer leur répertoire de stratégies de résolution de problèmes.
Pour stimuler le raisonnement algébrique des élèves, le personnel enseignant peut utiliser un problème arithmétique existant et lui donner une perspective algébrique en ajoutant une situation en changement. Ces situations favorisent la recherche de régularités et de relations, l’utilisation de variables ainsi que l’expression de justifications, de conjectures et de généralisations.
Le tableau ci-dessous fait ressortir la différence entre un problème qui suscite un raisonnement arithmétique et un problème qui suscite un raisonnement algébrique.
| Raisonnement arithmétique | Raisonnement algébrique |
|---|---|
On travaille à partir d’une situation statique. Exemple Ce problème présente une situation statique. Il admet une seule réponse qu’il faut déterminer à l’aide d’opérations arithmétiques. | On travaille à partir d’une situation en changement. Exemple
Ce problème présente une situation en changement. Il porte sur l’étude de règle de régularité et surtout de règle de correspondance (relation entre deux quantités en changement). |
En raisonnant algébriquement, les élèves analysent les nombres, les symboles, les quantités et les opérations, puis généralisent.
Voici un autre exemple où on peut observer la différence entre un raisonnement algébrique et un raisonnement arithmétique.
Dans l’image ci-dessous, il y a le même nombre de carrés de chaque côté de la flèche. Combien de carrés y a-t-il sous la cloche?
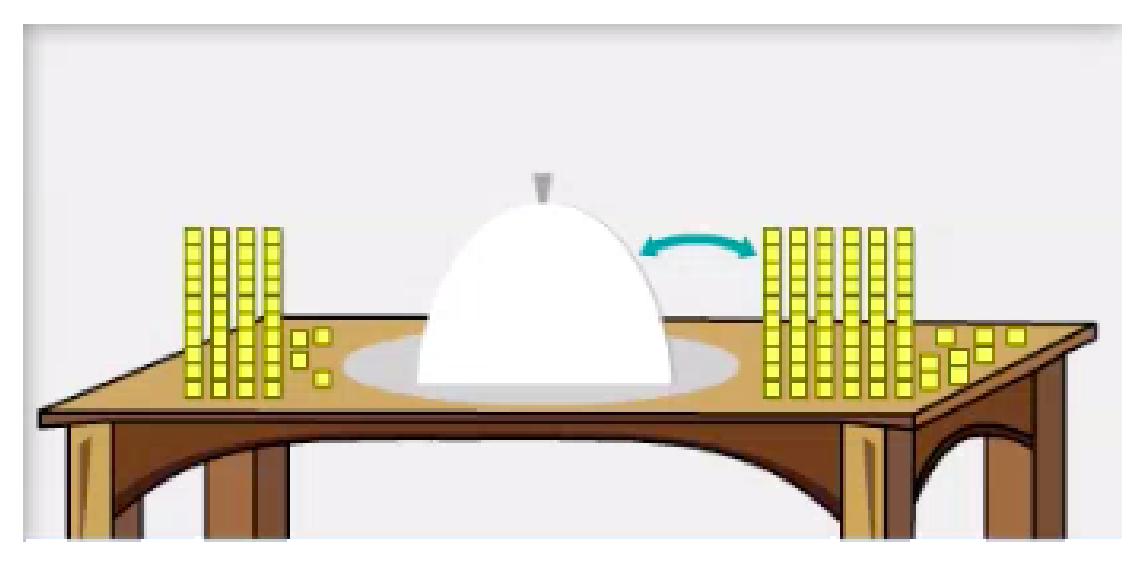 image Exemple de raisonnement algébrique et arithmétique d'un tableau comportant des carrés des deux côtés. Le côté droit à 6 colonnes de dix carrés jaunes et 8 carrés jaunes sur le côté. Le côté gauche a 4 colonnes de dix carrés jaunes et 4 carrés jaunes sur le côté. Une flèche bleue part des carrés jaunes et se dirige vers la cloche située au milieu du tableau.
image Exemple de raisonnement algébrique et arithmétique d'un tableau comportant des carrés des deux côtés. Le côté droit à 6 colonnes de dix carrés jaunes et 8 carrés jaunes sur le côté. Le côté gauche a 4 colonnes de dix carrés jaunes et 4 carrés jaunes sur le côté. Une flèche bleue part des carrés jaunes et se dirige vers la cloche située au milieu du tableau.Cliquer sur l’image pour constater la différence entre les deux raisonnements.
Source : L’@telier - Ressources pédagogiques en ligne (atelier.on.ca).
La capacité de raisonner algébriquement ne se développe pas de façon simple et naturelle. C’est pourquoi le personnel enseignant doit faire cheminer les élèves en les incitant :
- à expliciter leur raisonnement;
- à travailler à rebours;
- à analyser les liens entre les quantités et à organiser l’information pour représenter une situation d’une autre façon;
- à proposer des conjectures et à généraliser.
Dans le cadre de situations d’apprentissage, le personnel enseignant doit poser des questions qui mettent l’accent sur des concepts algébriques et qui amènent les élèves à réfléchir.
En voici quelques exemples :
- Est-ce que ça fonctionne si je fais la même chose avec d’autres nombres?
- Qu’est-ce qui change? Qu’est-ce qui ne change pas?
- Est-ce que l’information recueillie me permet de prédire le résultat?
- Est-ce que la régularité peut être appliquée à n’importe quel cas?
- Est-ce que je suis toujours les mêmes étapes? Quelles sont-elles?
Habileté à résoudre une situation-problème de façon algébrique
La résolution d’une situation-problème vise à engager les élèves dans un processus où seront utilisées différentes stratégies. Les élèves qui ont développé des stratégies ont plus de facilité à amorcer la résolution d’une situation-problème, à anticiper et à prédire des résultats, à raisonner et à trouver une solution.
Une situation-problème désigne un problème qui :
- est en contexte;
- permet d’utiliser différentes stratégies;
- représente un défi pour l’élève.
Voici une situation-problème qui peut être résolue de façon arithmétique ou algébrique.
Sylvia a 15 poissons rouges et 18 poissons à rayures jaunes. Jacob a le même nombre de poissons, mais seulement 14 de ses poissons sont rouges. Combien Jacob a-t-il de poissons à rayures jaunes?

| Résolution à l’aide d’un raisonnement arithmétique | Résolution à l’aide d’un raisonnement algébrique |
|---|---|
| Je sais que Sylvia a 33 poissons en tout, car 15 plus 18, c’est 33. 15 + 18 = 33 Jacob a le même nombre de poissons. Alors s’il a 14 poissons rouges, il en a 19 qui ont des rayures jaunes, car 33 moins 14, c’est 19. 33 – 14 = 19 On effectue des opérations arithmétiques pour résoudre le problème. | Je sais que Sylvia et Jacob ont le même nombre de poissons. 15 + 18 = 14 + □ Si Sylvia a 15 poissons rouges et Jacob en a 14, alors Jacob a 1 poisson rouge de moins que Sylvia. 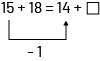 Puisque Jacob a le même nombre de poissons que Sylvia, il doit avoir 1 poisson à rayures jaunes de plus que Sylvia. 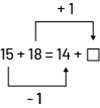 Donc □ = 19. Au lieu d’effectuer des calculs, on interprète le problème et on compare les quantités. On peut représenter la situation par une équation. Pour la résoudre, on compare les quantités de chaque côté du signe « = ». |
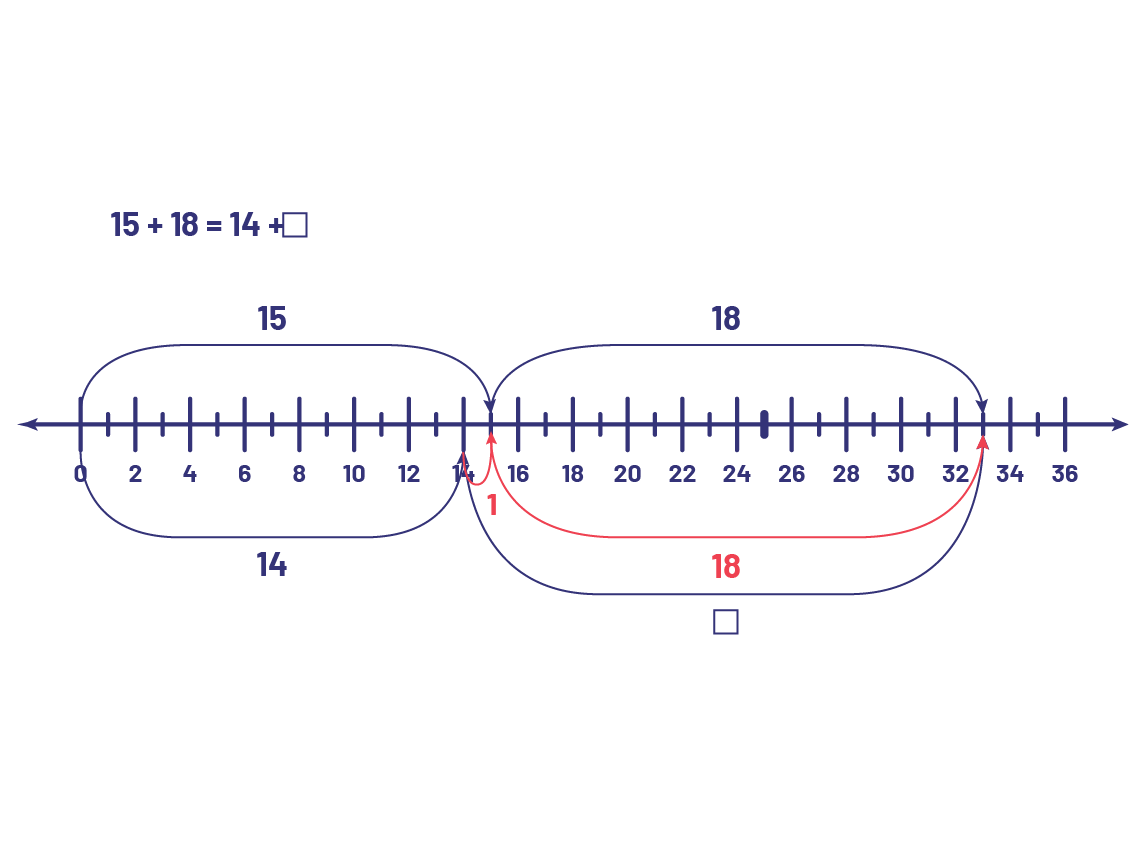
En général, les élèves ont tendance à résoudre un tel problème de façon arithmétique. Le personnel enseignant peut alors varier les paramètres du problème en lui donnant une perspective algébrique, par exemple, en demandant aux élèves de représenter la situation-problème à l’aide d’une équation. Pour résoudre l’équation, les élèves peuvent utiliser une droite numérique, ce qui peut les aider à réfléchir au calcul et non à faire le calcul. L’important n’est pas d’effectuer un calcul, mais de bien saisir la relation d’égalité entre les deux expressions numériques.
Habileté à communiquer un raisonnement algébrique
« La communication bénéficie à tous ceux qui participent à l’échange […]. L’obligation de faire part de sa compréhension d’une situation ou d’un concept contribue souvent à l’amélioration ou à l’approfondissement de cette compréhension. » (Ministère de l’Éducation du Québec, 2001, p. 132)
L’habileté à communiquer un raisonnement algébrique se développe lorsque les élèves expriment leur compréhension d’une situation-problème ou d’un concept, et défendent leurs idées en utilisant différents modes de représentation :
- le mode concret, lié à l’exploration, à la manipulation et à la création à l’aide de matériel concret;
- le mode semi-concret, lié à une illustration, à un dessin ou à toute autre représentation sur papier;
- le mode symbolique, lié à toute représentation faite à partir de chiffres ou de symboles;
- le mode « en mots », lié à une explication ou à une description verbale ou écrite.
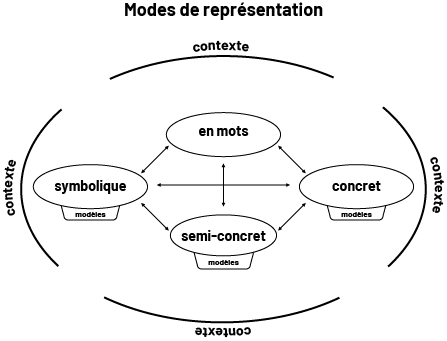
Afin d’acquérir une solide compréhension, les élèves doivent vivre des expériences en contexte en explorant des situations-problèmes. La mise en contexte permet aux élèves d’établir des liens entre diverses représentations et de développer une compréhension des concepts algébriques explorés. Le personnel enseignant utilise aussi diverses représentations afin d’aider les élèves à s’approprier les concepts mathématiques et à établir des liens entre les représentations.
L’argument mathématique est un outil essentiel de communication en mathématiques. Les élèves doivent parvenir à justifier leurs représentations, leurs idées et leur compréhension à l’aide d’arguments mathématiques, en se servant d’un vocabulaire de relations causales (par exemple, si… donc, parce que, puisque). Les arguments mathématiques permettent aux élèves de présenter leur compréhension de façon beaucoup plus juste et réfléchie. Pour plus de renseignements à ce sujet, consulter le document intitulé Communication et apprentissage : Repères conceptuels et pratiques pour la salle de classe de mathématiques (Radford et Demers, 2004, p. 15-25). Un argument mathématique est une justification orale ou écrite d’un raisonnement dans le but de démontrer ou de réfuter une idée mathématique.
L’échange mathématique est le moment idéal pour communiquer des représentations et des arguments mathématiques. Au moment de résoudre une situation-problème en algèbre, les élèves formulent des conjectures, présentent leurs pistes de solution, confrontent leurs idées ou justifient leurs résultats à l’aide de différentes représentations. Bref, les élèves communiquent.
Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 12-19.
Les composantes de l’apprentissage de l’algèbre sont les éléments fondamentaux que l’apprentissage en algèbre doit viser, peu importe l’année d’études (National Council of Teachers of Mathematics, 2000, p. 37-40). Ces composantes font partie de la toile de fond du programme-cadre. Ainsi, en algèbre, on doit reconnaître que l’on cherche à faire progresser les élèves dans leur apprentissage en les amenant à comprendre des relations, à utiliser des modèles mathématiques, à analyser le changement et à représenter des situations-problèmes à l’aide de symboles.
Chacune de ces composantes est abordée ci-après. Par la suite, on analyse une situation-problème de façon à illustrer l’intégration de ces composantes dans l’apprentissage en algèbre.
Compréhension des relations
Comprendre des relations est une habileté importante en résolution de problèmes en algèbre, puisqu’elle permet l’appropriation de concepts et la formulation de conjectures menant à des généralisations. Lorsque les élèves perçoivent et décrivent des régularités dans des suites, comparent, représentent et créent des situations ou des suites à partir de régularités, elles et ils cheminent vers l’établissement de relations entre des quantités.
Au cycle moyen, les élèves explorent des relations entre des quantités en changement, particulièrement dans des situations présentées par des suites croissantes. Pour développer leur sens du symbole, les élèves observent, analysent et représentent des nombres dans des phrases mathématiques et des équations.
Utilisation de modèles mathématiques
L’habileté à utiliser des modèles est une partie intégrante du programme-cadre de mathématiques. Les modèles mathématiques permettent de représenter des situations afin de pouvoir analyser les relations entre les nombres et les quantités. Au fil du temps, les spécialistes des mathématiques ont créé, utilisé et généralisé certaines idées, stratégies et représentations pour faciliter l’appropriation de concepts. À l’usage, certaines représentations sont devenues des modèles reconnus, par exemple la droite numérique et la disposition rectangulaire. Il est important que les élèves utilisent des modèles différents dans une variété d’activités pour pouvoir passer aisément d’une représentation à une autre.
Exemple
La multiplication 3 × 4 est ici représentée de trois façons différentes.
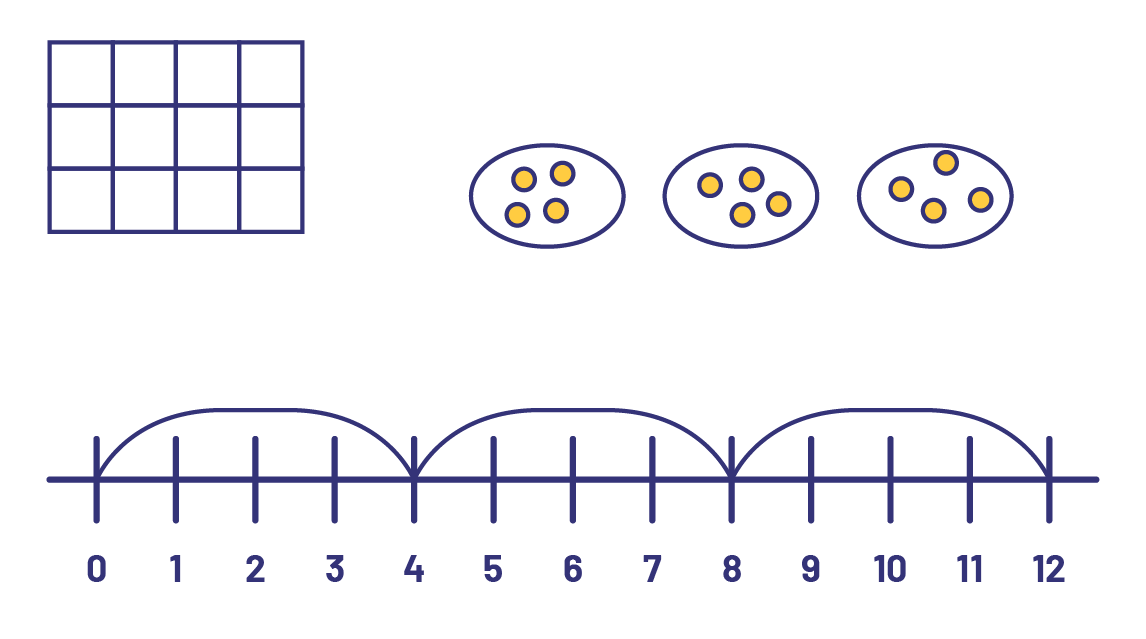 image Représentation de la multiplication de 3 fois 4 est représentée de trois manières différentes. 1ère façon : 3 carrés superposés répétés 4 fois. 2ème façon : 3 ensembles de 4 cercles jaunes à l'intérieur. 3e méthode : droite numérique avec des valeurs de zéro à 12, les flèches représentant les bonds de plus 4.
image Représentation de la multiplication de 3 fois 4 est représentée de trois manières différentes. 1ère façon : 3 carrés superposés répétés 4 fois. 2ème façon : 3 ensembles de 4 cercles jaunes à l'intérieur. 3e méthode : droite numérique avec des valeurs de zéro à 12, les flèches représentant les bonds de plus 4. Devant une situation-problème à résoudre, plusieurs représentations sont possibles; un certain nombre d’élèves utilisent leur corps, du matériel de manipulation ou des dessins, alors que d’autres représentent les données de façon plus schématique. La façon de s’approprier les données et de les organiser à l’aide de modèles reflète le degré de développement de la pensée algébrique.
Selon Fosnot et Dolk (2001), les modèles, à l’instar des grandes idées et des stratégies, ne peuvent pas être transmis par automatisme. Pour se les approprier, les élèves doivent les construire elles-mêmes et eux-mêmes. Puisque les élèves n’interprètent pas une situation de la même façon, il importe de leur soumettre des situations-problèmes qui favorisent la modélisation, de sorte qu’elles et ils puissent créer leurs propres symboles et leurs représentations personnelles. Il ne faut pas leur proposer systématiquement les algorithmes usuels ou les stratégies composées de règles et de conventions. Toutefois, certains modèles font partie intégrante des mathématiques et ils devront être explorés en classe dans un contexte plus structuré. La découverte de nouvelles représentations s’assimile à l’aide des trois apprentissages : communiqué, guidé et autonome.
Pour aider les élèves à raisonner, le personnel enseignant doit proposer une variété de modèles et de représentations, et inciter les élèves à les utiliser fréquemment.
En représentant une situation-problème, les élèves analysent les relations à l’aide de modèles, tirent des conclusions et les expliquent à l’aide de mots. Les modèles sont des outils qui aident à reconnaître les relations et à développer la pensée algébrique. Ils favorisent l’analyse et initient les élèves à un niveau d’abstraction qui facilite les prédictions et les généralisations. Le dialogue, l’échange mathématique sur les données du problème représenté par différents modèles, ainsi que les questions du personnel enseignant sont autant de moyens de susciter la réflexion chez les élèves.
Analyse du changement
Les élèves vivent dans un monde en changement. Comprendre que le changement fait partie de la vie, que la majorité des choses changent avec le temps (par exemple, chaque année pendant la période de croissance, la taille croît, le poids augmente, les pieds allongent) et que les changements peuvent être étudiés constitue une composante du développement de la pensée algébrique.
Les changements observés peuvent être décrits de façon qualitative (par exemple, je suis plus grande ou plus grand que l’an dernier, mes cheveux sont plus longs, le seau s’est rempli d’eau rapidement pendant l’orage, il fait plus froid que ce matin) ou de façon quantitative (par exemple, j’ai grandi de 2 cm cette année, le seau d’eau s’est rempli de 50 ml en 30 minutes, la température a chuté de 6 °C en 3 heures).
Les élèves apprennent à observer et à comprendre le changement dans les suites, dans les situations d’égalité et dans les situations-problèmes.
Le changement et les régularités sont deux concepts indissociables dans l’exploration des relations entre deux quantités en changement. Les élèves réalisent que le changement d’une quantité influe sur une autre. Par exemple, en observant la suite croissante ci-dessous, les élèves peuvent reconnaître le changement d’un rang à l’autre, soit que le nombre de carrés augmente d’un rang à l’autre. En poussant l’analyse du changement, les élèves peuvent reconnaître que le nombre de carrés double à chaque rang.
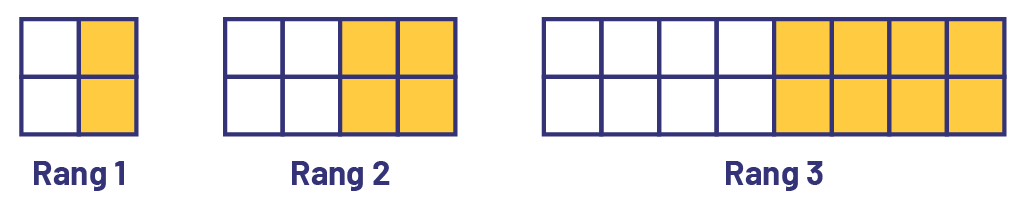 image Suite croissante non numérique avec des carrés. Rang un : 2 carrés blancs superposés et 2 carrés jaunes superposés. Rang 2 : 2 carrés blancs superposés répétés 2 fois et 2 carrés jaunes superposés répétés 2 fois. Rang 3 : 2 carrés blancs superposés répétés 4 fois et 2 carrés jaunes superposés répétés 4 fois.
image Suite croissante non numérique avec des carrés. Rang un : 2 carrés blancs superposés et 2 carrés jaunes superposés. Rang 2 : 2 carrés blancs superposés répétés 2 fois et 2 carrés jaunes superposés répétés 2 fois. Rang 3 : 2 carrés blancs superposés répétés 4 fois et 2 carrés jaunes superposés répétés 4 fois. Des élèves pourront même constater que le nombre de carrés qui composent une figure est égal à 2 × 2 × 2 × … × 2, où le nombre de multiplications est égal au rang de la figure.
L’étude d’une quantité en changement est un saut important dans la façon de voir les choses. Par exemple, dans un problème qui implique les longueurs de 5 cm, 7 cm, 9 cm…, au lieu de voir plusieurs quantités, on considère qu’il s’agit d’une seule longueur qui est en changement, d’où le besoin de faire intervenir le concept de la variable.
Représentation de situations-problèmes à l’aide de symboles
« Les symboles, surtout ceux dans les équations, sont une façon d’exprimer des généralisations qui expliquent des relations et des régularités. » [traduction libre] (Van de Walle et Folk, 2005, p. 401)
La représentation de situations-problèmes à l’aide de symboles est une composante fondamentale de la pensée algébrique. Il est important de faire cheminer les élèves vers une représentation plus abstraite et plus formelle des situations à l’aide de symboles; les élèves développent ainsi leur sens du symbole.
Exemple d’intégration des composantes dans une situation-problème
L’exemple ci-dessous illustre l’intégration des composantes de l’apprentissage de l’algèbre dans une situation-problème.
Dans la ville où Jessie et Boukar habitent, il y a deux centres d’entraînement physique, Méga et Extra, qui offrent des plans différents pour leurs membres.
Jessie va au centre d’entraînement Méga, où le coût de l’abonnement est de 25 $ et chaque cours coûte 2 $ chacun.
Boukar est abonné au centre d’entraînement Extra, où le coût de l’abonnement est de 4 $ et chaque cours coûte 5 $ chacun.
En te servant de ces renseignements, détermine à quel moment Jessie et Boukar auront déboursé la même somme d’argent pour un même nombre de cours.
Après avoir présenté le problème, le personnel enseignant pose des questions et invite les élèves à effectuer diverses tâches afin d’intégrer les composantes de l’apprentissage de l’algèbre.
Compréhension des relations
Le personnel enseignant fait ressortir les régularités et les relations en invitant les élèves à analyser la situation-problème et à la représenter d’une autre façon.
En général, les élèves relèvent qu’au centre d’entraînement Méga, la somme déboursée augmente de 2 $ chaque fois que Jessie prend part à un cours, tandis qu’au centre d’entraînement Extra, elle augmente de 5 $. En analysant davantage la situation, les élèves peuvent reconnaître qu’il y a une relation entre la somme déboursée et le nombre de cours à chaque centre d’entraînement.
Utiliser des modèles mathématiques
Voici quelques modèles qui peuvent être utilisés pour explorer cette situation-problème.
Droite numérique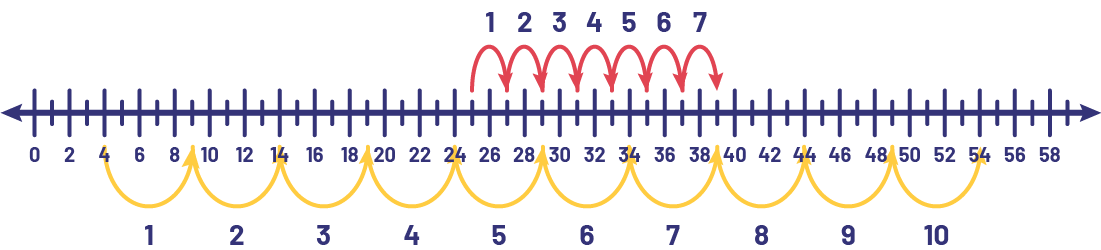 | ||||||||||||||||||||||||||||||||||||||||||||||||
Matériel de manipulation   | ||||||||||||||||||||||||||||||||||||||||||||||||
| Table de valeurs Centre d’entraînement Méga
Centre d’entraînement Extra
|
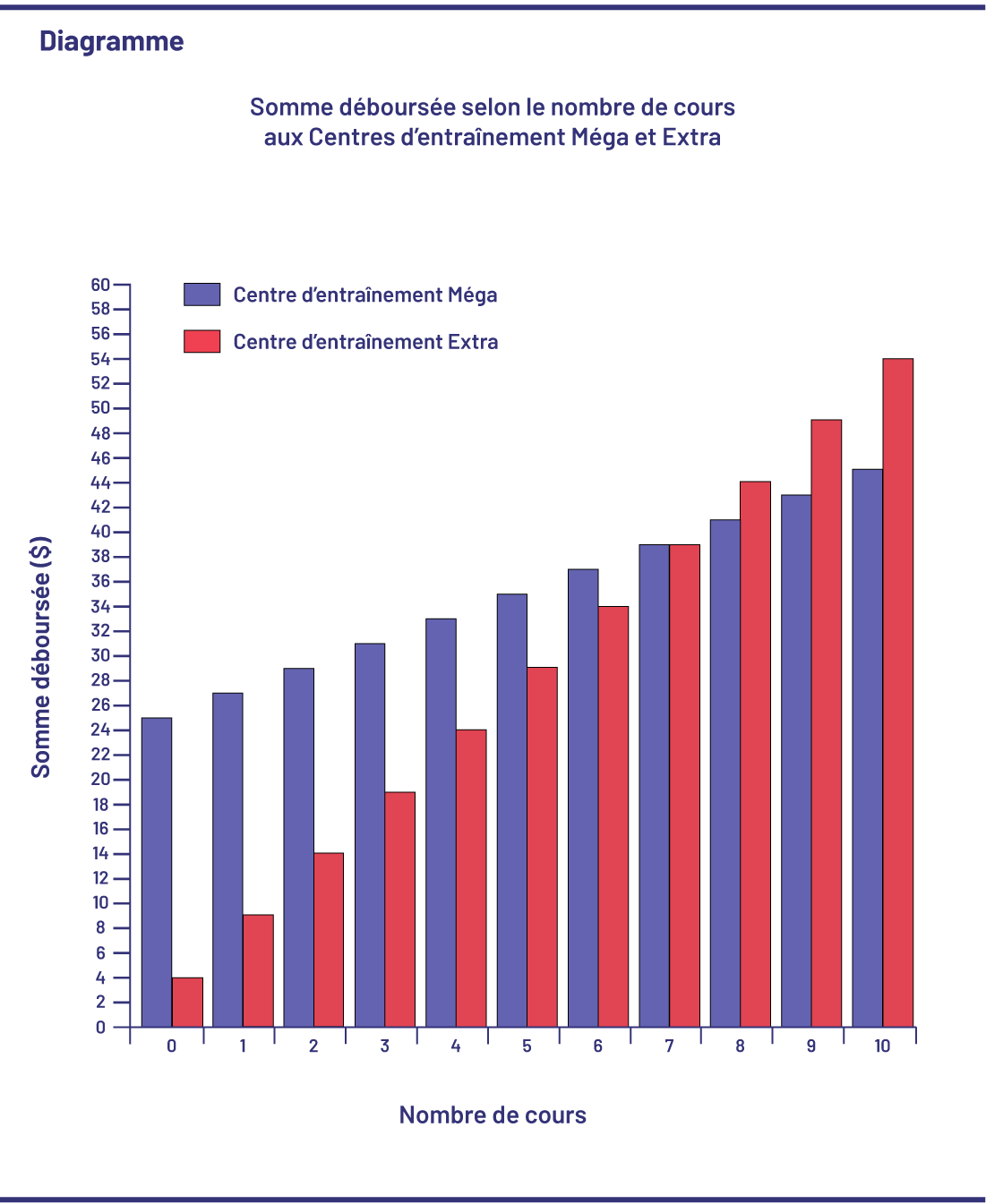
Analyser le changement
Voici quelques questions qui peuvent être posées afin d’analyser le changement dans cette situation-problème :
- Quelle information te permet de prédire (d’extrapoler) ce qui arrivera?
- Quelle étape ou quelles étapes doit-on répéter pour trouver la somme déboursée?
- Lorsque des nombres différents sont utilisés, qu’est-ce qui change? Qu’est-ce qui ne change pas?
- En quoi cette représentation (par exemple, avec le matériel de manipulation) ressemble-t-elle à celle-ci (par exemple, la table de valeurs)?
- Est-ce que cette démarche fonctionnerait toujours avec d’autres nombres? Comment le savez-vous?
Représenter des situations-problèmes à l’aide de symboles
En ayant recours à des interventions stratégiques, le personnel enseignant peut amener les élèves à représenter la situation en utilisant des symboles.
Exemples
Au centre d’entraînement Méga : s = 2 × c + 25, où s est la somme déboursée et c, le nombre de cours.
Au centre d’entraînement Extra : s = 5 × c + 4, où s est la somme déboursée et c, le nombre de cours.
Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 20-27.
Le personnel enseignant demeure le pivot de l’actualisation du développement de la pensée algébrique en salle de classe au cycle moyen. Son rôle ne se définit pas uniquement dans le choix des tâches, mais bien dans ses interventions qui visent à encourager les élèves à dépasser le raisonnement arithmétique et à accéder à un mode de pensée symbolique. Faire des mathématiques prend ainsi tout son sens.
Certains auteurs et auteures (par exemple, Blanton et Kaput, 2003, p. 70-77) croient que le personnel enseignant doit se munir « d’yeux et d’oreilles algébriques » afin de déterminer et de maximiser, dans les activités mathématiques, les liens avec les concepts algébriques et de saisir des occasions pour développer la pensée algébrique des élèves.
Pour ce faire, il peut :
Varier les paramètres d’un problème
Utiliser un problème existant et lui donner une perspective algébrique favorise la recherche de relations, de régularités, de conjectures et de généralisations.
Exemple de problème du domaine Nombres :
Dans une équipe de quatre personnes, combien de poignées de main y aura-t-il si chaque personne donne la main à toutes les autres personnes une seule fois?
À partir d’un problème de numération, le personnel enseignant pose des questions qui permettent de faire ressortir les liens avec les concepts algébriques, telles que :
- Combien y aura-t-il de poignées de main si une, deux ou trois autres personnes s’ajoutent à l’équipe?
- Organiser les données dans une table de valeurs. Est-ce que vous voyez une régularité?
- Combien de poignées de main y aura-t-il si dix personnes s’ajoutent à l’équipe?
Poser des questions pour aider les élèves à généraliser
- Que peut-on dire au sujet de la relation entre le nombre de personnes dans l’équipe et le nombre total de poignées de main?
- Y a-t-il une régularité? Expliquez votre réponse.
Poser des questions en mettant l’accent sur les concepts algébriques
- Pouvez-vous expliquer le problème dans vos mots?
- Pouvez-vous résoudre le problème à l’aide d’une autre représentation?
- Comment fait-on pour s’assurer que cette solution est vraie?
- Est-ce que cette démarche fonctionnerait avec d’autres nombres? Toujours?
- Qu’est-ce qui change?
- Qu’est-ce qui ne change pas?
Ces questions incitent les élèves à faire des conjectures et à les expliquer à l’aide d’arguments mathématiques.
Développer et renforcer une littératie des symboles
Le personnel enseignant doit initier les élèves à la littératie des symboles et les soutenir dans le développement de celle-ci. Trop souvent, l’application de plusieurs des symboles mathématiques se fait par automatisme, ces symboles étant perçus par des élèves simplement comme une commande d’exécution d’une opération mathématique. Ces élèves éprouvent alors des difficultés à résoudre un problème correctement et à expliquer ce que représente la phrase mathématique qu’elles et ils ont écrite, faute de compréhension des symboles qui la composent. Le travail du personnel enseignant consiste à mettre en place les stratégies qui permettent aux élèves :
- de lire les symboles et de réfléchir à ce qu’ils représentent avant d’agir;
- de comprendre la juste signification des symboles mathématiques (par exemple, le signe « = » représente une relation entre les expressions numériques de chaque côté du signe et n’est pas précurseur de la réponse);
- de reconnaître et d’utiliser les symboles comme outils de communication pour interpréter une phrase mathématique et pour exprimer son raisonnement.
Créer un milieu d’apprentissage « algébrique » : Un milieu d’apprentissage « algébrique » est un environnement où l’on mise sur le développement de la pensée analytique. Le personnel enseignant, de façon consciente, détermine et cerne des moments où le raisonnement fait partie intégrante de son enseignement. Argumenter, abstraire et généraliser devient pratique courante pendant des leçons quotidiennes en mathématiques et même dans les autres matières, et non un enrichissement occasionnel.
Créer un milieu d’apprentissage « algébrique », c’est donner la chance aux élèves de découvrir le monde qui les entoure avec des yeux et des oreilles « algébriques », c’est-à-dire d’être capables de généraliser de façon explicite.
Source : Guide d’enseignement efficace des mathématiques, de la maternelle à la 3e année, p. 23-24.

